7. B 14 . Пер­вый насос на­пол­ня­ет бак за 20 минут, вто­рой — за 30 минут, а тре­тий — за 1 час. За сколь­ко минут на­пол­нят бак три на­со­са, ра­бо­тая од­но­вре­мен­но?

Ре­ше­ние.

Обо­зна­чим объем бака за 1. Тогда три на­со­са, ра­бо­тая вме­сте, за­пол­нят бак за

 

минут.

Ответ: 10.

При­ве­дем дру­гое ре­ше­ние.

Пер­вый насос за ми­ну­ту на­пол­ня­ет одну два­дца­тую бака, вто­рой — одну трид­ца­тую, тре­тий — одну ше­сти­де­ся­тую. Ра­бо­тая вме­сте, за ми­ну­ту они на­пол­нят шесть ше­сти­де­ся­тых или одну де­ся­тую бака. Зна­чит, весь бак на­со­сы на­пол­нят за 10 минут.

 

При­ве­дем дру­гое ре­ше­ние.

За один час пер­вый насос на­пол­нит 3 бака, вто­рой — 2 бака, а тре­тий — 1 бак. Ра­бо­тая вме­сте, за один час они 6 баков. Зна­чит, один бак на­со­сы на­пол­нят в шесть раз быст­рее, т. е. за 10 минут.

Ответ: 10

8. B 14 . Улит­ка пол­зет от од­но­го де­ре­ва до дру­го­го. Каж­дый день она про­пол­за­ет на одно и то же рас­сто­я­ние боль­ше, чем в преды­ду­щий день. Из­вест­но, что за пер­вый и по­след­ний дни улит­ка про­полз­ла в общей слож­но­сти 10 мет­ров. Опре­де­ли­те, сколь­ко дней улит­ка по­тра­ти­ла на весь путь, если рас­сто­я­ние между де­ре­вья­ми равно 150 мет­рам.

Ре­ше­ние.

Пусть улит­ка про­полз­ла в пер­вый день мет­ров, во вто­рой – , … , в по­след­ний – мет­ров. Тогда м, а за дней про­полз­ла мет­ров. По­сколь­ку всего она про­полз­ла 150 мет­ров, имеем: . Таким об­ра­зом, улит­ка по­тра­ти­ла на весь путь 30 дней.

 

Ответ: 30.

Ответ: 30

9. B 14 . Поезд, дви­га­ясь рав­но­мер­но со ско­ро­стью 80 км/ч, про­ез­жа­ет мимо при­до­рож­но­го стол­ба за 36 се­кунд. Най­ди­те длину по­ез­да в мет­рах.

Ре­ше­ние.

Ско­рость по­ез­да равна . За 36 се­кунд поезд про­хо­дит мимо при­до­рож­но­го стол­ба рас­сто­я­ние, рав­ное своей длине:

 

.

Ответ: 800.

Ответ: 800

10. B 14 . Петя и Ваня вы­пол­ня­ют оди­на­ко­вый тест. Петя от­ве­ча­ет за час на 8 во­про­сов тек­ста, а Ваня – на 9. Они од­но­вре­мен­но на­ча­ли от­ве­чать на во­про­сы теста, и Петя за­кон­чил свой тест позже Вани на 20 минут. Сколь­ко во­про­сов со­дер­жит тест?

Вариант № 3715666

1. B 14 . Ви­но­град со­дер­жит 90% влаги, а изюм — 5%. Сколь­ко ки­ло­грам­мов ви­но­гра­да тре­бу­ет­ся для по­лу­че­ния 20 ки­ло­грам­мов изюма?

Ре­ше­ние.

Ви­но­град со­дер­жит 10% пи­та­тель­но­го ве­ще­ства, а изюм — 95%. По­это­му 20 кг изюма со­дер­жат кг пи­та­тель­но­го ве­ще­ства. Таким об­ра­зом, для по­лу­че­ния 20 ки­ло­грам­мов изюма тре­бу­ет­ся кг ви­но­гра­да.

 

Ответ: 190.

Ответ: 190

2. B 14 . Два че­ло­ве­ка от­прав­ля­ют­ся из од­но­го и того же места на про­гул­ку до опуш­ки леса, на­хо­дя­щей­ся в 4,4 км от места от­прав­ле­ния. Один идёт со ско­ро­стью 2,5 км/ч, а дру­гой — со ско­ро­стью 3 км/ч. Дойдя до опуш­ки, вто­рой с той же ско­ро­стью воз­вра­ща­ет­ся об­рат­но. На каком рас­сто­я­нии от точки от­прав­ле­ния про­изойдёт их встре­ча?

Ре­ше­ние.

Пусть x ч — время, про­шед­шее от на­ча­ла дви­же­ния до мо­мен­та встре­чи пе­ше­хо­дов. Тогда к мо­мен­ту их встре­чи тот, кто шёл мед­лен­нее, прошёл 2,5x км, а тот, кто шёл быст­рее, прошёл 4,4 км до опуш­ки и ещё 3x км в об­рат­ном на­прав­ле­нии. Пе­ше­хо­ды встре­ти­лись на одном и том же рас­сто­я­нии от опуш­ки, по­это­му рас­сто­я­ние, ко­то­рое ещё оста­лось прой­ти до опуш­ки более мед­лен­но­му из них, равно рас­сто­я­нию, на ко­то­рое более быст­рый от неё уже уда­лил­ся. Сле­до­ва­тель­но, 4,4 − 2,5х = 3х − 4,4, от­ку­да х = 1,6 ч, а ис­ко­мое рас­сто­я­ние равно 2,5 · 1,8 = 4 км.

 

При­ве­дем дру­гое ре­ше­ние.

Тот, кто идет быст­рее, дой­дет до опуш­ки за 4,4 : 3 = 22/15 часа. За это время тот, кто идет мед­лен­нее, прой­дет 2,5 · 22/15 = 11/3 км и ока­жет­ся на рас­сто­я­нии 4,4 − 11/3 = 11/15 км от опуш­ки. Далее они пой­дут на встре­чу друг другу со ско­ро­стью сбли­же­ния 5,5 км/час и пре­одо­ле­ют раз­де­ля­ю­щее их рас­сто­я­ние за (11/15) : 5,5 = 2/15 часа. За это время мед­лен­но иду­щий пе­ше­ход прой­дет еще 2,5 · 2/15 = 1/3 км и ока­жет­ся на рас­сто­я­нии 11/3 + 1/3 = 4 км от точки от­прав­ле­ния.

Ответ: 4.

Ответ: 4

3. B 14 . Пер­вый ве­ло­си­пе­дист вы­ехал из по­сел­ка по шоссе со ско­ро­стью 15 км/ч. Через час после него со ско­ро­стью 10 км/ч из того же по­сел­ка в том же на­прав­ле­нии вы­ехал вто­рой ве­ло­си­пе­дист, а еще через час после этого – тре­тий. Най­ди­те ско­рость тре­тье­го ве­ло­си­пе­ди­ста, если сна­ча­ла он до­гнал вто­ро­го, а через 2 часа 20 минут после этого до­гнал пер­во­го. Ответ дайте в км/ч.

Ре­ше­ние.

Пусть км/ч – ско­рость тре­тье­го ве­ло­си­пе­ди­ста, а ч – время, ко­то­рое по­на­до­би­лось ему, чтобы до­гнать вто­ро­го ве­ло­си­пе­ди­ста. Таким об­ра­зом,

 

.

А через 2 часа 20 минут после этого до­гнал пер­во­го. Таким об­ра­зом,

 

Таким об­ра­зом, .

Ответ: 25.

Ответ: 25

4. B 14 . Сме­ша­ли не­ко­то­рое ко­ли­че­ство 15–про­цент­но­го рас­тво­ра не­ко­то­ро­го ве­ще­ства с таким же ко­ли­че­ством 19–про­цент­но­го рас­тво­ра этого ве­ще­ства. Сколь­ко про­цен­тов со­став­ля­ет кон­цен­тра­ция по­лу­чив­ше­го­ся рас­тво­ра?

Ре­ше­ние.

Кон­цен­тра­ция рас­тво­ра равна . Пусть объем по­лу­чив­ше­го­ся рас­тво­ра лит­ров. Таким об­ра­зом, кон­цен­тра­ция по­лу­чен­но­го рас­тво­ра равна:

 

Ответ: 17.

Ответ: 17

5. B 14 . Из пунк­та A кру­го­вой трас­сы вы­ехал ве­ло­си­пе­дист, а через 30 минут сле­дом за ним от­пра­вил­ся мо­то­цик­лист. Через 10 минут после от­прав­ле­ния он до­гнал ве­ло­си­пе­ди­ста в пер­вый раз, а еще через 30 минут после этого до­гнал его во вто­рой раз. Най­ди­те ско­рость мо­то­цик­ли­ста, если длина трас­сы равна 30 км. Ответ дайте в км/ч.

Ре­ше­ние.

К мо­мен­ту пер­во­го об­го­на мо­то­цик­лист за 10 минут про­ехал столь­ко же, сколь­ко ве­ло­си­пе­дист за 40 минут, сле­до­ва­тель­но, его ско­рость в 4 раза боль­ше. По­это­му, если ско­рость ве­ло­си­пе­ди­ста при­нять за x км/час, то ско­рость мо­то­цик­ли­ста будет равна 4x, а ско­рость их сбли­же­ния — 3x км/час.

 

C дру­гой сто­ро­ны, вто­рой раз мо­то­цик­лист до­гнал ве­ло­си­пе­ди­ста за 30 минут, за это время он про­ехал на 30 км боль­ше. Сле­до­ва­тель­но, ско­рость их сбли­же­ния со­став­лят 60 км/час.

 

Итак, 3х = 60 км/час, от­ку­да ско­рость ве­ло­си­пе­ди­ста равна 20 км/час, а ско­рость мо­то­цик­ли­ста равна 80 км/час.

Ответ: 80

6. B 14 . До­ро­га между пунк­та­ми А и В со­сто­ит из подъёма и спус­ка, а её длина равна 8 км. Пе­ше­ход прошёл путь из А в В за 2 часа 45 минут. Время его дви­же­ния на спус­ке со­ста­ви­ло 1 час 15 минут. С какой ско­ро­стью пе­ше­ход шёл на спус­ке, если ско­рость его дви­же­ния на подъёме мень­ше ско­ро­сти дви­же­ния на спус­ке на 2 км/ч? Ответ вы­ра­зи­те в км/ч.

Ре­ше­ние.

За­ме­тим, что время подъ­ема со­ста­ви­ло 1 час 30 минут или 1,5 часа, а время спус­ка 1,25 часа. Пусть x км/ч — ско­рость дви­же­ния пе­ше­хо­да на спус­ке, тогда х − 2 км/ч — ско­рость дви­же­ния пе­ше­хо­да на подъ­еме, 1,25х км — длина пути на спус­ке, 1,5(х − 2) км — длина пути на подъ­еме. Всего было прой­де­но 8 км, от­ку­да имеем:

 

 

Тем самым, ско­рость пе­ше­хо­да на спус­ке была равна 4 км/ч.

 

Ответ: 4.

Ответ: 4

7. B 14 . Рас­сто­я­ние между при­ста­ня­ми и равно 120 км. Из в по те­че­нию реки от­пра­вил­ся плот, а через час вслед за ним от­пра­ви­лась яхта, ко­то­рая, при­быв в пункт , тот­час по­вер­ну­ла об­рат­но и воз­вра­ти­лась в . К этому вре­ме­ни плот про­шел 24 км. Най­ди­те ско­рость яхты в не­по­движ­ной воде, если ско­рость те­че­ния реки равна 2 км/ч. Ответ дайте в км/ч.

Ре­ше­ние.

Ско­рость плота равна ско­ро­сти те­че­ния реки 2 км/ч. Пусть км/ч – ско­рость яхты, тогда ско­рость яхты по те­че­нию равна км/ч, а ско­рость яхты про­тив те­че­ния равна км/ч. Яхта, при­быв в пункт , тот­час по­вер­ну­ла об­рат­но и воз­вра­ти­лась в , а плоту по­на­до­би­лось на час боль­ше вре­ме­ни, чтобы прой­ти 24 км.

 

Ответ: 22.

Ответ: 22

8. B 14 . То­вар­ный поезд каж­дую ми­ну­ту про­ез­жа­ет на 750 мет­ров мень­ше, чем ско­рый, и на путь в 180 км тра­тит вре­ме­ни на 2 часа боль­ше, чем ско­рый. Най­ди­те ско­рость то­вар­но­го по­ез­да. Ответ дайте в км/ч.

Ре­ше­ние.

Ско­рость то­вар­но­го по­ез­да мень­ше, чем ско­ро­го на 750 м/мин или на

 

.

Пусть км/ч — ско­рость то­вар­но­го по­ез­да, тогда ско­рость ско­ро­го по­ез­да км/ч. На путь в 180 км то­вар­ный поезд тра­тит вре­ме­ни на 2 часа боль­ше, чем ско­рый, от­сю­да имеем:

 

Ответ: 45.

Ответ: 45

9. B 14 . Мо­тор­ная лодка в 10:00 вышла из пунк­та в пункт , рас­по­ло­жен­ный в 30 км от . Про­быв в пунк­те часа 30 минут, лодка от­пра­ви­лась назад и вер­ну­лась в пункт в 18:00. Опре­де­ли­те (в км/ч) соб­ствен­ную ско­рость лодки, если из­вест­но, что ско­рость те­че­ния реки 1 км/ч.

Ре­ше­ние.

Пусть км/ч — соб­ствен­ная ско­рость мо­тор­ной лодки, тогда ско­рость лодки по те­че­нию равна км/ч, а ско­рость лодки про­тив те­че­ния равна км/ч. На весь путь лодка за­тра­ти­ла (часов), от­сю­да имеем:

 

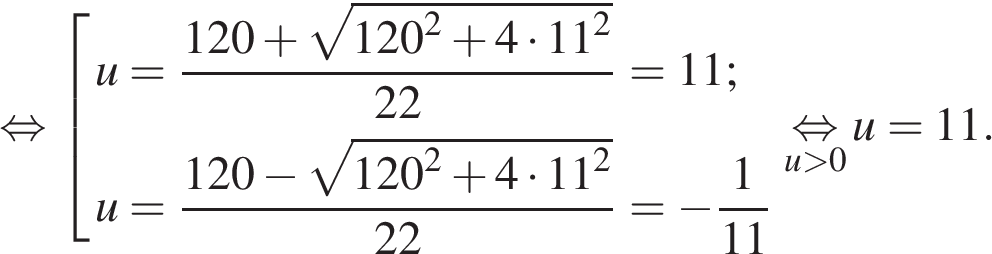
Таким об­ра­зом соб­ствен­ная ско­рость лодки равна 11 км/ч.

Ответ: 11.

Ответ: 11

10. B 14 . Два гон­щи­ка участ­ву­ют в гон­ках. Им пред­сто­ит про­ехать 60 кру­гов по коль­це­вой трас­се про­тяжённо­стью 3 км. Оба гон­щи­ка стар­то­ва­ли од­но­вре­мен­но, а на финиш пер­вый пришёл рань­ше вто­ро­го на 10 минут. Чему рав­ня­лась сред­няя ско­рость вто­ро­го гон­щи­ка, если из­вест­но, что пер­вый гон­щик в пер­вый раз обо­гнал вто­ро­го на круг через 15 минут?