Вариант № 3715436

1. B 14 . Часы со стрел­ка­ми по­ка­зы­ва­ют 3 часа ровно. Через сколь­ко минут ми­нут­ная стрел­ка в де­вя­тый раз по­рав­ня­ет­ся с ча­со­вой?

Ре­ше­ние.

Ско­рость дви­же­ния ми­нут­ной стрел­ки 12 де­ле­ний/час (под одним де­ле­ни­ем здесь под­ра­зу­ме­ва­ет­ся рас­сто­я­ние между со­сед­ни­ми циф­ра­ми на ци­фер­бла­те часов), а ча­со­вой – 1 де­ле­ние/час. До де­вя­той встре­чи ми­нут­ной и ча­со­вой стре­лок ми­нут­ная долж­на сна­ча­ла 8 раз «обо­гнать» ча­со­вую, то есть прой­ти 8 кру­гов по 12 де­ле­ний. Пусть после этого до по­след­ней встре­чи ча­со­вая стрел­ка прой­дет де­ле­ний. Тогда общий путь ми­нут­ной стрел­ки скла­ды­ва­ет­ся из най­ден­ных 96 де­ле­ний, ещё 3 из­на­чаль­но раз­де­ля­ю­щих их де­ле­ний (по­сколь­ку часы по­ка­зы­ва­ют 3 часа) и по­след­них L де­ле­ний. При­рав­ня­ем время дви­же­ния для ча­со­вой и ми­нут­ной стре­лок:

 

.

 

Ча­со­вая стрел­ка прой­дет 9 де­ле­ний, что со­от­вет­ству­ет 9 часам или 540 ми­ну­там.

 

Ответ: 540.

 

 

По прось­бам чи­та­те­лей по­ме­ща­ем общее ре­ше­ние.

Ско­рость вра­ще­ния ча­со­вой стрел­ки равна 0,5 гра­ду­са в ми­ну­ту, а ми­нут­ной — 6 гра­ду­сов в ми­ну­ту. По­это­му когда часы по­ка­зы­ва­ют время h часов m минут ча­со­вая стрел­ка по­вер­ну­та на 30h + 0,5m гра­ду­сов, а ми­нут­ная — на 6m гра­ду­сов от­но­си­тель­но 12-ча­со­во­го де­ле­ния.

Пусть в пер­вый раз стрел­ки встре­тят­ся через t₁ минут. Тогда если ми­нут­ная стрел­ка еще не опе­ре­жа­ла ча­со­вую в те­че­ние те­ку­ще­го часа, то 6m + 6t₁ = 30h + 0,5m + 0,5t₁, т. е. t₁ = (60h − 11m)/11 (*). В про­ти­во­по­лож­ном слу­чае по­лу­ча­ем урав­не­ние 6m + 6t₁ = 30h + 0,5m + 0,5t₁ + 360, от­ку­да t₁ = (60h − 11m + 720)/11 (**).

Пусть во вто­рой раз стрел­ки встре­тят­ся через t₂ минут после пер­во­го, тогда 0,5t₂ = 6t₂ − 360, от­ку­да t₂ = 720/11 (***). Это же верно для каж­до­го сле­ду­ю­ще­го обо­ро­та.

По­это­му для встре­чи с но­ме­ром n из (*) и (**) с уче­том (***) имеем со­от­вет­ствен­но: t_n = (60h − 11m + 720(n − 1))/11 или t_n = (60h − 11m + 720n)/11.

Ответ: 540

2. B 14 . Име­ет­ся два спла­ва. Пер­вый сплав со­дер­жит 10% ни­ке­ля, вто­рой – 30% ни­ке­ля. Из этих двух спла­вов по­лу­чи­ли тре­тий сплав мас­сой 200 кг, со­дер­жа­щий 25% ни­ке­ля. На сколь­ко ки­ло­грам­мов масса пер­во­го спла­ва мень­ше массы вто­ро­го?

Ре­ше­ние.

Пусть масса пер­во­го спла­ва кг, а масса вто­ро­го – кг. Тогда мас­со­вое со­дер­жа­ние ни­ке­ля в пер­вом и вто­ром спла­вах и , со­от­вет­ствен­но. Из этих двух спла­вов по­лу­чи­ли тре­тий сплав мас­сой 200 кг, со­дер­жа­щий 25% ни­ке­ля. По­лу­ча­ем си­сте­му урав­не­ний:

 

Таким об­ра­зом, пер­вый сплав легче вто­ро­го на 100 ки­ло­грам­мов.

 

Ответ: 100.

Ответ: 100

3. B 14 . Два ве­ло­си­пе­ди­ста од­но­вре­мен­но от­пра­ви­лись в 240-ки­ло­мет­ро­вый про­бег. Пер­вый ехал со ско­ро­стью, на 1 км/ч боль­шей, чем ско­рость вто­ро­го, и при­был к фи­ни­шу на 1 час рань­ше вто­ро­го. Найти ско­рость ве­ло­си­пе­ди­ста, при­шед­ше­го к фи­ни­шу пер­вым. Ответ дайте в км/ч.

Ре­ше­ние.

Пусть км/ч — ско­рость ве­ло­си­пе­ди­ста, при­шед­ше­го к фи­ни­шу пер­вым, тогда ско­рость вто­ро­го ве­ло­си­пе­ди­ста — км/ч, . Пер­вый ве­ло­си­пе­дист при­был к фи­ни­шу на 1 час рань­ше вто­ро­го, от­сю­да имеем:

 

Зна­чит, пер­вым фи­ни­ши­ро­вал ве­ло­си­пе­дист, дви­гав­ший­ся со ско­ро­стью 16 км/ч.

Ответ: 16.

Ответ: 16

4. B 14 . По двум па­рал­лель­ным же­лез­но­до­рож­ным путям друг нав­стре­чу другу сле­ду­ют ско­рый и пас­са­жир­ский по­ез­да, ско­ро­сти ко­то­рых равны со­от­вет­ствен­но 65 км/ч и 35 км/ч. Длина пас­са­жир­ско­го по­ез­да равна 700 мет­рам. Най­ди­те длину ско­ро­го по­ез­да, если время, за ко­то­рое он про­шел мимо пас­са­жир­ско­го по­ез­да, равно 36 се­кун­дам. Ответ дайте в мет­рах.

Ре­ше­ние.

От­но­си­тель­ная ско­рость по­ез­дов равна

 

За 36 се­кунд один поезд про­хо­дит мимо дру­го­го, то есть вме­сте по­ез­да пре­одо­ле­ва­ют рас­сто­я­ние, рав­ное сумме их длин:

 

м,

по­это­му длина ско­ро­го по­ез­да

Ответ: 300.

Ответ: 300

5. B 14 . Ве­ло­си­пе­дист вы­ехал с по­сто­ян­ной ско­ро­стью из го­ро­да A в город B, рас­сто­я­ние между ко­то­ры­ми равно 70 км. На сле­ду­ю­щий день он от­пра­вил­ся об­рат­но в A со ско­ро­стью на 3 км/ч боль­ше преж­ней. По до­ро­ге он сде­лал оста­нов­ку на 3 часа. В ре­зуль­та­те ве­ло­си­пе­дист за­тра­тил на об­рат­ный путь столь­ко же вре­ме­ни, сколь­ко на путь из A в B. Най­ди­те ско­рость ве­ло­си­пе­ди­ста на пути из B в A. Ответ дайте в км/ч.

Ре­ше­ние.

Пусть км/ч – ско­рость ве­ло­си­пе­ди­ста на пути из B в A, тогда ско­рость ве­ло­си­пе­ди­ста на пути из A в B равна  км/ч. Сде­лав на об­рат­ном пути оста­нов­ку на 3 часа, ве­ло­си­пе­дист за­тра­тил на об­рат­ный путь столь­ко же вре­ме­ни, сколь­ко на путь из A в B, от­сю­да имеем:

 

 

Таким об­ра­зом, ско­рость ве­ло­си­пе­ди­ста была равна 10 км/ч.

Ответ: 10.

Ответ: 10

6. B 14 . До­ро­га между пунк­та­ми А и В со­сто­ит из подъёма и спус­ка, а её длина равна 8 км. Пе­ше­ход прошёл путь из А в В за 2 часа 45 минут. Время его дви­же­ния на спус­ке со­ста­ви­ло 1 час 15 минут. С какой ско­ро­стью пе­ше­ход шёл на спус­ке, если ско­рость его дви­же­ния на подъёме мень­ше ско­ро­сти дви­же­ния на спус­ке на 2 км/ч? Ответ вы­ра­зи­те в км/ч.

Ре­ше­ние.

За­ме­тим, что время подъ­ема со­ста­ви­ло 1 час 30 минут или 1,5 часа, а время спус­ка 1,25 часа. Пусть x км/ч — ско­рость дви­же­ния пе­ше­хо­да на спус­ке, тогда х − 2 км/ч — ско­рость дви­же­ния пе­ше­хо­да на подъ­еме, 1,25х км — длина пути на спус­ке, 1,5(х − 2) км — длина пути на подъ­еме. Всего было прой­де­но 8 км, от­ку­да имеем:

 

 

Тем самым, ско­рость пе­ше­хо­да на спус­ке была равна 4 км/ч.

 

Ответ: 4.

Ответ: 4

7. B 14 . Гру­зо­вик пе­ре­во­зит пар­тию щебня мас­сой 60 тонн, еже­днев­но уве­ли­чи­вая норму пе­ре­воз­ки на одно и то же число тонн. Из­вест­но, что за пер­вый день было пе­ре­ве­зе­но 4 тонны щебня. Опре­де­ли­те, сколь­ко тонн щебня было пе­ре­ве­зе­но за пятый день, если вся ра­бо­та была вы­пол­не­на за 8 дней.

Ре­ше­ние.

Пусть в пер­вый день гру­зо­вик пе­ре­вез тонны щебня, во вто­рой — , …, в по­след­ний — тонн; всего было пе­ре­ве­зе­но тонн; норма пе­ре­воз­ки уве­ли­чи­ва­лась еже­днев­но на тонн. По­сколь­ку

 

.

Имеем

 

.

Сле­до­ва­тель­но, за пятый день было пе­ре­ве­зе­но 8 тонн щебня.

Ответ: 8.

Ответ: 8

8. B 14 . Име­ют­ся два со­су­да. Пер­вый со­дер­жит 30 кг, а вто­рой – 20 кг рас­тво­ра кис­ло­ты раз­лич­ной кон­цен­тра­ции. Если эти рас­тво­ры сме­шать, то по­лу­чит­ся рас­твор, со­дер­жа­щий 68% кис­ло­ты. Если же сме­шать рав­ные массы этих рас­тво­ров, то по­лу­чит­ся рас­твор, со­дер­жа­щий 70% кис­ло­ты. Сколь­ко ки­ло­грам­мов кис­ло­ты со­дер­жит­ся в пер­вом со­су­де?

Ре­ше­ние.

Пусть кон­цен­тра­ция пер­во­го рас­тво­ра кис­ло­ты – , а кон­цен­тра­ция вто­ро­го – . Если сме­шать эти рас­тво­ры кис­ло­ты, то по­лу­чит­ся рас­твор, со­дер­жа­щий 68% кис­ло­ты: . Если же сме­шать рав­ные массы этих рас­тво­ров, то по­лу­чит­ся рас­твор, со­дер­жа­щий 70% кис­ло­ты: . Решим по­лу­чен­ную си­сте­му урав­не­ний:

 

По­это­му

Ответ: 18.

Ответ: 18

9. B 14 . Двое ра­бо­чих, ра­бо­тая вме­сте, могут вы­пол­нить ра­бо­ту за 12 дней. За сколь­ко дней, ра­бо­тая от­дель­но, вы­пол­нит эту ра­бо­ту пер­вый ра­бо­чий, если он за два дня вы­пол­ня­ет такую же часть ра­бо­ты, какую вто­рой – за три дня?

Ре­ше­ние.

Обо­зна­чим и – объёмы работ, ко­то­рые вы­пол­ня­ют за день пер­вый и вто­рой ра­бо­чий, со­от­вет­ствен­но, пол­ный объём работ при­мем за 1. Тогда по усло­вию за­да­чи и . Решим по­лу­чен­ную си­сте­му:

 

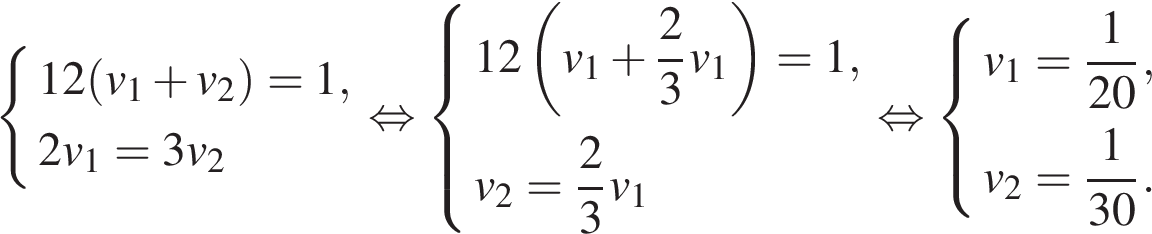
Тем самым, пер­вый ра­бо­чий за день вы­пол­ня­ет одну два­дца­тую всей ра­бо­ты, зна­чит, ра­бо­тая от­дель­но, он спра­вит­ся с ней за 20 дней.

Ответ: 20.

Ответ: 20

10. B 14 . В сосуд, со­дер­жа­щий 5 лит­ров 12–про­цент­но­го вод­но­го рас­тво­ра не­ко­то­ро­го ве­ще­ства, до­ба­ви­ли 7 лит­ров воды. Сколь­ко про­цен­тов со­став­ля­ет кон­цен­тра­ция по­лу­чив­ше­го­ся рас­тво­ра?