Задание В14

Вариант № 3714834

1. B 14 . Пер­вый насос на­пол­ня­ет бак за 20 минут, вто­рой — за 30 минут, а тре­тий — за 1 час. За сколь­ко минут на­пол­нят бак три на­со­са, ра­бо­тая од­но­вре­мен­но?

Ре­ше­ние.

Обо­зна­чим объем бака за 1. Тогда три на­со­са, ра­бо­тая вме­сте, за­пол­нят бак за

 

минут.

Ответ: 10.

При­ве­дем дру­гое ре­ше­ние.

Пер­вый насос за ми­ну­ту на­пол­ня­ет одну два­дца­тую бака, вто­рой — одну трид­ца­тую, тре­тий — одну ше­сти­де­ся­тую. Ра­бо­тая вме­сте, за ми­ну­ту они на­пол­нят шесть ше­сти­де­ся­тых или одну де­ся­тую бака. Зна­чит, весь бак на­со­сы на­пол­нят за 10 минут.

 

При­ве­дем дру­гое ре­ше­ние.

За один час пер­вый насос на­пол­нит 3 бака, вто­рой — 2 бака, а тре­тий — 1 бак. Ра­бо­тая вме­сте, за один час они 6 баков. Зна­чит, один бак на­со­сы на­пол­нят в шесть раз быст­рее, т. е. за 10 минут.

Ответ: 10

2. B 14 . Пер­вый сплав со­дер­жит 10% меди, вто­рой – 40% меди. Масса вто­ро­го спла­ва боль­ше массы пер­во­го на 3 кг. Из этих двух спла­вов по­лу­чи­ли тре­тий сплав, со­дер­жа­щий 30% меди. Най­ди­те массу тре­тье­го спла­ва. Ответ дайте в ки­ло­грам­мах.

Ре­ше­ние.

Пусть масса пер­во­го спла­ва кг, а масса вто­ро­го – кг, масса тре­тье­го спла­ва – кг. Пер­вый сплав со­дер­жит 10% меди, вто­рой – 40% меди, тре­тий сплав – 30% меди. Тогда:

 

Ответ: 9.

Ответ: 9

3. B 14 . На из­го­тов­ле­ние 99 де­та­лей пер­вый ра­бо­чий тра­тит на 2 часа мень­ше, чем вто­рой ра­бо­чий на из­го­тов­ле­ние 110 таких же де­та­лей. Из­вест­но, что пер­вый ра­бо­чий за час де­ла­ет на 1 де­таль боль­ше, чем вто­рой. Сколь­ко де­та­лей в час де­ла­ет вто­рой ра­бо­чий?

Ре­ше­ние.

Обо­зна­чим — число де­та­лей, ко­то­рые из­го­тав­ли­ва­ет за час вто­рой ра­бо­чий. Тогда пер­вый ра­бо­чий за час из­го­тав­ли­ва­ет де­таль. На из­го­тов­ле­ние 99 де­та­лей пер­вый ра­бо­чий тра­тит на 2 часа мень­ше, чем вто­рой ра­бо­чий на из­го­тов­ле­ние 110 таких же де­та­лей, от­сю­да имеем:

 

.

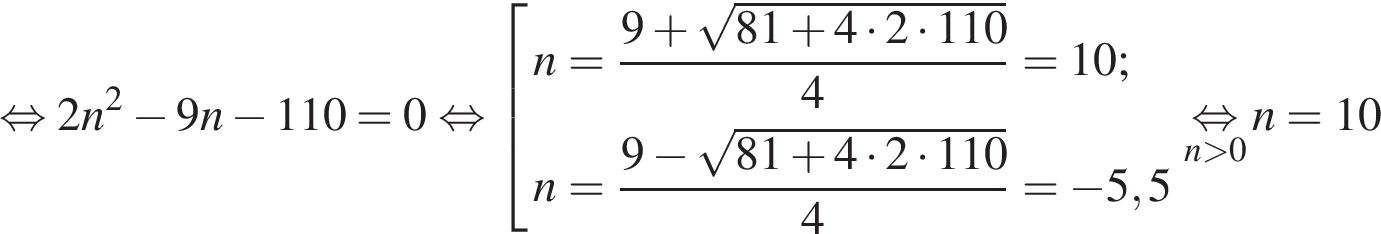Таким об­ра­зом, вто­рой ра­бо­чий де­ла­ет 10 де­та­лей в час.

Ответ: 10.

Ответ: 10

4. B 14 . Пер­вый ве­ло­си­пе­дист вы­ехал из по­сел­ка по шоссе со ско­ро­стью 15 км/ч. Через час после него со ско­ро­стью 10 км/ч из того же по­сел­ка в том же на­прав­ле­нии вы­ехал вто­рой ве­ло­си­пе­дист, а еще через час после этого – тре­тий. Най­ди­те ско­рость тре­тье­го ве­ло­си­пе­ди­ста, если сна­ча­ла он до­гнал вто­ро­го, а через 2 часа 20 минут после этого до­гнал пер­во­го. Ответ дайте в км/ч.

Ре­ше­ние.

Пусть км/ч – ско­рость тре­тье­го ве­ло­си­пе­ди­ста, а ч – время, ко­то­рое по­на­до­би­лось ему, чтобы до­гнать вто­ро­го ве­ло­си­пе­ди­ста. Таким об­ра­зом,

 

.

А через 2 часа 20 минут после этого до­гнал пер­во­го. Таким об­ра­зом,

 

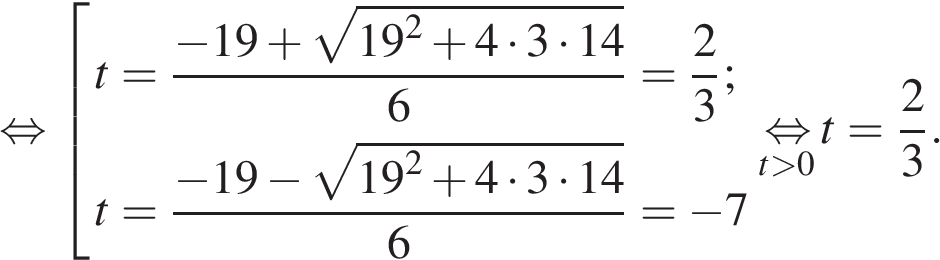
Таким об­ра­зом, .

Ответ: 25.

Ответ: 25

5. B 14 . Два че­ло­ве­ка от­прав­ля­ют­ся из од­но­го и того же места на про­гул­ку до опуш­ки леса, на­хо­дя­щей­ся в 4,4 км от места от­прав­ле­ния. Один идёт со ско­ро­стью 2,5 км/ч, а дру­гой — со ско­ро­стью 3 км/ч. Дойдя до опуш­ки, вто­рой с той же ско­ро­стью воз­вра­ща­ет­ся об­рат­но. На каком рас­сто­я­нии от точки от­прав­ле­ния про­изойдёт их встре­ча?

Ре­ше­ние.

Пусть x ч — время, про­шед­шее от на­ча­ла дви­же­ния до мо­мен­та встре­чи пе­ше­хо­дов. Тогда к мо­мен­ту их встре­чи тот, кто шёл мед­лен­нее, прошёл 2,5x км, а тот, кто шёл быст­рее, прошёл 4,4 км до опуш­ки и ещё 3x км в об­рат­ном на­прав­ле­нии. Пе­ше­хо­ды встре­ти­лись на одном и том же рас­сто­я­нии от опуш­ки, по­это­му рас­сто­я­ние, ко­то­рое ещё оста­лось прой­ти до опуш­ки более мед­лен­но­му из них, равно рас­сто­я­нию, на ко­то­рое более быст­рый от неё уже уда­лил­ся. Сле­до­ва­тель­но, 4,4 − 2,5х = 3х − 4,4, от­ку­да х = 1,6 ч, а ис­ко­мое рас­сто­я­ние равно 2,5 · 1,8 = 4 км.

 

При­ве­дем дру­гое ре­ше­ние.

Тот, кто идет быст­рее, дой­дет до опуш­ки за 4,4 : 3 = 22/15 часа. За это время тот, кто идет мед­лен­нее, прой­дет 2,5 · 22/15 = 11/3 км и ока­жет­ся на рас­сто­я­нии 4,4 − 11/3 = 11/15 км от опуш­ки. Далее они пой­дут на встре­чу друг другу со ско­ро­стью сбли­же­ния 5,5 км/час и пре­одо­ле­ют раз­де­ля­ю­щее их рас­сто­я­ние за (11/15) : 5,5 = 2/15 часа. За это время мед­лен­но иду­щий пе­ше­ход прой­дет еще 2,5 · 2/15 = 1/3 км и ока­жет­ся на рас­сто­я­нии 11/3 + 1/3 = 4 км от точки от­прав­ле­ния.

Ответ: 4.

Ответ: 4

6. B 14 . Из го­ро­дов и , рас­сто­я­ние между ко­то­ры­ми равно 330 км, нав­стре­чу друг другу од­но­вре­мен­но вы­еха­ли два ав­то­мо­би­ля и встре­ти­лись через 3 часа на рас­сто­я­нии 180 км от го­ро­да . Най­ди­те ско­рость ав­то­мо­би­ля, вы­ехав­ше­го из го­ро­да . Ответ дайте в км/ч.

Ре­ше­ние.

Ав­то­мо­биль, вы­ехав­ший из го­ро­да , пре­одо­лел рас­сто­я­ние (330 – 180) км = 150 км за 3 часа. Пусть км/ч – ско­рость дан­но­го ав­то­мо­би­ля. Таким об­ра­зом,

 

км/ч.

Ответ: 50.

Ответ: 50

7. B 14 . Из одной точки кру­го­вой трас­сы, длина ко­то­рой равна 14 км, од­но­вре­мен­но в одном на­прав­ле­нии стар­то­ва­ли два ав­то­мо­би­ля. Ско­рость пер­во­го ав­то­мо­би­ля равна 80 км/ч, и через 40 минут после стар­та он опе­ре­жал вто­рой ав­то­мо­биль на один круг. Най­ди­те ско­рость вто­ро­го ав­то­мо­би­ля. Ответ дайте в км/ч.

Ре­ше­ние.

Пусть ско­рость вто­ро­го ав­то­мо­би­ля равна км/ч. За 2/3 часа пер­вый ав­то­мо­биль про­шел на 14 км боль­ше, чем вто­рой, от­сю­да имеем

 

.

Ответ: 59.

Ответ: 59

8. B 14 . Кли­ент А. сде­лал вклад в банке в раз­ме­ре 6200 руб­лей. Про­цен­ты по вкла­ду на­чис­ля­ют­ся раз в год и при­бав­ля­ют­ся к те­ку­щей сумме вкла­да. Ровно через год на тех же усло­ви­ях такой же вклад в том же банке сде­лал Б. Ещё ровно через год кли­ен­ты А. и Б. за­кры­ли вкла­ды и за­бра­ли все на­ко­пив­ши­е­ся день­ги. При этом кли­ент А. по­лу­чил на 682 рубля боль­ше кли­ен­та Б. Какой про­цент го­до­вых на­чис­лял банк по этим вкла­дам?

Ре­ше­ние.

Если в банк под про­цен­тов го­до­вых по­ло­же­на сумма , то через лет она ста­нет рав­ной По­это­му кли­ент А. за два года по­лу­чил руб., а кли­ент B. за год по­лу­чил По усло­вию, от­ку­да имеем:

 

 

Тем самым, банк на­чис­лял 10 про­цен­тов го­до­вых.

 

Ответ: 10.

Ответ: 10

9. B 14 .

Пер­вая труба на­пол­ня­ет ре­зер­ву­ар на 6 минут доль­ше, чем вто­рая. Обе трубы на­пол­ня­ют этот же ре­зер­ву­ар за 4 ми­ну­ты. За сколь­ко минут на­пол­ня­ет этот ре­зер­ву­ар одна вто­рая труба?

 

Ре­ше­ние.

Пусть вто­рая труба на­пол­ня­ет ре­зер­ву­ар за x минут, а пер­вая — за x + 6 минут. В одну ми­ну­ту они на­пол­ня­ют со­от­вет­ствен­но и часть ре­зер­ву­а­ра. По­сколь­ку за 4 ми­ну­ты обе трубы за­пол­ня­ют весь ре­зер­ву­ар, за одну ми­ну­ту они на­пол­ня­е­ют одну чет­вер­тую часть ре­зер­ву­а­ра:

 

.

 

Далее можно ре­шать по­лу­чен­ное урав­не­ние. Но можно за­ме­тить, что при по­ло­жи­тель­ных x функ­ция, на­хо­дя­ща­я­ся в левой части урав­не­ния, убы­ва­ет. По­это­му оче­вид­ное ре­ше­ние урав­не­ния — един­ствен­но. По­сколь­ку вто­рая труба за­пол­ня­ет ре­зер­ву­а­ра в ми­ну­ту, она за­пол­нит весь ре­зер­ву­ар за 6 минут.

Ответ: 6.

Ответ: 6

10. B 14 . В по­мощь са­до­во­му на­со­су, пе­ре­ка­чи­ва­ю­ще­му 5 лит­ров воды за 2 ми­ну­ты, под­клю­чи­ли вто­рой насос, пе­ре­ка­чи­ва­ю­щий тот же объем воды за 3 ми­ну­ты. Сколь­ко минут эти два на­со­са долж­ны ра­бо­тать сов­мест­но, чтобы пе­ре­ка­чать 25 лит­ров воды?