Задание В13

Вариант № 3712875

1. B 13 . Ра­ди­у­сы трех шаров равны 6, 8 и 10. Най­ди­те ра­ди­ус шара, объем ко­то­ро­го равен сумме их объ­е­мов.

Ре­ше­ние.

Объем та­ко­го шара

 

,

от­ку­да по­лу­чим, что .

Ответ: 12.

Ответ: 12

2. B 13 . 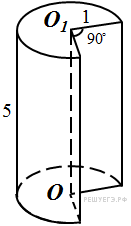Най­ди­те объем части ци­лин­дра, изоб­ра­жен­ной на ри­сун­ке. В от­ве­те ука­жи­те .

Ре­ше­ние.

Объем дан­ной части ци­лин­дра равен

 

.

Ответ: 3,75.

Ответ: 3,75

3. B 13 . Ра­ди­ус ос­но­ва­ния ко­ну­са равен 3, вы­со­та равна 4. Най­ди­те пло­щадь пол­ной по­верх­но­сти ко­ну­са, де­лен­ную на .

Ре­ше­ние.

Най­дем об­ра­зу­ю­щую по тео­ре­ме Пи­фа­го­ра: . Пло­щадь пол­ной по­верх­но­сти ко­ну­са

 

.

Ответ: 24.

Ответ: 24

4. B 13 . Объем шара равен 288 . Най­ди­те пло­щадь его по­верх­но­сти, де­лен­ную на .

Ре­ше­ние.

Объем шара ра­ди­у­са вы­чис­ля­ет­ся по фор­му­ле , от­ку­да

 

.

Пло­щадь его по­верх­но­сти:

.

Ответ: 144.

Ответ: 144

5. B 13 . Объем пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да равен 60. Пло­щадь одной его грани равна 12. Най­ди­те ребро па­рал­ле­ле­пи­пе­да, пер­пен­ди­ку­ляр­ное этой грани.

Ре­ше­ние.

Объем пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да равен , где — пло­щадь грани, а — вы­со­та пер­пен­ди­ку­ляр­но­го к ней ребра. Тогда

 

Ответ: 5.

Ответ: 5

6. B 13 . Ребра пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да, вы­хо­дя­щие из одной вер­ши­ны, равны 1, 2, 3. Най­ди­те его пло­щадь по­верх­но­сти.

Ре­ше­ние.

Пло­щадь по­верх­но­сти пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да равна удво­ен­ной сумме по­пар­ных про­из­ве­де­ний его из­ме­ре­ний

 

.

Ответ: 22.

Ответ: 22

7. B 13 . Ос­но­ва­ни­ем пря­мой тре­уголь­ной приз­мы слу­жит пря­мо­уголь­ный тре­уголь­ник с ка­те­та­ми 3 и 5. Объем приз­мы равен 30. Най­ди­те ее бо­ко­вое ребро.

Ре­ше­ние.

Объем пря­мой приз­мы равен где – пло­щадь ос­но­ва­ния, а – бо­ко­вое ребро. Тогда длина ее бо­ко­во­го ребра равна

 

.

Ответ: 4.

Ответ: 4

8. B 13 . Конус опи­сан около пра­виль­ной че­ты­рех­уголь­ной пи­ра­ми­ды со сто­ро­ной ос­но­ва­ния 4 и вы­со­той 6. Най­ди­те его объем, де­лен­ный на .

Ре­ше­ние.

Ра­ди­ус ос­но­ва­ния ко­ну­са равен по­ло­ви­не диа­го­на­ли квад­ра­та :   . Тогда объем ко­ну­са, де­лен­ный на :

 

Ответ: 16.

Ответ: 16

9. B 13 . Около куба с реб­ром  опи­сан шар. Най­ди­те объем этого шара, де­лен­ный на .

Ре­ше­ние.

Пусть длина ребра куба равна а, а его диа­го­наль равна d. Ра­ди­ус опи­сан­но­го шара R равен по­ло­ви­не диа­го­на­ли куба:

 

.

По­это­му объем шара равен

Тогда

Ответ: 4,5.

Ответ: 4,5

10. B 13

 .

Най­ди­те пло­щадь бо­ко­вой по­верх­но­сти пра­виль­ной тре­уголь­ной приз­мы, опи­сан­ной около ци­лин­дра, ра­ди­ус ос­но­ва­ния ко­то­ро­го равен , а вы­со­та равна 2.