30. Теорема об изменении кинетической энергии системы в абсолютном движении

 кинетическая энергия системы материальных точек в ее абсолютном движении равна сумме кинетической энергии поступательного (переносного) движения системы вместе с центром масс, и кинетической энергии движения системы относительно центра масс.

Теорема об изменении кинетической энергии системы в относительном движении

Работа кориолисовой силы инерции на любом относительном перемещении равна 0, и теорема об изменении кинетической энергии точки в относительном движении будет иметь вид(v1 и v0- значения относительных скоростей, А-работа на относительном перемещении): (mV1^2)/2-(mV0^2)/2=SAк+А(Fпер).

31, В чем заключается сущность принципа даламбера

Д’Аламбера принцип — в механике: один из основных принципов динамики, согласно которому, если к заданным (активным) силам, действующим на точки механической системы, и реакциям наложенных связей присоединить силы инерции, то получится уравновешенная система сил.

Принцип Д’Аламбера позволяет применить к решению задач динамики более простые методы статики, поэтому им широко пользуются в инженерной практике, т. н. метод кинетостатики. Особенно удобно им пользоваться для определения реакций связей в случаях, когда закон происходящего движения известен или найден из решения соответствующих уравнений.

32) Теорема об изменении количества движения материальной точки?

Для доказательства теоремы запишем дифференциальное уравнение движения точки (основное уравнение динамики точки) в виде mdV / dt = F. Напомним, что здесь F - равнодействующая сил, приложенных к точке. Внесем постоянную величину - m под знак производной и, разделяя переменные, получим математическую запись теоремы в дифференциальной форме: d(mV) = Fdt (1)

Произведение mV назовем количеством движения точки, произведение Fdt - элементарным импульсом силы (равнодействующей), что позволяет сформулировать теорему об изменении количества движения материальной точки в дифференциальной форме: дифференциал от количества движения материальной точки равен элементарному импульсу сил, приложенных к точке. Количество движения материальной точки - это векторная мера движения точки. Направление вектора количества движения точки q совпадает с направлением вектора скорости V. Единицей количества движения является кг·м/с.

Элементарный импульс силы - это векторная мера действия силы, отражающая, что действие силы зависит не только от величины и направления силы, но и от продолжительности действия силы.

Предположим, что за промежуток времени от V0 до V скорость точки изменилась от до , и при этих предположениях проинтегрируем (1). В результате получаем запись теоремы в интегральной форме:

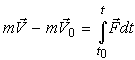(2)

Интеграл в правой части (2) назовем полным импульсом силы (равнодействующей) и сформулируем теорему об изменении количества движения материальной точки в интегральной форме: изменение количества движения материальной точки за некоторый промежуток времени равно полному импульсу сил, приложенных к точке. Заметим, что импульс силы измеряется в Н·м. Проектируя выражения (1) и (2) на оси координат, можно получить запись теоремы в дифференциальной и интегральной формах в координатном виде, что предлагается сделать самостоятельно. На практике теорема применяется, когда интеграл в правой части (2) можно взять, то есть когда

F = F(t) или F = const.

Чаще всего теорема применяется для решения задач, когда F = 0 и имеет место закон сохранения количества движения материальной точки. В этом случае определенный интеграл в правой части (2) равен нулю и

mV = const = mV0 (3)

то есть при равенстве нулю равнодействующей сил, приложенных к материальной точке, ее количество движения остается постоянным, равным своему начальному значению. Закон сохранения имеет место и при движении вдоль одной из осей, например Ox, когда Fx = 0. В этом случае mVx = const = mV0x.

33) теорема об изменение кинетической энергии механической системы?

ТЕОРЕМА. Изменение кинетической энергии механической системы на некотором перемещении равно сумме работ внешних и внутренних сил, действующих на систему, на том же перемещении.

Из теоремы следует закон сохранения механической энергии.

Если механическая система является консервативной, то полная механическая энергия системы Т + П, равная сумме кинетической и потенциальной энергий, при движении системы остается постоянной

При движении механической системы в потенциальном силовом поле получаем

T2 -T1 = A12.

По определению потенциальной энергии

П1 - П2 = A12.

Тогда

T2 - T1 = П1 - П2 , T2+ П2 = T1 + П1 , Т + П = const.

34) при каких условиях остается постоянным кинетический момент механической системы относительно оси?

Проектируя равенство, выражающее теорему об изменении кинетического момента, на ось , устанавливаем теорему об изменении кинетического момента механической системы относительно оси.

Теорема. Производная по времени от кинетического момента механической системы относительно неподвижной оси равна сумме моментов всех внешних сил, действующих на систему, относительно этой оси .

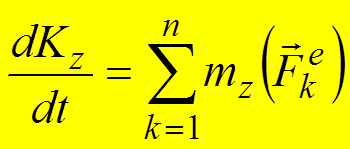
Следствие. Если сумма моментов внешних сил относительно какой-либо оси равна нулю, то кинетический момент системы относительно этой оси постоянен.

35) чему равна мощность сил, приложенных к твердому телу, вращающемуся вокруг неподвижной оси?

Предположим, что к твёрдому телу, вращающемуся вокруг неподвижной оси Z, приложены внешние силы . Вычислим сначала элементарную работу отдельной силы , которая приложена в точке , описывающей окружность радиусом . Разложим эту силу на три составляющие, направленные по естественным осям траектории точки . Определим момент силы относительно оси z как сумму моментов её составляющих относительно этой оси. В общем момент силы относительно оси Z равен моменту силы , которая лежит в плоскости, перпендикулярной оси Z . При элементарном перемещении тела его угол поворота φ получает приращение dφ, а дуговая координата точки - приращение . Вычислим работу силы на этом перемещении как сумму работ трёх её составляющих. Работа сил перпендикулярных вектору скорости точки , равна 0, поэтому элементарная работа силы . Элементарная работа всех сил, приложенных к твёрдому телу , где - Главный момент внешних сил относительно оси вращения z. Таким образом , т.е. элементарная работа сил, приложенных к твёрдому телу, вращающемуся вокруг неподвижной оси, равна произведению главного момента внешних сил относительно оси вращения на приращение угла поворота. Мощность вычисляется по следующей формуле:

36) как определить работу переменной силы?

В случае переменной силы, разбиваем весь путь S на столь малые отрезки dS,где силы, действующие на каждом из них, можно считать постоянными.

F

dS_ί

_ί

F_ί

S

Работу определяем по формуле dA_ί =F_ί d S_ί cos_ί

Тогда работа на всем пути определяется как сумма всех работ на малых участках, _n

A= Σd A_ί

ⁱ⁼¹

Или в предельном случае дробления на бесконечно малые участки.

Здесь все величины или их часть непостоянны. Чтобы найти этот интеграл, надо знать зависимость F,от S и .

37) чему равна работа сил тяжести и упругости?

Работа силы упругости

Когда вы растягиваете или сжимаете пружину, то есть дефор­мируете ее, приложенная вами сила совершает положительную работу, так как направление силы совпадает с направлением пе­ремещения. Действующая же со стороны пружины сила упругости совершает при этом отрицательную работу, потому что эта сила направлена противоположно перемещению. Зато при распрямлении пружины, то есть возвращении ее в недеформированное состояние, сила упругости совершает положи­тельную работу, так как направление силы упругости совпадает при этом с направлением перемещения. Эта работа равна той ра­боте, которую мы совершили, деформируя пружину.

Работа силы тяжести

При подъеме тела массой m на высоту h сила тяжести совершает отрицательную работу А = - mgh, так как при этом сила тяжести направлена противоположно перемещению. Зато при движении тела вниз совершает положительную работу А = mgh, так как направление силы тяжести совпадает с направлением перемещения.

Если тело движется по произвольной траектории, его движение можно представить как «ступенчатое», то есть состоящее из небольших горизонтальных и вертикальных участков.

Суммарная работа силы тяжести на всех горизонтальных участках равна нулю, а алгебраическая (с учетом знака) сумма работ на всех вертикальных участках равна mg(h1 - h2), где h1 — начальная высота, h2 — конечная высота. Таким образом, при движении по любой траектории работа силы тяжести А = mg(h1 – h2). Мы видим, что эта работа зависит только от положения начальной и конечной точек траектории и не зависит от ее формы. В частности, если тело вернулось в начальную точку, работа силы тяжести равна нулю.

38. Кинетической энергией системы называется скалярная величина Т, равная арифметиче­ской сумме кинетических энергий всех точек системы

39. Дифференциальные уравнения движения материальной точки: , в проекции на декартовы оси коорд.: , на оси естественного трехгранника: ; ; ( – проекция ускорения на бинормаль), т.е. (– радиус кривизны траектории в текущей точке). В случае плоского движения точки в полярных координатах: .

Две основные задачи динамики:

При решении этих задач исходными являются дифференциальные уравнения движения точки, записанные в общем виде в декартовых или естественных координатах.

40. Работа силы трения: если сила трения const, то - всегда отрицательна, , f – коэфф.трения, N – нормальная реакция поверхности.

41.Формы дифференциальных уравнений движения

1) 2-ой закон Ньютона – для количества движения.

2) Умножим на   (векторно):

или   - уравнение момента количества движения.

[Почему? – самостоятельно. Учесть   ].

Производная по времени от момента количества движения геометрически равна моменту силы.

Подробная запись (координатная):

3) Умножим скалярно на элементарные перемещения   :

 .

 - уравнение кинетической энергии.  

Дифференциал кинетической энергии точки равен элементарной работе суммы сил, приложенных к точке, на действительном перемещении.

О первых интегралах (законы сохранения).

Из дифференциальных уравнений: функция координат, их производных по времени, являющаяся постоянной в силу уравнений (то есть её производная по времени равна нулю) => называется первым интегралом.