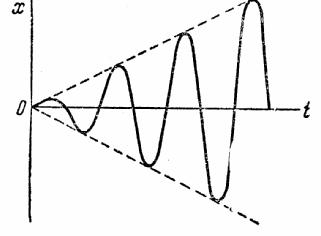
11Условия резонанса.

Резонанс. В случае, когда  , т.е. когда частота возму­щающей силы равна частоте собственных колебаний, имеет место так называемое явление резонанса. Размахи вынужденных колебаний при резонансе будут со временем неограниченно возрастать так, как показано на рис.35.

12 свободная и не свободная материальная точка. Дифференциальное уравнение движения. Для свободной материальной точки задачами дина­мики являются следующие: 1) зная закон движения точки, определить действующую на нее силу (первая задача динамики); 2) зная дей­ствующие на точку силы, определить закон движения точки (вторая или основная задача динамики).

Решаются обе эти задачи с помощью уравнений, вы­ражающих основной закон динамики, так как эти уравнения связывают ускорение   т.е. величину, характеризующую движение точки, и действующие на нее силы.

В технике часто приходится сталкиваться с изучением несвобод­ного движения точки, т.е. со случаями, когда точка, благодаря на­ложенным на нее связям, вынуждена двигаться по заданной неподвиж­ной поверхности или кривой.

Несвободной материальной точкой называется точка, свобода движения которой ограничена.

Тела, ограничивающие свободу движения точки, называются связями.

Пусть связь представляет собой поверхность какого-либо тела, по которой движется точка.  Тогда координаты точки должны удовлетворять уравнению этой поверхности,  которое называется уравнением связи.

Если точка вынуждена двигаться по некоторой линии, то уравнениями связи являются уравнения этой лини.

,             

Таким образом, движение несвободной материальной точки зависит не только от приложенных к ней активных сил и начальных условий, но так же от имеющихся связей. При этом значения начальных параметров должны удовлетворять уравнениям связей.

Связи бывают двухсторонние или удерживающие и односторонние или неудерживающие.

Связь называется двухсторонней если, накладываемые ею на координаты точки ограничения выражаются в форме равенств, определяющих кривые или поверхности в пространстве на которых должна находится точка.

С помощью дифференциальных уравнений движения решается вторая задача динамики. Правила составления таких уравнений зависят от того, каким способом хотим определить движение точки.

 

1) Определение движения точки координатным способом.

Рассмотрим свободную материальную точку, движущуюся под действием сил  , ,..,  . Проведем неподвижные координатные оси Oxyz (рис.4). Про­ектируя обе части равенства   на эти оси и учитывая, что   и т.д., получим дифферен­циальные уравнения криволинейного дви­жения точки в проекциях на оси прямо­угольной декартовой системы координат:

,   ,  .

Рис.4

   

Так как действующие на точку силы мо­гут зависеть от времени, от положения точки и от ее скорости, то правые части уравнений могут содержать время t, координаты точки х, у, z и проекции ее скорости  . При этом в правую часть каждого из уравнений могут входить все эти переменные.

Чтобы с помощью этих уравнений решить основную задачу динамики, надо, кроме действующих сил, знать еще начальные условия, т.е. положение и скорость точки в начальный момент. В координатных осях Oxyz начальные условия задаются в виде: при 

. 

Зная действующие силы, после интегрирования уравнений найдем координаты х, y, z движущейся точки, как функции времени t, т.е. найдем закон движения точки.