Модифицированный метод Ньютона сходится медленнее, чем исходный (немодифицированный) метод, однако менее сложен при вычислениях и потому часто оказывается предпочтительным.
2 Численное интегрирование
В ряде задач возникает необходимость вычисления определенного интеграла от некоторой функции:
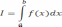
Для некоторых функций значение интеграла можно найти точно. Однако в общем случае значение интеграла можно найти только приближенно, используя тот или иной способ численного интегрирования.
Способы численного вычисления определенных интегралов основаны на замене интеграла конечной суммой [4]:
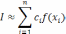
где
–
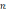число
точек, в которых вычисляется значение
подынтегральной функции;
точки
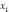– узлы метода;
числа
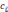– числовые коэффициенты квадратурной
формулы.
Часто формулы для оценки значения интеграла называют квадратурными формулами. Погрешность квадратурной формулы зависит как от выбора коэффициентов , так и от расположения узлов
При замене подынтегральной функции на полином нулевой, первой и второй степени получаются соответственно методы прямоугольников, трапеций и парабол.
2.1 Метод Симпсона
Метод Симпсона (метод парабол) позволяет получить значение определенного интеграла с требуемой степенью точности.
Пусть
функция y =
f(x) непрерывна
на отрезке [a;
b] и нам
требуется вычислить определенный
интеграл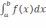 
.
Разобьем
отрезок [a;
b] на n
элементарных отрезков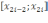 
,
длины 
точками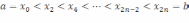 
.
Пусть точки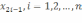 
являются серединами отрезков 
cоответственно.
В этом случае все "узлы" определяются
из равенства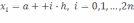 
.
На
каждом интервале
,
подынтегральная функция приближается
квадратичной параболой 
, проходящей через точки 
. Отсюда и название метода - метод парабол.
Это
делается для того, чтобы в качестве
приближенного значения определенного
интеграла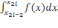 
взять 
,
который мы можем вычислить по формуле
Ньютона-Лейбница. В этом заключается
суть
метода парабол.
Геометрически метод парабол представлен на рисунке 2.1.1.
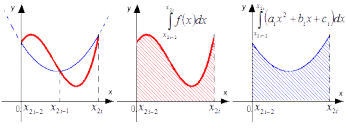
Рисунок 2.1.1 – Геометрический метод парабол
Графическая иллюстрация метода Симпсона представлена на рисунке 2.1.2. Красной линией изображен график функции y=f(x), синей линией показано приближение графика функции y=f(x) квадратичными параболами на каждом элементарном отрезке разбиения.
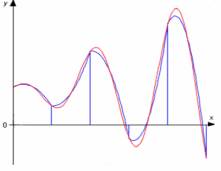
Рисунок 2.1.2 – Графическая иллюстрация метода парабол (Симпсона)
Выведем формулу метода Симпсона (парабол). В силу пятого свойства определенного интеграла имеем
.
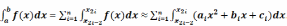
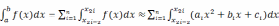Для получения формулы метода парабол (Симпсона) вычислим
.
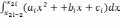Пусть
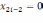(мы всегда можем к этому прийти, проведя
соответствующее геометрическое
преобразования сдвига для любого i
= 1, 2, ..., n).
Сделаем чертеж (рисунок 2.1.3).
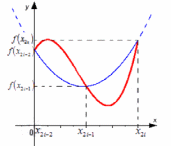
Рисунок 2.1.3
Покажем,
что через точки 
проходит только одна квадратичная
парабола
.
Другими словами, докажем, что коэффициенты
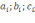определяются единственным образом.
Так как - точки параболы, то справедливо каждое из уравнений системы
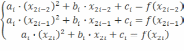
Записанная
система уравнений есть система линейных
алгебраических уравнений относительно
неизвестных переменныx
.
Определителем основной матрицы этой
системы уравнений является определитель
Вандермонда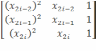 
,
а он отличен от нуля для несовпадающих
точек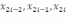 
.
Это указывает на то, что система уравнений
имеет единственное решение, то есть,
коэффициенты
определяются единственным образом, и
через точки
проходит единственная квадратичная
парабола.
Перейдем
к нахождению интеграла 
.
Очевидно:
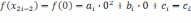
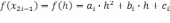
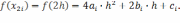
Используем эти равенства, чтобы осуществить последний переход в следующей цепочке равенств:
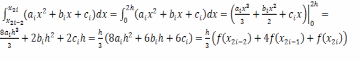
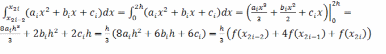
Таким образом, можно получить формулу метода парабол:
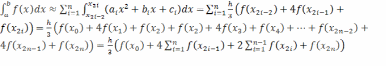
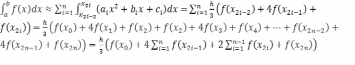Формула
метода Симпсона (парабол)
имеет вид
Схема алгоритма метода Симпсона приведена на рисунке 2.1.4
Рисунок 2.1.4 – Схема метода Симпсона
2.2 Реализация метода Симпсона
Для
вычисления определенного интеграла
,
где 
,
с заданной точностью 
воспользуемся средствами MathCad.
В
панель вычисления (“Calculus
Toolbar”)
есть специальный инструмент
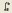– «определенный интеграл» для численного
и символьного нахождения результата.
Данные вносятся в соответствии с
принятыми правилами записи определенного
интеграла – над знаком и под знаком
указываем границы интегрирования,
справа от знака - функцию интегрирования
[6].
Введем функцию и заданную точность
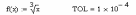
Введем заданный интервал
Вычислим интеграл
Решим интеграл методом Симпсона.
Разобьем интервал на отрезки,
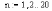
В формуле должно быть четное количество отрезков, поэтому применим 2*n
Ответ:
х=11.2499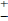 
0.0001
Графически значение интеграла представляет собой площадь, заключенную в заданном интервале под заданной функцией.
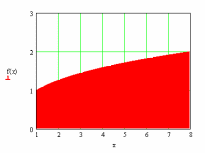
Рисунок 2.2.1
Код программы, производящей численное интегрирование методом Симпсона, на языке программирования C# представлен ниже:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace Метод_Симпсона
{/*Данная программа вычисляет значение определенного интеграла методом Симпсона */
/*на отрезке [1;8] с точностью e=10^(-3)*/
class Program
{
static double Ff( double x) // Задаем функцию
{/*В функции меняем кубический корень на степень 1/3 */
double k = 1, m = 3, z = k / m;
double y = Math.Pow(x, z);
return y;
}
static void Main() // Вход в программу
{
double a = 1, b = 8;
Console.WriteLine("Нижний предел- {0}",a);
Console.WriteLine("Верхний предел- {0}",b);
int n = 14;
Console.WriteLine("Количество отрезков- {0}",n);
double h = (b - a)/(n); // Определяем шаг узлов разбиения
Console.WriteLine("Шаг- {0}\n",h);
int i = 1; // первый узел разбиения
/*Инициализируем первую и последнюю функции f(x),*/
/*а также суммы четных и нечетных функций f(x)*/
double Summa = 0, Summa1 = 0, Summa2 = 0, SummaE1 = 0, SummaE2 = 0;
double k = 1, m = 3, z = k/m;
for (double x; i < n; i++)
{
x = a + i * h; // Номер нечетного узла
Console.WriteLine("X (нечет) = {0}", x);
Summa1 = 4 * Ff(x);//Формула для определения нечетных f(x)
SummaE1 += Summa1; // Сумма нечетных функций f(x)
Console.WriteLine("SummaE1 равна {0:f4}\n", SummaE1);
i++; if (i == 14)break;
Console.WriteLine("Следущий узел {0:f4}\n", i);
x = a + i * h; // Номер четного узла
Console.WriteLine("X (чет) = {0}", x);
Summa2 = 2 * Ff(x); //Формула для определения четных f(x)
SummaE2 += Summa2; // Сумма четных функций f(x)
Console.WriteLine("СуммаE2 равна {0:f4}\n", SummaE2);
}
Console.WriteLine("Итого SummaE1 равна {0:f4}", SummaE1);
Console.WriteLine("Итого SummaE2 равна {0:f4}", SummaE2);
/*Вызываем функцию для определения первой и последней функции f(x)*/
Console.WriteLine("Ff(a) равен {0:f4}", Ff(a));
Console.WriteLine("Ff(b) равен {0:f4}\n", Ff(b));
/*Вводим формулу для определения значения определенного инеграла*/
Summa = (h/3)*(SummaE1 + SummaE2 + Ff(b) +Ff(a));
Console.WriteLine("Интеграл равен {0:f4}\a", Summa);
return;
}
}
}
Результат выполнения и работы программы изображен на рисунке 2.2.2.
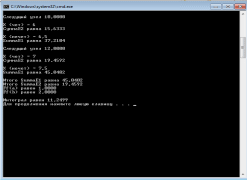
Рисунок 2.2.2 – Выполнение программы
Вышеизложенная программа разбита на функциональные блоки – методы, отвечающие за свои операции:
static void Main() выводит на экран интегрируемую функцию, границы интегрирования, а также точность вычислений, вызывает метод, осуществляющий расчет.
по завершению каждого метода выводит на экран результаты расчетов.
double Func(double x) возвращает вызвавшему его методу значение исходной функции в точке x.
Также были применены стандартные методы библиотек C# [7]:
Console.WriteLine(string format, params object[] arg) выводит в консоль текстовые представления заданного массива объектов, за которым следует текущий признак конца строки;
Math.Pow(double x, double y) возвращает указанное число x, возведенное в указанную степень y;
for структура повторения автоматически контролирует все детали повторения.
Метод Симпсона обеспечивает большую точность вычисления по сравнению с методом прямоугольников и трапеций.