Министерство образования и науки Российской Федерации

Филиал федерального государственного бюджетного образовательного учреждения

высшего профессионального образования

«Южно-Уральский государственный университет»

(НУИ) в г. Златоусте

Факультет «Машиностроительный»

Кафедра «Математики и вычислительной техники»

КУРСОВОЙ ПРОЕКТ

по дисциплине «Прикладное программирование»

Вариант 6

Выполнил:

студент группы ФТТ-333

_________/Гаффаров А.С/

«__01__»___05___2014 г.

Проверил:

преподаватель

_________/Соколова Е.В./

«___»__________2014_г.

Работа выполнена с

оценкой _______________

Златоуст

2014

Оглавление

Введение 4

Рассмотрим модифицированный метод Ньютона (метод секущих). 7

Модифицированный метод Ньютона сходится медленнее, чем исходный (немодифицированный) метод, однако менее сложен при вычислениях и потому часто оказывается предпочтительным. 14

2 ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ 15

Рисунок 2.1.1 – Геометрический метод парабол 17

Графическая иллюстрация метода Симпсона представлена на рисунке 2.1.2. Красной линией изображен график функции y=f(x), синей линией показано приближение графика функции y=f(x) квадратичными параболами на каждом элементарном отрезке разбиения. 17

Рисунок 2.1.2 – Графическая иллюстрация метода парабол (Симпсона) 17

Выведем формулу метода Симпсона (парабол). В силу пятого свойства определенного интеграла имеем 18

. 18

Для получения формулы метода парабол (Симпсона) вычислим 18

3 ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ 27

Суть метода наименьших квадратов заключается в нахождении коэффициентов линейной зависимости, при которых функция двух переменных а и b принимает наименьшее значение. То есть, при данных а и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. 28

Введение 3

1 Численное решение нелинейных уравнений 4

1.1 Модифицированный метод Ньютона 6

1.2 Решение уравнения модифицированным методом Ньютона 8

2 Численное интегрирование 14

2.1 Метод Симпсона 14

2.2 Реализация метода Симпсона 19

3 Обработка экспериментальных данных 25

3.1 Метод наименьших квадратов 25

3.2 Реализация метода наименьших квадратов 27

Заключение 33

‎библиографический список 34

Введение

В 1970-х - 80-х годах XX века с появлением персональных компьютеров начинает развиваться прикладное программное обеспечение.

В связи с развитием новой вычислительной техники инженерная практика наших дней все чаще встречается с математическими задачами, точное решение которых получить весьма сложно или невозможно. В этих случаях обычно прибегают к тем или иным приближенным вычислениям. Вот почему приближенные и численные методы математического анализа получили за последние годы широкое развитие и приобрели исключительно важное значение.

Предметом изучения прикладного программирования являются численные методы решения задач математического анализа: изучение алгоритма метода, условия сходимости итерационных методов, изучение границ применимости методов, исследования оценок погрешностей методов и вычислений.

Программирование принято разделять на системное и прикладное. Системные программисты занимаются разработкой системного программного обеспечения: операционных систем, утилит и пр., а также систем программирования. Прикладные программисты создают прикладные программы: редакторы, табличные процессоры, игры, обучающие программы и многие другие. Прикладное ПО работает только при наличии системного ПО. Разработка любой программы начинается с построения алгоритма решения задачи.

В ходе данной работы необходимо освоить стандартные алгоритмы решения задач, научиться использовать возможности математического редактора MathCad для решения поставленных задач, изучить основные конструкции языка программирования C#.

Полученные знания необходимо использовать для решения задач вычислительной математики, т.е. реализовать алгоритмы средствами языка программирования C# и применить встроенные средства MathCad для проверки полученных результатов.

1 Численное решение нелинейных уравнений

Если законы функционирования модели нелинейны, а моделируемые процесс или система обладают одной степенью свободы (т.е. имеют одну независимую переменную), то такая модель, как правило, описывается одним нелинейным уравнением.

Необходимость отыскания корней нелинейных уравнений встречается в расчетах систем автоматического управления и регулирования, собственных колебаний машин и конструкций, в задачах кинематического анализа и синтеза, плоских и пространственных механизмов и других задачах.

Дано нелинейное уравнение: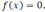

Необходимо решить это уравнение, т. е. найти его корень .

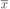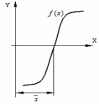
Рис. 1.1

Если функция имеет вид многочлена степени m,

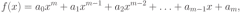
где a_i - коэффициенты многочлена, , то уравнение f(x)=0 имеет m корней (рисунок 1.2).

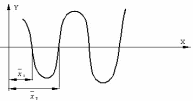
Рис. 1.2

Если функция f(x) включает в себя тригонометрические или экспоненциальные функции от некоторого аргумента x, то уравнение называется трансцендентным уравнением. Такие уравнения обычно имеют бесконечное множество решений.

Как известно, не всякое уравнение может быть решено точно. В первую очередь это относится к большинству трансцендентных уравнений.

Доказано также, что нельзя построить формулу, по которой можно было бы решать произвольные алгебраические уравнения степени, выше четвертой.

Однако точное решение уравнения не всегда является необходимым. Задачу отыскания корней уравнения можно считать практически решенной, если мы сумеем найти корни уравнения с заданной степенью точности. Для этого используются приближенные (численные) методы решения.

Большинство употребляющихся приближенных методов решения уравнений являются, по существу, способами уточнения корней. Для их применения необходимо знание интервала изоляции [a,b], в котором лежит уточняемый корень уравнения (рисунок 1.3).

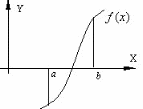
Рис. 1.3

Процесс определения интервала изоляции [a,b], содержащего только один из корней уравнения, называется отделением этого корня.

Процесс отделения корней проводят исходя из физического смысла прикладной задачи, графически, с помощью таблиц значений функции f(x) или при помощи специальной программы отделения корней. Процедура отделения корней основана на известном свойстве непрерывных функций: если функция непрерывна на замкнутом интервале [a,b] и на его концах имеет различные знаки, т.е. f(a)f(b)<0, то между точками a и b имеется хотя бы один корень уравнения. Если при этом знак функции f'(x) на отрезке [a,b] не меняется, то корень является единственным на этом отрезке.

Процесс определения корней алгебраических и трансцендентных уравнений состоит из 2 этапов:

1. отделение корней, - т.е. определение интервалов изоляции [a,b], внутри которого лежит каждый корень уравнения;

2. уточнение корней, - т.е. сужение интервала [a,b] до величины равной заданной степени точности .

Для алгебраических и трансцендентных уравнений пригодны одни и те же методы уточнения приближенных значений действительных корней:

1. метод половинного деления (метод дихотомии);

2. метод простых итераций;

3. метод Ньютона (метод касательных);

4. модифицированный метод Ньютона (метод секущих);

5. метод хорд и др.

1.1 Модифицированный метод Ньютона