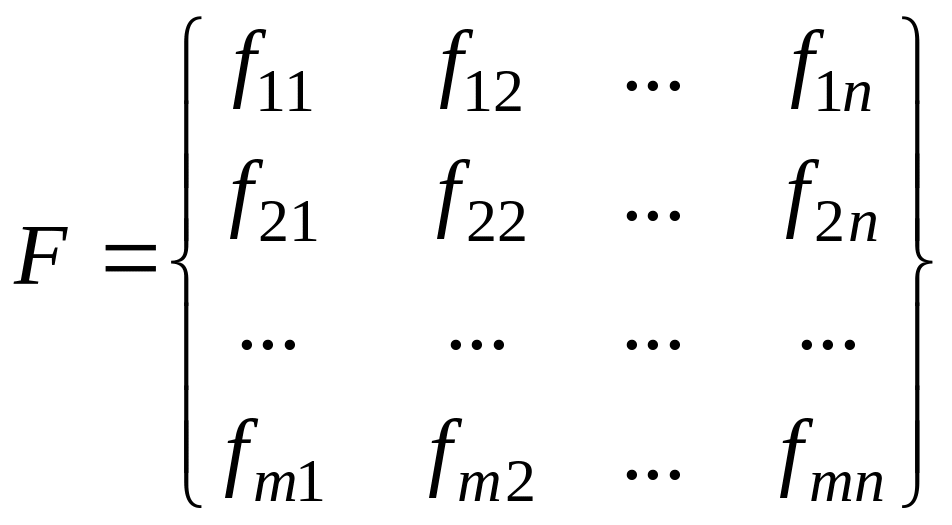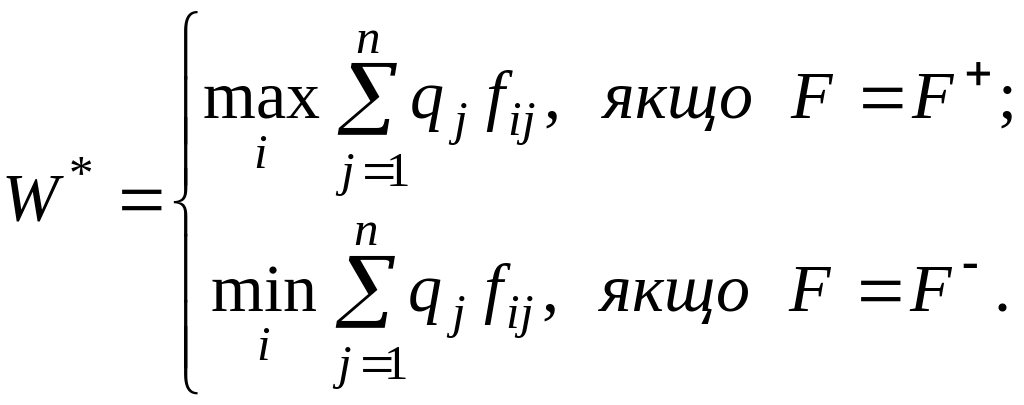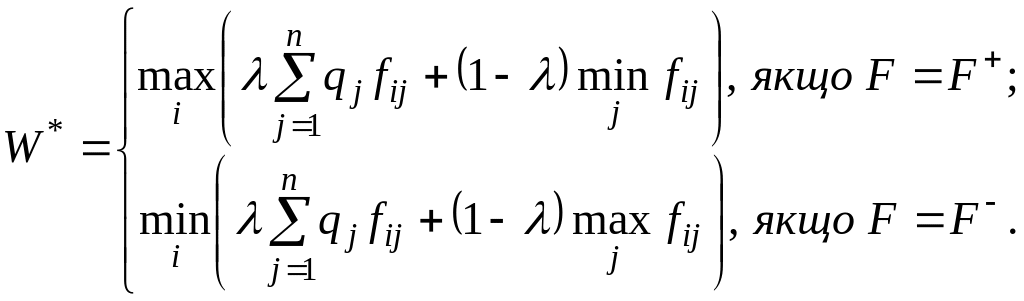Тема 2.2 Ухвалення рішення в умовах невизначеності на базі концепції теорії гри

Для прийняття оптимальних рішень і умовах невизначеності використовують математичні моделі, які дозволяють певним чином формалізувати процес прийняття рішення. Однією з таких моделей є теорія ігор.

Необхідно вказати, що теорія ігор – це розділ сучасної математики, який вивчає математичні моделі прийняття рішень в умовах невизначеності, конфліктності, тобто в ситуаціях, коли інтереси сторін або протилежні або не збігаються.

Гра – це формалізований опис (модель) конфліктної ситуації, яка включає в себе чітко визначені правила дій її учасників, котрі намагаються перемогти обираючи конкретну стратегію поведінки. При цьому жоден з гравців не знає яку стратегію обере інший але може кількісно оцінити ефективність результату реалізації обраної стратегії.

Складовими гри є:

1. Перший гравець (або особа, що приймає рішення (ОПР)), який може прийняти рішення з множини

,

2.27

яку називають множиною чистих стратегій. Одна з цих стратегій обов’язково має бути обрана.

2. Другий гравець – в економіці, наприклад, – це економічне середовище, яке знаходиться в одному попарно з несумісних станів з множини

2.28

одна з яких обов’язково настане.

3. Функціонал оцінювання – матриця кількісних оцінок ефективності результату реалізації множини стратегій ОПР (першого гравця) за умови реалізації стратегій другого гравця, наприклад, певний стан економічного середовища

2.29

де - кількісна оцінка діяльності першого гравця у випадку, коли він обрав стратегію , а другий гравець – стратегію .

Етапи гри:

• формулювання переліку стратегій першого та другого гравця – множин та ;

• визначення та формалізація основних показників ефективності стратегії ОПР – побудова матриці ;

• визначення (ідентифікація) інформаційної ситуації (ІС), яка характеризує поведінку другого гравця (економічного середовища);

• вибір критерію прийняття рішення з множини можливих критеріїв в залежності від ідентифікованої ІС;

• прийняття, згідно з вибраним критерієм, рішення із сукупності чистих або змішаних стратегій, якщо використання останніх можливе.

Необхідно також дати поняття інформаційної ситуації.

Під інформаційною ситуацією розуміють певний ступінь градації невизначеності щодо стратегії другого гравця (стану економічного середовища) у момент прийняття рішення ОПР.

Виділяють наступні інформаційні ситуації:

І₁ – характеризується заданим апріорним розподілом імовірностей станів економічного середовища:

2.30

І₂ – характеризується заданим розподілом апріорних імовірностей станів економічного середовища з точністю до певних невідомих параметрів.

І₃ – характеризується сукупністю обмежень щодо імовірностей станів економічного середовища.

І₄ – характеризується невідомим розподілом станів економічного середовища з одночасною відсутністю з його боку активної протидії ОПР.

І₅ – характеризується абсолютно протилежними інтересами ОПР та економічного середовища, тобто економічне середовище є антагоністом ОПР.

І₆ – є проміжною між І₁ і І₅, тобто, одночасно із заданим апріорним розподілом імовірностей станів економічного середовища, воно є антагоністом для ОПР.

І₇ – характеризується нечіткою множиною станів економічного середовища.

Необхідно також наголосити на тому, що формальна складова прийняття рішення в умовах невизначеності включає в себе знання множини критеріїв, на основі яких і здійснюється прийняття рішення, а також вміння обирати один з наявних критеріїв у відповідності до наявної інформаційної ситуації.

Критерії Байєса і Лапласа. Якщо ОПР перебуває в першій інформаційній ступці (І₁), то вважається заданим розподіл станів економічної системи (ЕС).

; ; .

2.31

Критерієм прийняття рішення в даному випадку є критерій Байєса: оптимальною вважається така стратегія , для якої , де:

- ціна гри ОПР при виборі оптимальної стратегії (в розумінні того чи іншого критерію), а - ціні гри ОПР при виборі стратегії .

2.32

У формі функціонал оцінювання розглядається для оптимізації виграшу, а у формі у випадку оптимізації втрат, збитків тощо.

Якщо всі стани ЕС рівноімовірні, тобто , то критерій Байєса перетворюється в критерій Лапласа: оптимальною вважають таку стратегію , для якої , де:

2.33

Для інформаційних ситуацій І₂ – І₄ критерії прийняття рішення будуть подібними, але дещо відрізнятимуться від них, оскільки розподіл станів ЕС не є точно визначеним.

Критерії Вальда та Севіджа. Якщо ОПР перебуває в п’ятій інформаційній ситуації (І₅), вважається, що ЕС є супротивником ОПР. Найчастіше в такій ситуації застосовують критерій Вальда: оптимальною вважають таку стратегію , для якої , де:

2.34

Даний критерій є безризиковим, оскільки враховує найгіршу ситуацію.

Критерій Вальда інколи подають дещо в іншій формі. Спочатку за платіжною матрицею утворюють іншу матрицю такої ж розмірності за наступним правилом:

2.35

Далі для визначення оптимальної стратегії до матриці застосовують критерій Вальда. Оскільки незалежно від інгредієнта платіжної матриці , , то формулювання отриманого критерію, який носить назву критерій Севіджа буде наступним: оптимальною вважають таку стратегію , для якої , де:

2.36

Критерій Гурвіца та Хеджеса-Лемана застосовується в інформаційній ситуації І₆ або І₇, або ж у ситуації, яку неможливо класифікувати. Нехай - деякий наперед заданий параметр. Тоді за критерієм Гурвіца оптимальною вважають таку стратегію , для якої , де:

2.37

В даному критерії враховано як найпесимістичніший, так і найоптимістичніший прогнози. Зокрема при отримуємо критерій Вальда (песимістичний прогноз), а при - критерій найкращого результату (оптимістичний прогноз).

Нехай тепер - деякий наперед заданий параметр, тоді за критерієм Ходжеса-Лемана оптимальною вважають таку стратегію , для якої , де:

2.38