2. Дифференциальные уравнения движения материальной точки. Задачи динамики точки 1-24

Векторное ДУ движения материальной точки :

ДУ в декартовой системе координат

скалярное ДУ

ДУ в естественной форме

На основе дифференциальных уравнений движения мате

риальной точки решают две задачи динамики точки:1) по

движению определить силы, производящие данное движение.

Эту задачу называют прямой задачей динамики. 2) – даны силы,

действующие на данный материальный объект; требутся опреде

лить движение этого объекта под действием данных сил. Эту задачу

называют второй задачей динамики.

3. Механическая система. Внешние и внутренние силы 1-6

Механическая система – это система материальных точек,

каждая из которых имеет определенную массу и занимает в данный

момент времени определенное положение в пространстве. Рассмотрим

систему, состоящую из п материальных точек. Распределение масс в

системе можно определить

значениями масс 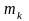ее точек и их координатами .

Действующие на механическую систему активные силы и реакции связей разделяют на внешние и внутренние. Внешними называют силы, действующие на точки системы со стороны точек или тел, не входящих в состав данной системы. Внутренними называют силы, с которыми точки или тела данной системы действуют друг на друга. Это разделение является условным и зависит от того, какая механическая система рассматривается. Например, если рассматривается движение всей Солнечной системы, то сила притяжения Земли к Солнцу будет внутренней; если же рассматривается движение системы Земля — Луна, то для этой системы та же сила будет внешней.

Внутренние силы обладают следующими свойствами:

1. Геометрическая сумма (главный вектор) всех внутренних сил системы равняется нулю.

2. Сумма моментов (главный момент) всех внутренних сил системы относительно любого центра или оси равняется нулю.

4. Масса системы. Центр масс 1-6

Масса системы М равна арифметической сумме масс всех точек или

тел, образующих систему. Если система представляет собой твердое тело,

то его масса является мерой инертности тела при поступательном

движении.

Центром масс механической системы называют геометрическую

точку С, радиус вектор которой определяется как

5. Теорема о движении центра масс механической системы. Дифференциальные уравнения поступательного движения тела 2-25

Дифференциальные уравнения движения системы материальных

точек в векторной форме имеют вид:

или

,

где скорость k – ой точки.

Теорема о движении центра масс механической системы формули

руется так: центр масс механической системы движется как

материальная точка, как бы обладающая массой системы, под

действием всех внешних сил, действующих на точки системы.

6. Количество движения материальной точки и механической системы 2-21

Количеством движения материальной точки называется

векторная величина, равная произведению массы точки на

вектор ее скорости

.

Количеством движения механической системы называется

векторQ, равный геометрической сумме количеств движения

всех точек системы:

Вектор Q является свободным вектором. Единица измерения

в системе СИ – кг ∙м/с. Используя понятие центра масс механи

ческой системы, количество движения системы будет

.