6. Скорости и ускорения точек вращающегося тела 1-9

Скорость точки будет равна

или .

Эту скорость называют линейной или окружной скоростью точки.

Она всегда направлена по касательной к окружности, описываемой

точкой М. Так как для всех точек тела ω одинакова, то скорости

точек пропорциональны расстояниям от оси вращения.

Для определения ускорения точки воспользуемся формулами

.

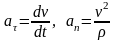Используя формулу (7) и учитывая, что ρ=h , найдем

Касательное ускорение направлено всегда по касательной к

траектории (окружности); нормальное ускорение – по радиусу к

оси вращения (рис. 3).

Полное ускорение точки

7. Плоско-параллельное движение твердого тела. Разложение движения на поступательное и вращательное 2-13

Плоским движением твердого тела называется такое

движение, при котором все его точки движутся в плоскостях,

параллельных данной неподвижной плоскости n.

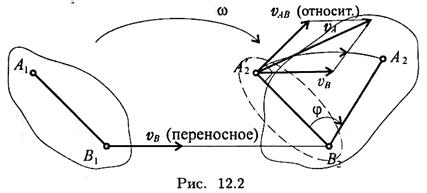
Разложение используют для определения скорости любой точки тела, применяя теорему о сложении скоростей (рис. 12.2).

Точка А движется вместе с точкой В, а затем поворачивается вокруг В с угловой скоростью и, тогда абсолютная скорость точки А будет равна

v_A = v_B + v_AB, v_AB = ωr (r = АВ).

П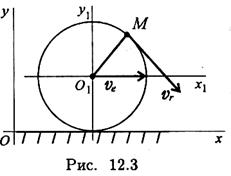 римером плоскопараллельного движения может быть движе­ние колеса на прямолинейном участке дороги (рис. 12.3).

Скорость точки М

v_M=v_e + v_r,

v_e — скорость центра колеса переносная; v_r — скорость вокруг центра относитель­ная.

уОх — неподвижная система координат,

y₁0₁x₁ — подвижная система координат, связанная с осью колеса.

8. Теорема об определении скоростей точек плоской фигуры 2-12

Скорость любой точки плоской фигуры равна геометрической сумме скорости выбранного полюса и скорости точки во вращательном движении фигуры вокруг полюса. 

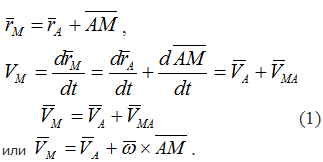
Производная от вектора AM, постоянного по величине и переменного по направлению, численно равна скорости  точки  М     при    вращении   ее вокруг точки А.

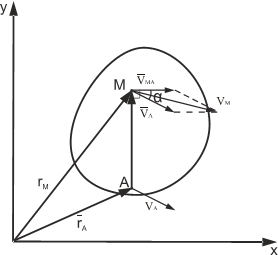
Рис. 1.3

Вектор V_MA= ω⋅AM перпендикулярен отрезку АМ.

Численную величину скорости точки М можно получить, если воспользоваться теоремой косинусов

или спроецировать векторное равенство (1) на выбранные оси координат

9. Мгновенный центр скоростей. Свойства и методы его определения 1-7

Мгновенным центром скоростей называется точка плоской фигу­ры, скорость которой в данный момент времени равна нулю.

Пусть в момент времени t точки А и В плоской фигуры имеют скорости и , не параллельные друг другу (рис.33). Тогда точка Р, лежащая на пересечении перпендикуляров Аа к вектору и Вb к вектору , и будет мгновенным центром скоростей так как .

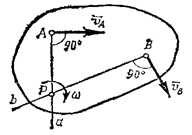
Рис.33 

Если теперь в момент времени взять точку Р за полюс, то скорость точки А будет , так как .Следовательно, скорости точек плоской фигуры определяются в данный момент времени так, как если бы движение фигуры было вращением вокруг мгновенного центра скоростей. При этом

Из равенств, следует еще, что точек плоской фигуры пропорциональны их расстоя­ниям от МЦС.

Полученные результаты приводят к следующим выводам.

1. Для определения мгновенного центра скоростей надо знать то­лько направления скоростей и каких-нибудь двух точек А и В плоской фигуры (или траектории этих точек);

2. Для определения скорости любой точки плоской фигуры, надо знать модуль и направление скорости какой-нибудь одной точки А фигуры и направление скорости другой ее точки В.

3. Угловая скорость плоской фигуры равна в каждый данный момент времени отношению скорости какой-нибудь точки фигуры к ее расстоянию от мгновенного центра скоростей Р:

.