Решение:

Пусть PB – x, тогда затраты на перевозку сырья из N в А пропорциональны

L_NP=334,86

y = 454,3 + 334,86 = 789,16

С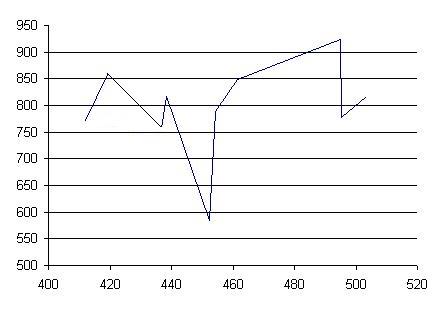 троим график по данным из группы:

Лекция.

Система массового обслуживания с ожиданием. Моделирование работы контейнерного терминала.

При моделировании будем полагать, что имеется N одинаковых каналов обслуживания (погрузки) прибывающих на автотранспорте контейнеров.

Интенсивность обслуживания заявок = μ, интенсивность входного потока заявок = λ, число заявок в очереди неограниченно.

График состояний системы обслуживания имеет вид:

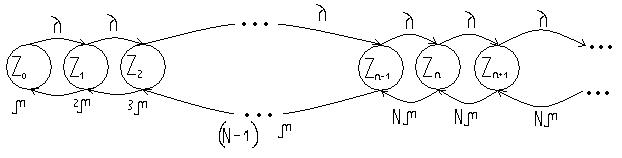
Составим систему дифференциальных уравнений Колмогорова и прировняем производные к 0, получим алгебраическую систему. Решив данную систему, получим значение финальные состояния вероятностей системы, которые в свою очередь позволяют рассчитать ряд других показателей эффективности системы.

Число свободных платформ под погрузку контейнеров.

Система показателя эффективности терминала имеет вид:

P_j – вероятность того, что из N каналов занято j каналов

- Все N-каналов заняты и какое-то число заявок находится в очереди.

- Все N-каналов свободны

- среднее число требований в очереди;

- коэффициент загрузки 1 канала, среднее число занятых каналов

- среднее число требований, находящихся в системе

- среднее время ожидания требований в очереди

- среднее время пребывания требований в системе

Планирование активного эксперимента с логистическими моделями. Полный факторный эксперимент (пфэ) типа 23

ПФЭ 2³ означает, что в исследовании варьируются 3 фактора и каждый из них принимает значение лишь на двух уровнях – нижнем и верхнем. В условиях рассматриваемых задач в качестве факторов используем λ, μ, N. Установим для них верхнее и нижнее значения.

Уровень фактора	X2 интенсивность поступления заявок на обслуживание - λ	Х3 – интенсивность обслуживания заявок - μ	Х4 – число каналов обслуживания – N
Нижний	1	1	1
Верхний	15	11	9

От реальных значений переменных для обеспечивания сопостовимости факторов перейдем к кодированию, при этом нижний уровень фактора получает значение -1, а верхний - +1.

Уровень фактора	X2 интенсивность поступления заявок на обслуживание - λ	Х3 – интенсивность обслуживания заявок - μ	Х4 – число каналов обслуживания – N
Нижний	-1	-1	-1
Верхний	1	1	1

Очевидно, что для кодирования переменных средний уровень каждого фактора = 0.

ПФЭ позволяет построить многофакторную линейную регрессионную модель вида:

y = b₁*x₁ + b₂*x₂+b₃*x₃+b₄*x₄+b₂₃*x₂₃+b₂₄*x₂₄+b₃₄*x₃₄+b₂₃₄*x₂₃₄

В данной модели x₁ = 1 – фиктивная переменная. Все остальные переменные (x₂, x₃, x₄) принимают либо верхнее, либо нижнее значение, которое для кодирования переменных равно -1 или +1.

Полным данный эксперимент называется потому, что для построения регрессионной модели (определения коэффициента b_j) используется полный перебор вариантов значений х₂, х₃, х_4.

Матрица планирования ПФЭ имеет вид:

n – номер эксперимента	X1	X2	X3	X4	X24	X23	X34	X234	Y
1	+	+	+	+	+	+	+	+	0
2	+	+	+	-	-	+	-	-	1,86
3	+	+	-	+	+	-	-	-	0
4	+	-	+	+	-	-	+	-	0
5	+	+	-	-	-	-	+	+	-64,3
6	+	-	-	-	+	+	+	-	0
7	+	-	+	-	+	-	-	+	0
8	+	-	-	+	-	+	-	+	0

Y рассчитывается так:

x₂ = λ = 15

x₃ = μ = 11

x₄ = N = 9

- вероятность того, что занято 0 каналов, т.е система свободна.

Y =

Аналогично рассчитываются Y₂, Y₃, Y₄, Y₂₃, Y₂₄, Y₃₄, Y₂₃₄

Практика.

Моделирование и оптимизация элементов логистической инфраструктуры. Определение оптимальных параметров емкости для перевозки сыпучих грузов.

Требуется найти угол α, обеспечивающий максимальный объем емкости для перевозки сыпучих грузов, устанавливаемой на железнодорожных платформах.

Поперечное сечение емкости – трапеция. Меньшее основание – a, боковая сторона – 2а.

а = 4,1 метра