1)Графоаналитический метод

Найти α , доставляющий минимум функции t=t(f) , t=t(α)

T= +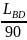

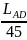
А-М

Д

С

В

А

l_AD=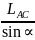 l_BD=l_BC-l_DC

l_BC=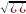 = =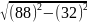81,98

tgα=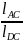 =81,98- =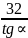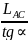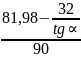

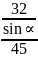
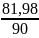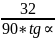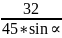T= + - + =T

α	10	20	30	40	50	60	70	80
T	3,11	2,01	1,72	1,6	1,53	1,52	1,54	1,57

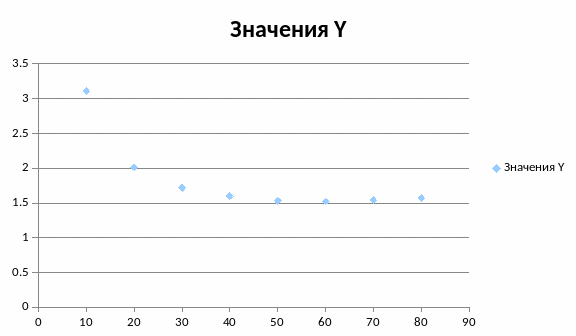
Выбираем вариант α=60 градусов

Практика

Условная оптимизация. Метод неопределенных множителей Лонградж.

Пусть у(Х)=f(х1, х2..х_n) и q(x)=q(x1, x2..x_n)-дважды непрерывно-дифференциальные скалярные функции векторного агрумента Х(х1,х2..х_n )

Требуется найти экстремум функции у(Х)при условии:

q_i(x1,x2..x_n)=0 i=1

Алгоритм метода множителей Лонграджа:

1)составляем функцию Лонграджа

L(x,Ʌ)=L(x1,x2..x_n;Ʌ1,Ʌ2..Ʌn)=f(x1,x2..x_n)+Σ(x_i;q_i(x1,x2..x_n))

L-функция Лонграджа

Ʌ-множитель Лонграджа

2)находим частные производные функции Лонграджа по (х1, х2..х_n;Ʌ1,Ʌ2..Ʌn)

Частные производные приравниваем к нулю

3)решаем полученную систему уравнений, находим стационарные точки значения функции

У(х1,х2..хn) в стационарных точках сравниваются между собой и определяем экстремумы

Пример: с целью определения типов машин, которые модно разместить в тоннеле, габаритные размеры машины ри этом должны выполнять следующие условие: зазоры между стенками тоннеля и техникой должны быть не менее заданной ∆.

Тоннель имеет диаметр-ρ

Решение:

ρ

Х22

С формальной точки зрения найти длину стороны квадрата х1, х2 максимального размера вписан в круг радиусом r=ρ-∆

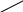
r

∆

Х1

В рассматриваемом случае f(х1, х2..х_n)=y=4x1*x2

Q(x1,x2)= + -

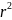
Cоставим функцию Лонграджа:

L(x1,x2;Ʌ)=4x1*x2+Ʌ( + - )

В данном выражении Ʌ-неопределенный множитель Лонграджа

Найдем частные производные от L по (х1,х2..Ʌ) и приравняем их к 0.

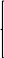dL(dx1)=4x2+2Ʌx1=0

dL(dx2)=4x1+2Ʌx2=0

dL(dɅ)= + =

4x2=-2Ʌx1

4x1=-2Ʌx2

+ =

4x2( -4)=0 4x2+2Ʌx1=0 4x2+4x1=0

-4=0 4x1+2Ʌx2=0 4x1+4x2=0

Ʌ=±2 + = + =

4x2-4x1=0

X1=x2

2 =

X1,x2=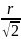

Лекция.

Формализация логистических систем.

ФЛС с использованием модели систем массового обслуживания. Модель сложной системы в общем случае характеризуется множеством величин, описывающих функционирование реальной системы и образующих следующие подмножества:

1)совокупность вводных воздействий на систему x_i принадлежащая Х

2)совокупность внутренних параметров системы d_j принадлежащей D

3)совокупность воздействий внешней среды v_i принадлежащей V

4)совокупность выходных характеристик системы y_r принадлежащей Y

Входные воздействия, воздецствия внешней среды, его внутренние параметры системы обычно считают независимыми и называют экзогенными переменными.

Выходные характеристики – зависимые и эндогенные.

Процесс функционирования системы описывается оператор Ф , который преобразует экзогенные переменные в эндогенные.

У=Ф(Х, D,V,T)

Данное соотношение- наиболее точное описание системы с учетом времени , поскольку в модели учитывается время- динамическая система. Множество векторов Z значение параметра динамической системы-пространство состояния системы.

Пусть Z=(Z1,Z2,Z3)

Z3

Введем пространство состояний системы

t

Z2

Z1

Z1=X

Z2=D

Z3=V

Траектория перехода системы из одного состояния в другое . Если к пространству состояния системы добавить время- фазовое пространство.

Динамическая система как математический объект содержит в своем описании модели :модель изменения состояний под воздействием внутренних причин; модель приема входного сигнала и изменения состояния под сигналами; модель формирования входного как реакция динамической системы на внутренние и внешние причины изменения состояния .

Простейшим примером динамической системы является одноканальная система массового обслуживания с отказами.

Граф состояния данной системы можно представить в виде

Z0 Z1

Z0-канал обслуживания свободен

Z1-занят канал обслуживания

Процесс функционирования данной системы описывается уравнением Колмагорова в левой части каждого уравнения должен стоять производная вероятности состояния.

Po(t)+p1(t)=1

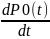=M-(Ʌ-M)P0(t)-(Ʌ+M)*t

P0(0)=1 p1(0)=0

P0(t)=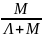 + *E

P1(t)= (t-

А правая часть должна содержать столько членов , сколько стрелок связано с данным состоянием.

Если стрелка отправлена из состояния, то соответственно член имеет отрицательный знак, а если в состояние, то знак +. Каждый член равен произв. Интенсивности перехода соответствующей данной стрелке и вероятности того состояния, из которого исходит стрелка.

Решение:

Лямда- интенсивность перехода из 0 в 1

М- интенсивность перехода из 1 в 0

Составим уравнение Колмагорова

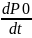=-ɅP0+Mp1

P0+p1=1

=-ɅP0+Mp0+M

=M-(Ʌ+M)*p0

В зависимости от соответствующих Ʌ и М возможны 3 случая:Ʌ>М, Ʌ<М, Ʌ=М

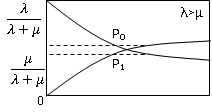
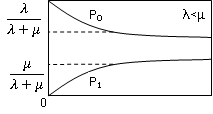
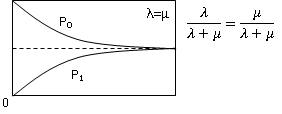
Как следствие рисунков значение вероятностей р0 и р1 при t>∞

Сходятся к константам, при этом

Р0=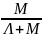

Р1=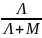

Рассмотренная модель –система массового обслуживания.

СМО-математические модели систем поступающих через случайные промежутки времени, длительные обслуживания-случайны.

Телефонный звонок, доставка груза на склад автомобиля, работа АЗС И ТД.

Канал обслуживания- устройство, способное в течение некоторого времени обслужить лишь одно требование.

Практика.

Оптимизация элементов в логистической инфраструктуре.

Для доставки продукции завода N в город А строится шоссе NP, соединяющее завод с железной дорогой AB, проходящей через город А. Стоимость перевозок по шоссе вдвое больше, чем по железной дороге. К какому пункту Р нужно провести шоссе, чтобы общая стоимость перевозок в город А по шоссе и по железной дороге была наименьшей.

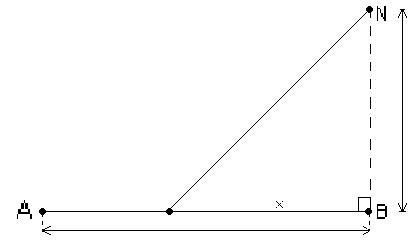
NB=145

AB=538