Геометрический подход к решению задач лп.

ГП имеет весьма ограниченное применение и используется для наглядной иллюстрации смысла существа подобных задач согласно геометрическому подходу область определения переменных задачи ЛП представляется в виде многоугольника, располагается в первой квадрате системы координат.

Экстремум целевой функции находится в вершине, а ее координаты соответствуют оптимальному решению.

Рассмотрим задачу:

Предприятие выпускает три вида тары в количествах:

В1-700 ед. тары 1-го вида

В2- 800 ед. тары 2-го вида

В3-600 ед. тары 3-го вида

Тара необходима для транспортировки на два региональных рынка двух наборов товаров.

Отправка 1-ой партии каждого набора требует слд. Расхода тары.

Вид тары	Вид заказа(набора)
	1	2
1	4	3
2	2	2
3	2	5

Рыночный спрос на одну партию первого вида 6 ден.ед

Требуется определить объем реализации на рынке партии товара из набора каждого, обеспечивающего макс. Прибыли его производителю, а также расход тары каждого вида на них.

Геометрического решение задачи:

1)постановка задачи: найти х1, х2 , доставляющие макс целевой функции

W=8х1+6х2

При ограничениях:

4х1+3х2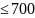

2х1+2х2≤800

2х1+5х2≤600

Х1≥0, х2≥0

2)от линейного неравенства перейдем к решению

4х1+3х2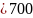

2х1+2х2=800

2х1+5х2=600

3)выразить х2 через х1 в каждом уравнении

Х2=(700-4х1)/3

Х2=(800-2х2)/2

Х2=(600-2х1)/5

4)строим график

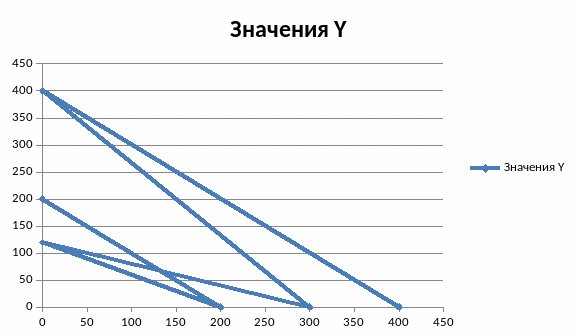
Примечание: Прямые линии, построенные в границах по уравнению факторного пространства могут пересекаться или находиться одна на другой . Согласно основному положению линейного программирования на полученном рисунке выделяется многоугольник , представляет собой область определения переменных х1, х2.

W1-0

W2-720

W3-1280

W4-1600

Практика.

Оптимизация фрагментов в логистической инфраструктуре.

Контактный провод для электропоездов имеет точки подвеса на двух столбах (расположенных на расстоянии 20 м друг от друга), прогиб провода соответствует параболе а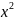 +вх+с , на расстоянии 2 м от левого столба, прогиб провода составил 9 см

Требуется установить величину прогиба посредине между столбами и принять решение о необходимости приведения данного параметра 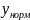=20 см

Решение задачи:

а +вх+с

0=а*0²+в*0+с с=0

0=а*20²+в*20+с

А*2²+в*2+с=-0,09

400а+20в=0 в=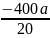 =-20а

4а+2в=-0,09

4а+2(-20а)=-0,09

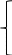А=0,0025

В=-0,05

С=0

Х=10

У=0,0025*(10)²+(-0,05)*10+0

У=-0,25=- 25 см

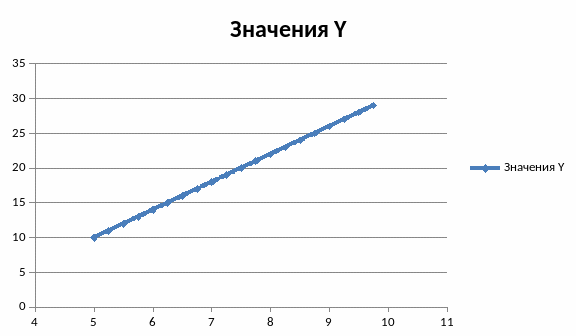
Вывод: прогиб не соответствует норме( 20 см), нужно подтянуть на 5 см.

Строим обобщенный график:

Лекция.

Линейное программирование .

Симплекс-метод.

Решение задачи ЛП.

Симплексный метод, в отличие от геометрического универсален. С его помощью можно решить любую задачу ЛП.

Применение симплекс-метода осуществляется в 2 этапа:

Нахождение исходного допустимого решения.

Последовательное улучшение полученного решения до оптимального .

Основные операции симплекс-методы найдем с использованием индивидуального вида задания.

Постановка задачи:

Этап 1.

Найти х1, х2 доставляющие max W=8х1+6х2

При ограничениях :

4х1+3х2≤700

2х1+2х2≤800

2х1+5х2≤600

Х1≥0

К ограничениям равенства введем дополнительные переменные

Х3, х4, х5

4х1+3х2+х3=700

2х1+2х2+х4=800

2х1+5х2+х5=600

Нахождение допустимого базисного решения за основным переменные примем х3, х4, х5; х1,х2- неосновные

Примечание: неосновные=0

Получено допустимое, исходное, базисное решение

(х1,х2,х3,х4,х5)=(0,0,700,800,600)

Очевидно, что с точки зрения здравого смысла данное решение не оптимально поскольку W=8х1+6х2=0 ; воспользуемся формальным критерием оптимальности: если в выражении целевой функции имеется хотя бы 1 переменная с положительным коэффициентом , то полученное решение нельзя признать оптимальным, в нашем случае обе переменные имеют коэффициенты с положительным знаком, следовательно допустимое базисное решение надо улучшить.

Этап 2.

Улучшение допустимого исходного базисного решение до оптимального.

Этап представляет собой блок операций:

2.1 в выражении W=8х1+6х2 выбираем переменную с максимально-положительным коэффициентом , ее как обеспечивающую максимальное приращение W следует перевести в основные

2.2 определяем основную переменную , которая вместо х1 становится неосновной; для этого из условия не отрицательности переменной

Х3=700-4х1-3х2

Х4=800-2х1-2х2

Х5=600-2х1-5х2

Х1=min(175, 400,300)= 175

Поскольку х1 найдено с использованием первого уравнения, то в неосновные переменные должна быть переведена х3

2.3 запишем новое решение, с этой целью используем х3= 700-4х1-3х2

Выразим х1 через другие переменные и полученное выражение для х1 подставим в остальные уравнения

1. Х1=175-0,75х2-0,25х3

2. 2)Х3=700-4(175-0,75х2-0,25х3)

-3х2

3. Х4=800-2(175-0,75х2-0,25х3)

-2х2

4. Х5=600-2(175-0,75х2-0,25х3)

-5х2

W=8(175-0,75х2-0,25х3)+6х2

W=1400-2х3

(х1,х2,х3,х4,х5)=(175, 0, 0, 450,250)

Интерпретация решения: набор 2,3 не следует делать.

Практика.

Моделирование и оптимизация элементов логистической инфраструктуры.

Населенный пункт А расположен на расстоянии 32 от автомагистрали, 88 от города В, через которых проходит магистраль.

Под каким углом к автомагистрали нужно построить подъездную дорогу, чтобы затраты времени на А>В были минимальны, если допустимая скорость движения по магистрали 90 км/ч, а по объездной 45 км/ч.

Решение: