
- •Лекция .
- •Лекция.
- •Метод наименьших затрат
- •5)Рассчитываем весовые коэффициенты маршрутов по показателям
- •Геометрический подход к решению задач лп.
- •1)Графоаналитический метод
- •Решение:
- •Планирование активного эксперимента с логистическими моделями. Полный факторный эксперимент (пфэ) типа 23
- •Решение:
Метод наименьших затрат
Х11 Х12 Х13 0 90 30
Х21 Х22 Х23=10 0 90
Х31 Х32 Х33 80 0 0
W=90*6+4*30+10*3+90*5+2*80=1300
Если запросы потребителей оказались больше возможностей поставщиков, то вводим фиктивного поставщика с возможностями равными разнице между числами. Если возможности оказались больше, то вводим потребителя.
Практика .
Самостоятельная работа.
Методы безусловной оптимизации.
Требуется сравнить 14 возможных маршрутов из 1 в 10 пункт по трем показателям: W1- дальность, W2-безопасность, W3-средняя допустимая скорость
Решение:
Вариант маршрута |
W1 |
W2 |
W3 |
М1 |
380 |
0,80 |
195 |
М2 |
400 |
0,81 |
100 |
М3 |
420 |
0,84 |
105 |
М4 |
420 |
0,88 |
105 |
М5 |
380 |
0,85 |
95 |
М6 |
360 |
0,88 |
90 |
М7 |
400 |
0,88 |
100 |
М8 |
400 |
0,91 |
100 |
М9 |
420 |
0,82 |
105 |
М10 |
400 |
0,83 |
100 |
М11 |
400 |
0,88 |
100 |
М12 |
400 |
0,91 |
100 |
М13 |
420 |
0,88 |
105 |
М14 |
400 |
0,88 |
100 |
-
показатель
W1
W2
W3
ранг
3
1
2
2)рассчитать весовые коэффициенты показателей по формуле
Wj |
W1 |
W2 |
W3 |
Cj |
1/3 |
1 |
2/3 |
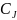 =1-
=1-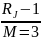
|
W1 |
W2 |
W3 |
|
1/6 |
1/2 |
1/3 |
4)проранжируем маршруты по каждому показателю
Wj |
М1 |
М2 |
М3 |
М4 |
М5 |
М6 |
М7 |
М8 |
М9 |
М10 |
М11 |
М12 |
М13 |
М14 |
W1 |
12,5 |
7 |
2,5 |
2,5 |
2,5 |
1 |
7 |
7 |
2,5 |
7 |
7 |
7 |
2,5 |
7 |
W2 |
14 |
13 |
10 |
5,5 |
9 |
5,5 |
5,5 |
1,5 |
12 |
11 |
5,5 |
5,5 |
5,5 |
5,5 |
W3 |
12,5 |
8 |
2,5 |
2,5 |
12,5 |
14 |
8 |
8 |
2,5 |
8 |
8 |
8 |
2,5 |
8 |
5)Рассчитываем весовые коэффициенты маршрутов по показателям
=1-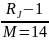
Wj |
М1 |
М2 |
М3 |
М4 |
М5 |
М6 |
М7 |
М8 |
М9 |
М10 |
М11 |
М12 |
М13 |
М14 |
W1 |
0,90 |
0,57 |
0,18 |
0,18 |
0,90 |
1 |
0,57 |
0,57 |
0,18 |
0,57 |
0,57 |
0,57 |
0,18 |
0,57 |
W2 |
0,07 |
0,14 |
0,36 |
0,68 |
0,43 |
0,68 |
0,68 |
0,96 |
0,21 |
0,28 |
0,68 |
0,96 |
0,68 |
0,68 |
W3 |
0,18 |
0,5 |
0,90 |
0,90 |
0,18 |
0,07 |
0,5 |
0,5 |
0,90 |
0,5 |
0,5 |
0,5 |
0,90 |
0,5 |
Wj |
М1 |
М2 |
М3 |
М4 |
М5 |
М6 |
М7 |
М8 |
М9 |
М10 |
М11 |
М12 |
М13 |
М14 |
W1 |
0,12 |
0,076 |
0,024 |
0,024 |
0,12 |
0,133 |
0,076 |
0,076 |
0,024 |
0,076 |
0,076 |
0,076 |
0,024 |
0,076 |
W2 |
0,09 |
0,08 |
0,048 |
0,09 |
0,057 |
0,09 |
0,09 |
0,128 |
0,21 |
0,037 |
0,09 |
0,128 |
0,09 |
0,09 |
W3 |
0,024 |
0,06 |
0,12 |
0,12 |
0,024 |
0,09 |
0,06 |
0,06 |
0,12 |
0,06 |
0,06 |
0,06 |
0,12 |
0,06 |
6)нормируем весовые коэффициенты маршрутов по каждому показателю
7)рассматриваем значения обобщенный показатель конкурентоспособности маршрутов, по результатам составляем рейтинг наиболее конкурентоспособного маршрута
Маршрут |
ОП |
Рейтинговая оценка |
М1 |
0,073 |
6/2 |
М2 |
0,073 |
6/2 |
М3 |
0,068 |
7 |
М4 |
0,089 |
4/2 |
М5 |
0,0565 |
8 |
М6 |
0,295 |
2 |
М7 |
0,078 |
5/3 |
М8 |
0,673 |
1/2 |
М9 |
0,149 |
3 |
М10 |
0,052 |
9 |
М11 |
0,078 |
4/3 |
М12 |
0,673 |
1 /2 |
М13 |
0,089 |
4/2 |
М14 |
0,078 |
5/3 |
Лучшие маршруты: М8, М12.
Практика .
Классические задачи оптимизации.
Оптимизация-
выбор наилучшего варианта из множества
возможных. Выделяют группу классических
или задач на безусловный экстремум.
Общая постановка этих задач: найти
вектор X=(x1,
x2.. ).
При котором достигается наибольшее или
наименьшее значение непрерывной,
скалярной , дифференциальной функции
f(x).
).
При котором достигается наибольшее или
наименьшее значение непрерывной,
скалярной , дифференциальной функции
f(x).
В основе методов лежит теория дифференциального исчисления.
Задача 1.
Исследовать
на экстремум функцию y=
2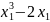 *
*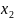 +
+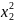
Решение:
 Найдем
стационарные точки функции из условия
Найдем
стационарные точки функции из условия
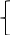
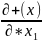 =0
6
=0
6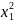 -2
-2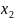 =0
=0
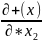 =0
-2
=0
-2 +2
=0
+2
=0
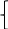
 Х1=
0 Х2=0
Х1=
0 Х2=0
Х1=1/3 Х2=1/3
Найдены две стационарные точки:
А(0,0)
В(1/3,1/3)
Проверим, являются ли эти точки точками экстремума, для этого составим матрицу Гессе и вычислим ее значение в точке А.

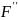 (x)=
(x)=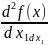
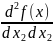 = 12
= 12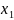 2
2
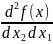
 -2
+2
-2
+2
Вычислим главные диагональные миноры матрицы Гессе:
М1=2
М2=12 =0
Правило : Для того, чтобы F(x) имела в стационарных точках локальный минимум необходимо в этой точке все главные диагональные миноры были положительны.
Для локального максимума необходимо чтоб у матрицы Гессе главные диагональные миноры нечетной степени были отрицательны, а миноры четных положительны.
Точка А не является точкой экстремума функции составим матрицу Гессе в точке В.
М1=2
М2=4
Точка В-Локальный минимум
Хmin=(1/3,1/3) при этом значении F(x)= - 1/27
Задача 2.
Y=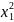 -
*
+
+9
-6
+20
-
*
+
+9
-6
+20
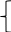 2
-
+9=0
2
-
+9=0
- +2 -6=0
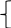 X1=-4
X1=-4
X2=1

 (x)=
2 2 М1=-1
(x)=
2 2 М1=-1
-1 -1 М2=2
Y=1+2+4-9-12+20=6
Локальный максимум Хmax=(-4,1)
Лекция
Метод Потенциалов
Мы получили на предыдущей лекции оптимальный план перевозок с наименьшими затратами , но является ли он оптимальным?
|
90(В1) |
90(В2) |
120(В3) |
120(А1) |
7 |
|
|
100(А2) |
|
8 |
|
80(А3) |
|
3 + |
7 |
МП:
Каждому поставщику поставим в соответствии
потенциалы А, а потребителю- В. Один из
потенциалов (А1=0).
 =Ai+Bj-
запишем данное соотношение для всех
заполненных клеток
=Ai+Bj-
запишем данное соотношение для всех
заполненных клеток
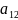 =6,
=6,
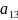 =4,
=4,
 =3,
=3,
 =5,
=5,
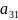 =2.
Аналогичную систему напишем для всех
незаполненных клеток( псевдоклетки):
=2.
Аналогичную систему напишем для всех
незаполненных клеток( псевдоклетки):
 =2,
=2,
 =7,
=7,
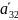 =6,
=6,
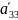 =4.
Условием оптимального плана является
=4.
Условием оптимального плана является
 -
-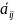 >0
>0
 >0
>0
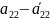 >0
>0
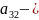 <0-
план не оптимален
<0-
план не оптимален
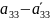 >0
>0
Если отрицательных разниц несколько , то улучшение плана начнется с максимальной разницей по модулю. Улучшение клетки с 3,2.
Улучшение плана состоит в перераспределении объемов перевозок между участниками и сводится к следующему: строится цепь пересчета , цепь имеет форму прямоугольной фигуры , одна из вершин данной фигуры находится в свободной клетке с отрицательной разностью(на рисунке выделено), а остальные вершины в заполненных клетках. Все углы в данной фигуре прямые. В одной строке не должно быть более двух вершин. Всем вершинам предписываются чередующиеся знаки (+ - добавить, - вычесть). Из клеток со знаком минус выбирается наименьшая величина груза и последовательно перемещается из клетки в клетку по построенной цепи.
 0
10 110
0
10 110
90 0 10 =W= 7*0+6*10+4*110+90*3+8*0+5*10+0*2+80*3+0*7=1060
10 80 0
Практика .
Методы программирования с фиктивным поставщиком.
Метод наименьших затрат W=1362
|
98 |
97 |
123 |
121 |
7 |
|
|
106 |
|
8 |
|
84 |
|
3 |
7 |
7 |
|
0 |
0 |
Метод «северо- западного угла» W= 2164
|
98 |
97 |
123 |
121 |
|
|
|
106 |
|
|
|
84 |
|
3 |
|
7 |
|
0 |
|
План перевозок , полученный метод наименьших затрат оказался оптимальным, проверим его методом потенциалов, изученный ранее.
Запишем для всех заполненных клеток отношение =Ai+Bj
=6,
=4,
=3,
=5,
=2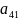 =0
=0
Теперь
для псевдоклеток
=2,
=7,
=6,
=4,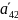 =4,
=4,
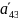 =0
=0
 >0,
>0,
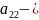 >0,
>0,
 <0,
<0,
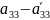 >0,
>0,
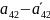 <0,
<0,
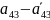 >0
>0
|
98 |
97 |
123 |
121 |
7 |
|
|
106 |
|
8 |
|
84 |
|
3 |
7 |
7 |
|
+ |
0 |
W=0*7+90*6+31*4+3*14+0+92*5+2*84+0+0+0+7*0+0=1332
Лекция .
Методы динамического программирования.
ДП(Динамическое Программирование)- особый метод оптимизации решения, специально приспособленное к многошаговым операциям.
Любую многошаговую задачу можно решить по-разному либо сразу искать все решения на всех шагах , либо строить оптимальное управление шаг за шагом.
Обычно второй способ оптимизации оказывается проще первого особенно при большом числе шагов.
Идея такой постепенной пошаговой оптимизации лежит в основе метода ДП.
Оптимизация первого шага проще оптимизации всего процесса.
Планируя многошаговую операцию выбирают управление на каждом шаге с учетом всех будущих исходов на предстоящих шагах.
Процесс ДП разворачивается от конца к началу , т.е. шаг сначала планируем последний.
Пример: Строй орг получила подряд на сооружение трубопровода А-В по пересечении местности п В лежит к северо-восток от А из тех условий прокладка трубопровода состоит в совершении ряда шагов ,при этом, на каждом шаге можно двигаться либо на север или восток. Любой путь А-В представляет собой ступенчатую ломанную. Затраты на сооружение каждого объекта известны, требуется проложить путь нефтепровода из А в В таким образом , чтобы суммарные затраты были минимальны: 1)Условная оптимизация на маршруте из В в А,2) Безусловная оптимизация.
85
16
28
76
466
51
97





19
41
37
39
37
16
16
23
32
11
68
19
23
88
14
51
94
35
77
18
34
87
122
157























Лекция .
Оптимизация управленческих решений в условиях неопределенности стохастического характера.
Основная особенность рыночной экономики-стихийная финансовая экономическая деятельность хозяйственных субъектов.
Риск-возможность не достичь целей бизнеса. Для нивелированных(Нивелирование — определение разности высот двух или многих точек земной поверхности относительно условного уровня (напр., уровня океана, реки и пр.), то есть определение превышения) рисков используют подходы: страхование проекта, распределение риска между участниками, уход от риска. Часто факторы риска- нечисловые переменные. Вместе с тем в моделях логистических проектов, процессов, систем используется большое количество числовых показателей: издержки, прибыль, объемы. По своей природе все они случайные величины , распределение которых согласно центр. предел. теории Ляпунова подчинены закону Гаусса. В этой связи исследование операций с подобными факторами: фактор стохастической природы- осуществляется в рамках теории вероятностей и математической статистики.
Основы
ТЕОРИИ ВЕРОЯТНОСТЕЙ:
Случайные
факторы –факторы, характеризующиеся
вероятностными распределениями. СФ
проявляются в виде случайных событий,
величин, процессов. В практике научное
исследование имеет место не воспроизводство
в том смысле, что повторное их проведение
при неизменном комплексе условий дает
различные результаты , исходы подобного
эксперимента характеризуются наблюдаемой
переменной , наблюдаемая переменная
включает множество всех взаимоисключающих
исходов экспериментов. Е- достоверное
множество, невозможное множество(пустое)-
Ø. В практике ИО широко используется
понятие мат. ожидание случайной величины
х , которая является средним значением
х. Данную величину рассчитывают с
использованием выражения M[x]=Σ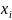 P(
)
-значение
случайной величины Х, P(
)-
вероятность этого значения, M[x]-
средняя величина прибыли за весь
период.По практике ИО в условиях
стохастической неопределенности для
выбора того или иного проекта используют
критерии максимума среднего результата,
если имеется ряд проектов с различными
M[x]
, то выбирается проект с наибольшим M[x]
и с наименьшим M[x]
если это издержки. D[x]=Σ(
-M[x])2P(
),
СКО=
P(
)
-значение
случайной величины Х, P(
)-
вероятность этого значения, M[x]-
средняя величина прибыли за весь
период.По практике ИО в условиях
стохастической неопределенности для
выбора того или иного проекта используют
критерии максимума среднего результата,
если имеется ряд проектов с различными
M[x]
, то выбирается проект с наибольшим M[x]
и с наименьшим M[x]
если это издержки. D[x]=Σ(
-M[x])2P(
),
СКО=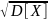 .
Именно D
является характеристикой рисков бизнеса
чем меньше дисперсия, тем меньше риск.
.
Именно D
является характеристикой рисков бизнеса
чем меньше дисперсия, тем меньше риск.
Пример
Пусть некоторое лицо выбирает один из двух вариантов инвестиционного проекта а и в , возможны следующие случаи:
1)Ма=Мв Да<Дв, средняя прибыль по проектам одна и та же, но дисперсия у проекта а<в
2)Ма>Мв Da<Db , выбираем а
3)Ma>Mb Da=Db, выбираем а
4)Ma>Mb Da>Db, неопределенность
5)Ма<Mb Da<Db,неопределенность
Данные виды неопределенностей разрешаются на основе выбора лица, если он осторожен и не жаден то а (4).
Практика .
Оптимизация решений в условиях стохастической неопределённости.
В дирекции предприятия принято решение вложить свободные средства по созданию транспортно-складской логистической системы. Требуется оценить риск потери инвестиций и выбрать оптимальный проект с точки зрения минимального риска.
Факторы риска ФР1-пожар, ФР2-креминогенный риск, ФР3-банкротство страховщика, ФР4- нарушение режима перевозок, ФР5- невыполнение технико-технологических требований, транспорт и хранение продукции, ФР6-природно- климатические катаклизмы, ФР7- отказ транспортных средств и оборудований, ФР8- нарушение работы транспортной и технической инфраструктуры, ФР9- риск ущерба от непрофессиональных действий персонала, ФР10- несвоевременная поставка грузов и оборудования, ФР11- появление новых конкурентов, ФР12- нарушение контрактов партнеров, ФР13- срыв финансирования проекта, ФР14- изменение цен на товары и услуги, ФР15-другие.
1)Оценим в баллах или в процентах от планирования прибыли максимальный ущерб от каждого из выявленных видов риска
ФР1 |
ФР2 |
ФР3 |
ФР4 |
ФР5 |
ФР6 |
ФР7 |
ФР8 |
ФР9 |
ФР10 |
ФР11 |
ФР12 |
ФР13 |
ФР14 |
ФР15 |
67 |
41 |
18 |
35 |
84 |
75 |
11 |
98 |
27 |
50 |
15 |
66 |
88 |
24 |
49 |
Максимальный ущерб-100% Минимальный ущерб- 0%
2)С использованием экспертного анализа проранжировать риски с точки зрения возможности (вероятности) наступления, 3)далее рассчитываем весовые коэффициенты факторов, 4)после нормируем значения коэффициентов их суммой
Значение таблицы 4 можно интерпретировать как субъективную версию событий , приводящих к ущербу. Рассчитываем числовые значения обобщенных показателей риска, как математическое ожидание ущерба. Данный показатель представляет сумму попарных произведений .
ОПР= ФР1(Т1)*ФР1(Т4)+ФР2(Т1)*ФР2(Т4)…+ФРn(Т1)*ФРn(Т4)
Инвестор может не получить из-за негативных событий, связанных с риском по данному показателю с использованием множество альтернативных проектов по критерию наименьшего результата можно выбрать опт. проект.
Лекция .
Статистическая методы в задачах оптимизации УР.
Туристическая поездка в выходной день на общ. ж/д транспорте часто связана с выбором направления поездки. Данный выбор обусловлен тем, насколько удобными является расписание движения поездов. Основными требованиями при этом являются максимальное число поездов в день поездки и равномерное распределение их в расписании.
В данной задаче дано расписание движения. Далее распределяем решением задачи подъем все моменты отправления поездов по 7-м интервалам от 4 до 25. Точками над числовой осью пометить поезда приходящие на каждый интервал.
Для решения задачи воспользуемся следующими показателями.
W1- общее число поездов
W2- относительное отклонение числа поездов, приходящихся на один интервал при равномерном законе распределения
W3-максимальная величина интервала (перерыва между поездами в расписании)
W4-дисперсия интервала времени между поездами
Сначала для этого находим мат. Ожидание
 =
=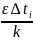
K- сумма перерывов (кол-во)
 -сумма
перерывов по времени
-сумма
перерывов по времени
D=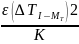
Wj |
M1 |
W1 |
|
W2 |
|
W3 |
|
W4 |
|
W5 |
|
W1-чем больше, тем лучше; W2,W3,W4-чем меньше , тем лучше
Практика.
Метод стохастической оптимизации.
 Данная
процедура относится к разряду аналитических
градиентов методов. Воспользуемся
примером курса классическая безусловная
оптимизация: требуется найти min
функции
Данная
процедура относится к разряду аналитических
градиентов методов. Воспользуемся
примером курса классическая безусловная
оптимизация: требуется найти min
функции
 .
Воспользуемся последовательным
симплексным методом, но с той разницей,
что отражение симплекса на каждом шаге
происходит случайным образом. Пусть
ребро симплекса l=0,2.
Центр тяжести исходного симплекса
определяется с помощью случайных чисел:
0,58 — х1,
0,35 — х2.
Шаг 0.
.
Воспользуемся последовательным
симплексным методом, но с той разницей,
что отражение симплекса на каждом шаге
происходит случайным образом. Пусть
ребро симплекса l=0,2.
Центр тяжести исходного симплекса
определяется с помощью случайных чисел:
0,58 — х1,
0,35 — х2.
Шаг 0.
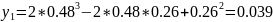 3
— наибольшее
3
— наибольшее
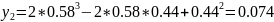 1
— наименьшее
1
— наименьшее
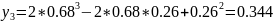
yj |
||
1 |
2 |
3 |
0.039 |
0.074 |
0.344 |
Ранги |
||
1 |
2 |
3 |
Вероятность |
||
0,17 |
0,33 |
0,5 |
0,61 — лежит в Р3 |
||
yj |
||
1 |
2 |
3 |
0.039 |
0.074 |
-0,031 |
Ранги |
||
2 |
3 |
1 |
Вероятность |
||
0,33 |
0,5 |
0,17 |
0,15 — лежит в Р1 |
||
yj |
||
1 |
2 |
3 |
0.457 |
0.074 |
0,171 |
Ранги |
||
3 |
1 |
2 |
Вероятность |
||
0,5 |
0,17 |
0,33 |
0,25 — лежит в Р1 |
||
yj |
||
1 |
2 |
3 |
0.457 |
0.074 |
0,344 |
Ранги |
||
3 |
1 |
2 |
Вероятность |
||
0,5 |
0,17 |
0,33 |
0,72 — лежит в Р3 |
||
yj |
||
1 |
2 |
3 |
0.457 |
0,093 |
0,171 |
Ранги |
||
3 |
1 |
2 |
Вероятность |
||
0,5 |
0,17 |
0,33 |
0,89 — лежит в Р3 |
||
yj |
||
1 |
2 |
3 |
0.007 |
0.074 |
0,171 |
Ранги |
||
1 |
2 |
3 |
Вероятность |
||
0,17 |
0,33 |
0,5 |
0,39 — лежит в Р2 |
||
yj |
||
1 |
2 |
3 |
0.457 |
0,093 |
0,125 |
Ранги |
||
3 |
1 |
2 |
Вероятность |
||
0,5 |
0,17 |
0,33 |
0,66 — лежит в Р2 |
||
yj |
||
1 |
2 |
3 |
0.457 |
0,15 |
0,125 |
Ранги |
||
3 |
2 |
1 |
Вероятность |
||
0,5 |
0,33 |
0,17 |
0,97 — лежит в Р3 |
||
yj |
||
1 |
2 |
3 |
0.457 |
0,15 |
0,5 |
Ранги |
||
2 |
1 |
3 |
Вероятность |
||
0,33 |
0,17 |
0,5 |
0,21 — лежит в Р1 |
||
yj |
||
1 |
2 |
3 |
0.156 |
0,15 |
0,5 |
Ранги |
||
2 |
1 |
3 |
Вероятность |
||
0,33 |
0,17 |
0,5 |
 Приближенное
значение min функции y=2x13-2x1x2+x22 для
установленных условий поиска (0,58; 0,35).
Увеличить точность поиска можно уменьшив
ребро симплекса.
Приближенное
значение min функции y=2x13-2x1x2+x22 для
установленных условий поиска (0,58; 0,35).
Увеличить точность поиска можно уменьшив
ребро симплекса.

Практика/Лекция.
Статистические методы в задачах оптимизации УР.
Расписание движения поездов имеет вид:
5:14; 5:30; 5:48; 6:13; 6:20; 6:35;6:38; 6:57; 7:05; 7:13; 7:24;7:40;7:45; 7:50; 7:55;8:00;8:07;8:12; 8:26; 8:35; 8:45;8:50;8:55; 9:18; 9:22; 9:36; 9:57; 10:07; 10:47; 10:58;11:04;11:15; 11:47; 13:57; 16:00; 16:30;16:43; 17:10; 17:27;17:45;18:04; 18:26; 18:44; 19:17; 19:39;19:55; 20:41; 21:20; 22:34; 23:10; 23:34;01:15
Решение задачи:

 Распределим
отправления по 7ми интервалам от 5 до
1:15. Точки — поезда, приходящие в каждый
интервал времени.
Распределим
отправления по 7ми интервалам от 5 до
1:15. Точки — поезда, приходящие в каждый
интервал времени.






Для решения задачи воспользуемся системой показателей:
W1 — число поездов в расписании. W1 = 54.
W2
— сред. линейное относит. отклонение
числа поездов в одном интервале при
равномерном законе движения поездов.
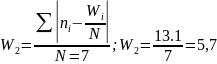
W3 — max величина интервала между поездами в расписании.

W4 — дисперсия интервала между последовательными поездами .
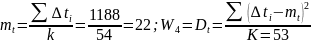 ,
,
где — сумма перерывов по времени, K— кол-во перерывов;
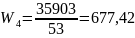
Аналогичные расчёты проводятся для всего множества поездов; составляется таблица рангов каждого направления по каждому показателю.
Wj |
Курский –Подольск |
Курский – Царицыно |
Павелецкий – Барыбино |
Москва –Петушки |
Рижский – Истра |
W1 |
47 |
54 |
38 |
16 |
30 |
W2 |
1,9 |
5,7 |
1,6 |
1,2 |
10 |
W3 |
130 |
130 |
70 |
153 |
131 |
W4 |
4045,86 |
677,42 |
259 |
1573,3 |
575,75 |
Wj |
Курский –Подольск |
Курский – Царицыно |
Павелецкий – Барыбино |
Москва –Петушки |
Рижский – Истра |
W1 |
2 |
1 |
3 |
5 |
4 |
W2 |
3 |
4 |
2 |
1 |
5 |
W3 |
2 |
3 |
1 |
5 |
4 |
W4 |
5 |
3 |
1 |
4 |
2 |
Σ |
12 |
11 |
7 |
15 |
15 |
Лекция.
Линейное программирование (ЛП). Геометрическое решение задач ЛП.
В
общей постановке задача ЛП состоит в
отыскании значений n
переменных, называемых х1, х2..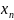 ,
доставляющих экстремум функции: W=ΣСi*Xi,
при условиях:
,
доставляющих экстремум функции: W=ΣСi*Xi,
при условиях:
а11*х1+а12*х2+..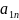 *
≤
*
≤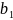
а21*х1+а22*х2+..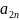 *
≤
*
≤
…………..
Αm1*x1+am2*x2+…+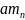 *
≤
*
≤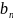
Для всех Xi≥0
Приведенная выше целевая функция, все условия- линейные(все переменные в первой степени), потому подобные задачи и называются задачи линейного программирования.
Решение задачи линейного программирования исходя из условий , не должно быть отрицательным, допустимым!
Допустимое решение, при котором функция принимает оптимальное значение- оптимальное решение.
Ограничение неравенства в задачах линейного программирования часто заменяют равенствами с дополнительной переменной в этом случае задача ЛП:
W=ΣСi*Xi,
при условиях:
а11*х1+а12*х2+..
*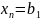
а21*х1+а22*х2+..
*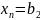
…………..
Αm1*x1+am2*x2+…+
*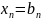
Для всех Xi≥0
Частное решение системы уравнения(условия ограничены), получаемое приравниванием нулю n называют базисным. При этом переменные приравниваемые нулю принято называть неосновными , оставшиеся- основными.
Оптимальное решение задачи линейного программирования ищут среди допустимых базисных решений. Для этого используют специфические условия задач ЛП, которые вводят эти свойства рядом теорем. Из них непосредственно следует справедливость слд положения- экстремум целевой функции является абсолютным, достигается хотя б в одной точке многогранника, задающего область определения задачи ЛП, данная точка соответствует допустимому базисному решению системы уравнений- ограничений. Для решения задач ЛП используют различные методы: геометрический метод, симплекс-метод, распределительный метод.

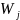
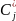

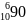 -
-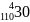 +
+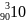 +
+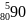 -
-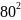 -
-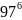
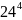
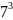
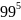
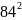

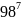
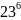

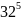
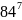
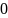

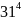
 +
+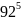
 -
-