
- •Лекция .
- •Лекция.
- •Метод наименьших затрат
- •5)Рассчитываем весовые коэффициенты маршрутов по показателям
- •Геометрический подход к решению задач лп.
- •1)Графоаналитический метод
- •Решение:
- •Планирование активного эксперимента с логистическими моделями. Полный факторный эксперимент (пфэ) типа 23
- •Решение:
Лекция .
Экономические основы исследования операций в логистике. Логистика как направление предпринимательской деятельности.
Исследование-получение новых знаний об изучаемом объекте.
Операция- системно-упорядоченная последовательность действий, приводящая к достижению целей.
В классическо-экономической теории были исследованы основные факторы производства:
Факторы производства |
земля |
капитал |
труд |
Предпринимательская активность |
Инновационно-информационный потенциал |
Форма дохода |
рента |
процент |
з/п |
прибыль |
Прибыль от интеллектуальной добавленной стоимости |
Логистика-наука и искусство управления, планирования, организации ресурсных потоков, направленное на оптимизацию всех процессов в производстве, достижении, снабжении потребностей потребителей и уменьшение издержек .
Особенностью логистики является, что она тесно связана с менеджментом и маркетингом. Управление логистическими процессами-менеджмент.
Существуют различные виды потоков: материальный, сервисный, информационный, финансовый, людской, и т.д.
Существуют различные логистические системы: концентрационные, эшелонированные, комбинированные, ,выталкивающие и т.д.
Логистическая эшелонированная система- логистическая система, в которой материальный поток на пути от производителя к потребителю проходит, по крайней мере, через одного посредника (дилера, дистрибьютора и др.).
В курсе «исследование операций» учитываются в дихотомической сфере : «да» или «нет» модели различных сочетаний уровней этих факторов (потребность/спрос/предложение/результат взаимодействия факторов для рынка ), 8 вариантов.
Практика
Тема: «Безусловная оптимизация. Метод Парето.
Wi |
T1 |
T2 |
T3 |
T4 |
T5 |
W1 |
10 |
5 |
1 |
3 |
9 |
W2 |
9 |
4 |
8 |
6 |
10 |
W3 |
6 |
9 |
7 |
10 |
3 |
W4 |
10 |
6 |
1 |
2 |
5 |
W5 |
7 |
6 |
8 |
1 |
10 |
W6 |
3 |
5 |
10 |
9 |
1 |
W7 |
10 |
9 |
3 |
1 |
5 |
W8 |
10 |
9 |
4 |
1 |
8 |
W9 |
10 |
1 |
9 |
8 |
2 |
W10 |
10 |
9 |
5 |
1 |
8 |
Оптимальным по Парето является вариант, для которого не существует другого варианта по всем показателям не хуже данного , а хотя бы по одному лучше. Реализуется с использованием таблиц попарного сравнения(если Т1 по первому показателю лучше Т2,то в первой клетке таблицы ставим +:если хуже ставим -, если равны 0. Вычеркиваются альтернативы ,по которым хотя бы в одной таблице нет -.
|
T1 |
T2 |
T4 |
T5 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
W1 |
- |
- |
- |
- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
W2 |
- |
+ |
+ |
- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
W3 |
+ |
- |
- |
+ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
W4 |
- |
- |
- |
- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
W5 |
+ |
+ |
+ |
- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
W6 |
+ |
+ |
+ |
+ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
W7 |
- |
- |
+ |
- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
W8 |
- |
- |
+ |
- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
W9 |
- |
+ |
+ |
+ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
W10 |
- |
- |
+ |
- |
Так же происходят сравнения Т4 и Т5 со всеми другими вариантами. В итоге получаем самые оптимальные варианты , судя по методу Парето.
Практика.
Методы безусловной оптимизации.
Последовательный симплексный метод.
ПСМ- графоаналитическая процедура поисков экстремума в многофакторных задачах оптимизации.
Симплекс- отрезок прямой в одномерном; в двумерном- правильно-равносторонний треугольник; в трехмерном- правильная треугольная пирамида.
Пример: Принято решение о строительстве горно-обогатительного комбината, даны координаты трех карьеров(К1(15;95)К2(99;19)К3(89;89), откуда вероятнее будут брать сырье, требуется определить координаты комбината из условия минимума стоимости перевозки сырья, стоимость перевозок 1-300 т/км, 2-250 т/км, 3-200 т/км.
Решение:
1.Опеределим центр тяжести исходного симплекса
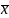 =
=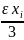
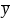 =
=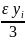 =
=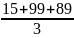 =68
=
=68
=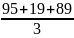 =68
=68
у
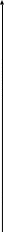
3д
2
1
3
2
2
10
20
30
40
50
60
70
80
90
40
50
60
70
80
90
100
110
30
20
10
х















3
3
3.
Целевая функция (показатель эффективности)
в задаче имеет вид:
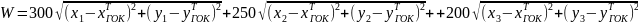
4. Рассчитать значение целевой функции в вершинах исходного симплекса.
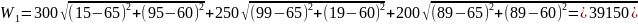
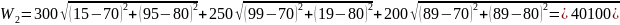
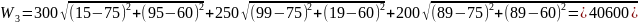
5. Суть метода — отражение вершины симплекса, к-рая имеет худшее значение целевой функции (т.е. наибольшее). Движение обратно — запрещено.
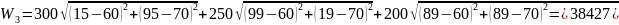
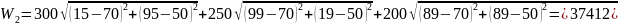

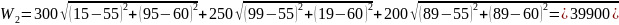
Симплекс замкнулся (зациклился). Из полученных значений выбираем наилучший, т.е. min: в данным случае это W2 = 37412 руб. Координаты (70; 50) являются искомыми координатами блока, а значит решением задачи.
