Задача 8
Умова: Значення факторної ознаки (х) та результативної (у) для 20 одиниць сукупності наведено в таблиці 15. Визначити:
1)наявність зв’язку між ознаками за допомогою методу аналітичного групування;
2)щільність зв’язку за допомогою лінійного коефіцієнта кореляції або кореляційного відношення залежно від форми зв’язку;
3)за результатами розрахунків зробити висновок.
Розв’язання
Таблиця 15 –Вихідні дані
варіант |
Кількість груп |
Ознака |
Значення ознаки |
|||||||||||||||||||
х |
181,6 |
180,6 |
181,2 |
182,8 |
182,1 |
181,4 |
183,2 |
180,7 |
183,7 |
181,6 |
183,8 |
182,6 |
180,3 |
183,1 |
182,2 |
181,5 |
180,7 |
182,8 |
181,3 |
182,8 |
||
78 |
7 |
у |
179 |
160 |
169 |
163 |
174 |
169 |
172 |
163 |
170 |
173 |
165 |
173 |
177 |
179 |
178 |
167 |
170 |
173 |
166 |
167 |
Аналітичні групування – це групування, які визначають взаємозв'язок між різними ознаками одиниць статистичної сукупності. За допомогою такого групування можна виявити певні взаємозв'язки між факторними і результативними ознаками. Аналітичні групування є дуже складними і для того, щоб зрозуміти, як вони будуються, необхідно чітко виділити факторні і результативні ознаки в досліджуваному явищі.
,
де: максимальне та мінімальне значення ознак одиниць сукупності.
Тепер розіб’ємо сукупність на 7 груп за факторною ознакою та розрахуємо середню величину результативної ознаки для визначення наявності зв’язку між ними:
Таблиця 16 - Розрахункові дані
Групи |
Кількість явищ з
результативною ознакою ( |
∑ у |
Середня величина
результативної ознаки ( |
180,3-180-8 |
4 |
670 |
167,50 |
180,8-181,3 |
1 |
169 |
169,00 |
181,3-181,8 |
5 |
854 |
170,80 |
181,8-182,3 |
2 |
352 |
176,00 |
182,3-182,8 |
1 |
173 |
173,00 |
182,8-183,3 |
5 |
854 |
170,80 |
183,3-183,8 |
2 |
335 |
167,50 |
Разом |
20 |
3407 |
856,30 |
)
За даною таблицею видно, що зі зростанням факторної ознаки, результативна спочатку спадає, потім зростає, а потім знову спадає і знову зростає. Побудуємо кореляційне поле, загальний вид якого вкаже характер зв’язку.
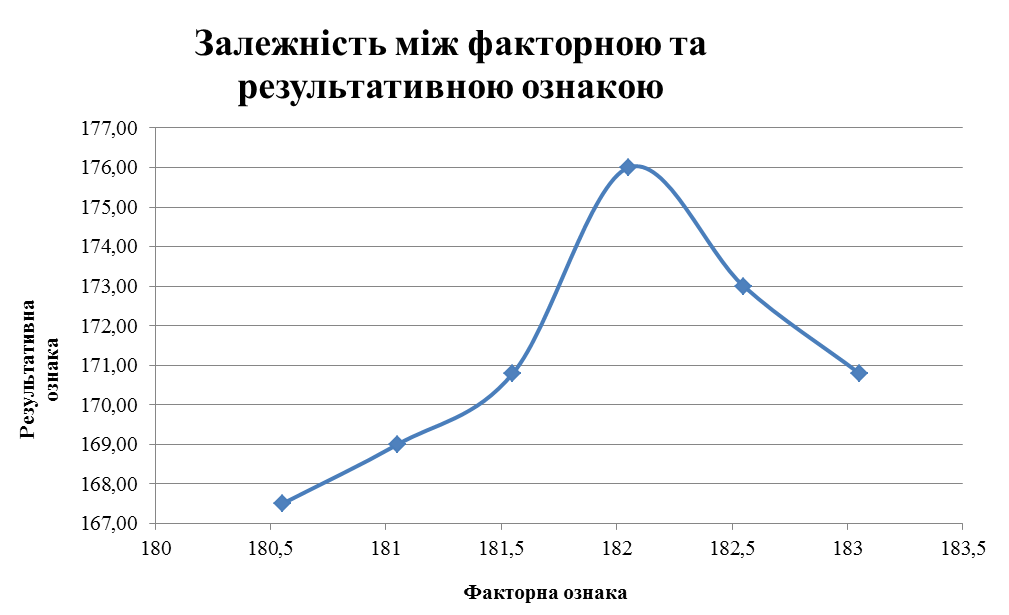
Рисунок 6 - Залежність між ознаками
По загальному розташуванню точок кореляційного поля, ми установили що форма нелінійна.
Так як у нас зв’язок нелінійний, щільність визначимо за допомогою універсального показника зв’язку – кореляційного відношення, за формулою:
,
(33.)
де
-
загальна дисперсія,знаходиться за
формулою
;
(34.)
-
міжгрупова дисперсія, знаходиться за
формулою
(35.);
(36.);
(37.).
Таблиця 17 – Розрахункові дані
Групи |
Кількість явищ з результативною ознакою ( |
∑ у |
Середня величина результативної ознаки ( ) |
|
|
|
180,3-180-8 |
4 |
670,00 |
167,50 |
-688,80 |
474445,44 |
1897781,76 |
180,8-181,3 |
1 |
169,00 |
169,00 |
-687,30 |
472381,29 |
472381,29 |
181,3-181,8 |
5 |
854,00 |
170,80 |
-685,50 |
469910,25 |
2349551,25 |
181,8-182,3 |
2 |
352,00 |
176,00 |
-680,30 |
462808,09 |
925616,18 |
182,3-182,8 |
1 |
173,00 |
173,00 |
-683,30 |
466898,89 |
466898,89 |
182,8-183,3 |
5 |
854,00 |
170,80 |
-685,50 |
469910,25 |
2349551,25 |
183,3-183,8 |
2 |
335,00 |
167,50 |
-688,80 |
474445,44 |
948890,88 |
Разом |
20 |
3407 |
856 |
|
|
6112229 |
Загальна
дисперсія:
.
Міжгрупова
дисперсія:
.
Отже,
.
Висновки:
За допомогою методу аналітичного
групування, ми визначила наявність
зв’язку між факторною та результативною
ознакою. Побудувавши кореляційне поле,
ми виявили, що даний зв’язок є нелінійним.
Кореляційне відношення, яке дорівнює
,
свідчить про нещільний зв'язок між
ознаками. Тобто результативна ознака
на 74% залежить від факторної ознаки, та
на 26% від інших факторів.