Практическое занятие №1.

Тема 1. Основные положения геометрической оптики.

Раздел 1.1. Основные законы отражения и преломления света. Принцип Ферма. Закон прямолинейного распространения света. Законы отражения и преломления света. Полное внутреннее отражение. Ход лучей в призме

Цель занятия: проработка вопросов, связанных с основными понятиями и законами геометрической оптики.

Студентам необходимо усвоить основные законы геометрической оптики, и используя их находить ход лучей при наличии преломляющих поверхностей, объясняя при этом важные оптические эффекты.

Задание: решение практических задач на нахождение бокового смещения световых лучей при прохождении через плоскопараллельную пластину, вычисление « кажущихся»: глубины, высоты и др. оптических эффектов, обусловленные преломлением света.

Список задач для решения в аудитории и для домашних заданий:

1. Луч света падает на плоскопараллельную пластинку толщиной d=6.0см. Угол падения . Найти величину бокового смещения луча, прошедшего через эту пластинку.

2. П ловец, нырнувший с открытыми глазами, рассматривает из-под воды светящуюся лампочку, находящуюся над его головой на расстоянии h=75см от поверхности воды. Каково будет кажущееся расстояние H от поверхности воды от лампочки? .

3. В стекле с показателем преломления имеется сферическая полость радиусом R=3см, заполненная водой ( ). На полость падают параллельные лучи света. Определить радиус светового пучка, который проникает в полость.

4. На краю бассейна стоит человек и наблюдает камень, лежащий на дне. Глубина бассейна h. На каком расстоянии от поверхности воды видно изображение камня, если луч зрения составляет с нормалью к поверхности воды угол i?

5. Луч света проходит через призму с преломляющим углом  и п.п. n. Пусть D – угол отклонения луча. Показать, что при симметричном ходе луча через призму:

6. а) угол D_min; б) .

Задачи для самостоятельного решения

1. Трехгранная призма с преломляющим углом 60⁰ дает угол наименьшего отклонения в воздухе 37⁰. Какой угол наименьшего отклонения дает эта призма в воде?

2. Предмет находится на расстоянии l=15см от плоскопараллельной стеклянной пластинки. Наблюдатель рассматривает предмет через пластинку, причем луч зрения нормален к ней. Определить расстояние x от изображения предмета до ближайшей к наблюдателю грани, если толщина пластинки d=4.5см, n=1.5 для стекла.

3. Показать, что при преломлении в призме с малым преломляющем углом , луч отклоняется на угол D(n-1)  независимо от угла падения, если последний также мал.

4. Луч света, содержащий две монохроматические составляющие, проходит через трехгранную призму с =80⁰. Определить угол между обеими составляющими луча после призмы, если показатели преломления для них равны 1,515 и 1,520. Призма ориентирована на угол наименьшего отклонения.

Практическое занятие №2.

Тема 1. Основные положения геометрической оптики.

Раздел 1.2. Элементы фотометрии. Основные фотометрические величины. Сила света. Световой поток. Освещенность. Светимость. Яркость.

Цель занятия: проработка вопросов, связанных с основными понятиями фотометрии.

Студентам необходимо усвоить такие понятия, как сила света, световой поток, поток энергии, освещенность, светимость, яркость; научиться использовать кривую спектральной чувствительности глаза для расчета фотометрических параметров оптических систем.

Задание на занятие: решение практических задач на нахождение силы света, светового потока, потока энергии, освещенности, светимости, яркости различных поверхностей.

Список задач для решения в аудитории и для домашних заданий:

1. Найти с помощью кривой относительной спектральной чувствительности глаза (рис.1)

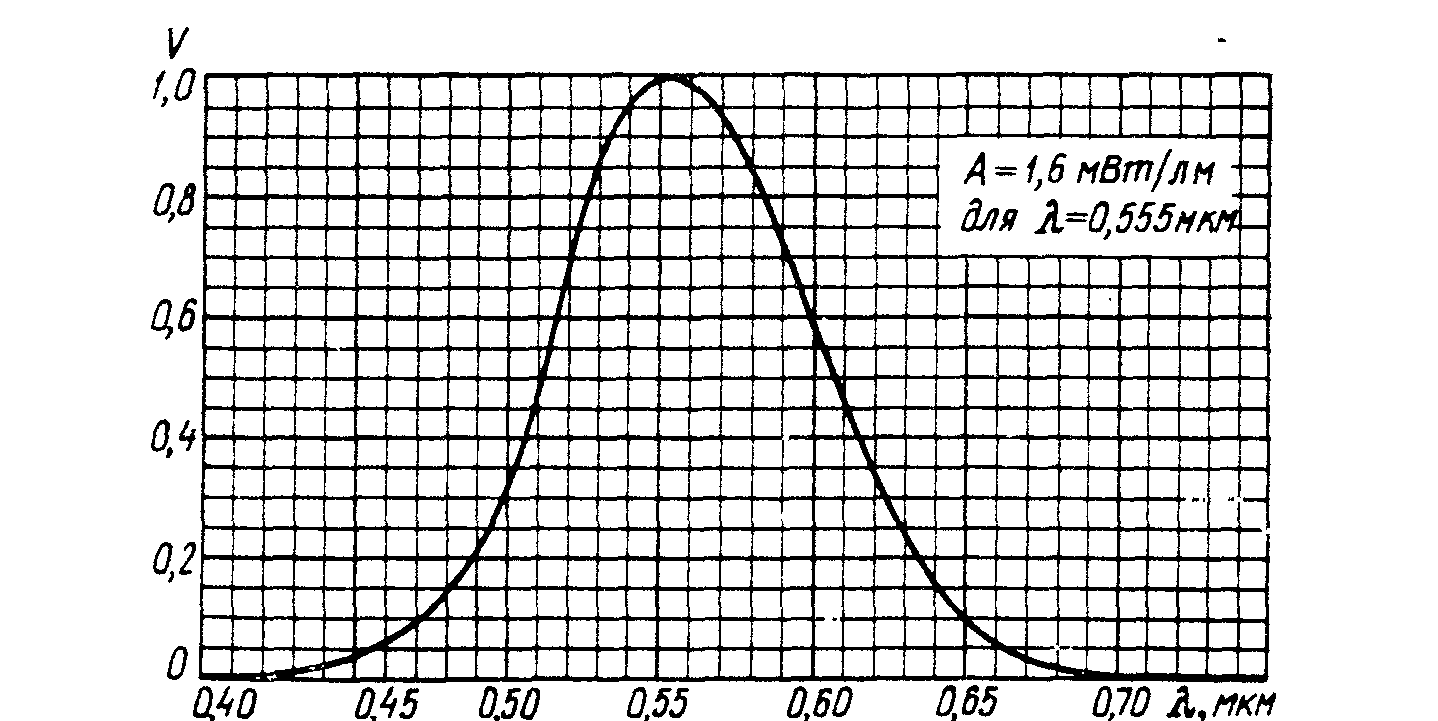
Рис.1. Кривая относительной спектральной чувствительности глаза

а) поток энергии соответствующий световому потоку 1 лм и длиной

волны 510нм и 640нм

б) световой поток, приходящийся на интервал длин волн от 580нм до 630нм, если соответствующий поток энергии равен 4,5 мВт, причем он распределен равномерно по всем длинам волн этого интервала. Считать, что в данном спектральном интервале функция спектральной чувствительности глаза линейна.

2. Найти среднюю освещенность облучаемой части непрозрачной сферы, если на нее падает:

а) параллельный световой поток, создающий в точке нормального падения освещенность E₀

б) свет от точечного изотропного источника, находящегося на расстоянии l=100см от центра сферы, r=60см и I=36кд.

3. Некоторая светящаяся поверхность подчиняется закону Ламберта. Ее яркость равна В. Найти:

а) световой поток, излучаемый элементом S этой поверхности внутрь конуса, ось которого нормальна к данному элементу, если угол полураствора конуса равен .

б) светимость такого источника.

4. На высоте h=1м над центром круглого стола радиусом r=1м подвешен точечный источник, кривая светораспределения которого I() обеспечивает равномерную освещенность всех точек стола (I – сила света,  - угол между лучом и вертикалью). Найти вид функции I() и световой поток, падающий на стол, если I(0)=I₀=100кд.

Задачи для самостоятельного решения

1. Вертикальный луч прожектора освещает центр потолка круглой темной комнаты радиусом r = 2,0 м. При этом на потолке образуется зайчик площадью S = 100см². Освещенность зайчика Е =1000 лк. Коэффициент отражения потолка  = 0,80. Найти наибольшую освещенность стены, создаваемую светом, отраженным от потолка. Считать, что отражение происходит по закону Ламберта.

2. Светильник, имеющий вид равномерно светящейся сферы радиусом r₀=6,0см, находится на расстоянии h=3,0м от пола. Яркость светильника B=2,0·10⁴кд/м² и не зависти от направления. Найти освещенность пола непосредственно под светильником.

3. Равномерно светящийся купол, имеющий вид полусферы, опирается на горизонтальную поверхность. Определить освещенность в центре этой поверхности, если яркость купола равна В и не зависти от направления.

Практическое занятие №3