2.8.2 Рассчитываем вал колеса по следующим пунктам:

а) Определяем размеры первой ступени вала под элемент открытой передачи:

d₁ = 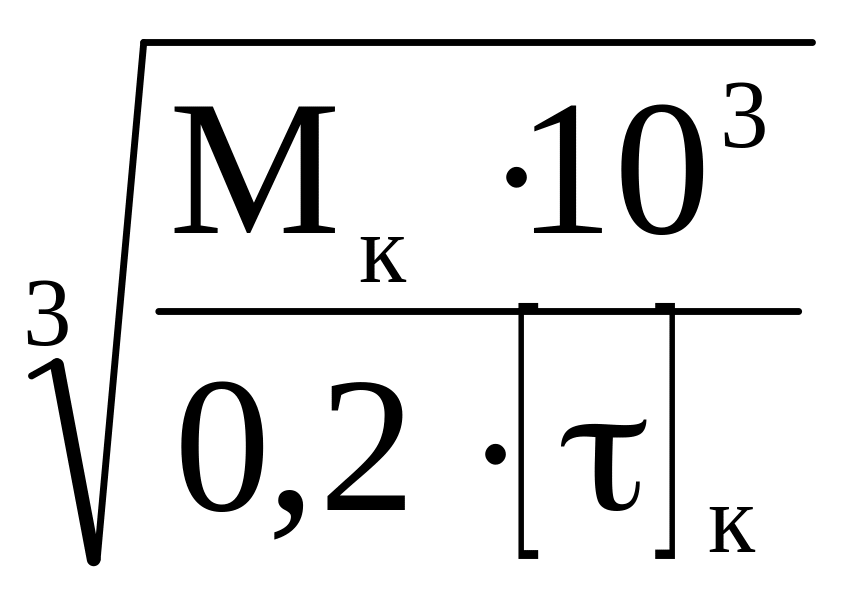, (96)

где M_k=Т – крутящий момент, равный вращающему моменту на валу, Н∙м,

d₁= =42 мм,

l₁ = 1,5d₁, (97)

l₁ = 1,2*42=50 мм.

б) Определяем размеры второй ступени вала под уплотнение крышки с отверстием и подшипник:

d₂ = d₁ + 2t, (98)

где t- высота буртика, t =2,5 мм,

d₂ =42+2*1,5=45 мм.

Под подшипник выбираем d₂ =45 мм.

l₂ = 2d₂, (99)

l₂ = 1,25*45=56 мм.

в) Определяем размеры третьей ступени вала под колесо:

d₃= d₂+3,2r, (100)

где r – координата фаски подшипника, r =2,5 мм

d₃=45+3,2*2=50 мм,

l₃ определяется графически на эскизной компоновке.

г) Определяем размеры четвертой ступени вала под подшипник:

d₄ = d₂, (101)

d₄ =45 мм,

l₄ =В+с, (102)

l₄ =17+2=19 мм.

2.9 Расчетная схема валов редуктора

2.9.1 Построим эпюру изгибающих и крутящих моментов быстроходного вала

Исходные данные:

Окружная сила, действующая в зацеплении F_t1, Н 1579,10

Радиальная сила, действующая в зацеплении F_r1, Н 574,21

Осевая сила, действующая в зацеплении F_а1, Н 221,92

Консольная сила от открытой передачи F_оп, Н 1303,68

Диаметр окружности вершин шестерни d_а1, мм 54,49

Рисунок 2 – Эпюры изгибающих моментов.

а) Рассматриваем горизонтальную плоскость. Определяем опорные реакции, Н:

F_a*r-F_r*0,051+R_yd*0.102-F_оп*0,177

R_yd=

R_yd=640,49Н

F_a*r-F_оп*0,075+F_r*0,051-R_yc*0,102

R_yc*0,102=221,928*0,025245-1303,68*0,075+574,218*0,051

R_yc=319,29Н

Проверка:

-R_yc-F_r+ R_yd-F_оп =0

-616,552-574,218+2494,45-1303,68=0

б) Построим эпюру изгибающих моментов относительно оси Y в характерных сечениях, Н∙м:

;

;

=-319,29*0,0058=-18,518 Н*м

;

=-R_yc*0,102-F_a1*r-F_r1*0,058

Н*м;

=-R_yc*0,177-F_a*r-F_r1*0,126+R_yd*0,075

в) Рассматриваем вертикальную плоскость. Определяем опорные реакции, Н:

,

=

R_xc*0,102-F_t1*0,051=0,

R_xc= ,

Проверка:

-R_xc+F_t1-R_xd=0

-789,55+1579,1-3990-789,55=0

г) Построим эпюру изгибающих моментов относительно оси X в характерных сечениях, Н∙м:

;

- R_xc *0,051,

=103,443 Н*м;

103,443;

-R_xc*0,102+F_t1*0,051

=-80,534+80,534=0.

д) Построим эпюру крутящих моментов:

М_к=(F_t1*d₁)/2,

М_к= =294,231 Н*м.

е) Определяем суммарные радиальные реакции R_A и R_B, Н, по формулам:

R_A= (103)

R_A= Н,

R_B= , (104)

R_B= Н

ж) Определяем суммарные изгибающие моменты в наиболее нагруженных сечениях, Н∙м:

ΣМ₂= , (105)

ΣМ₂= ,

ΣМ₃= ,