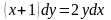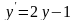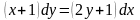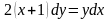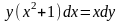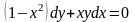- •Введение
- •1. Организация и порядок проведения практических занятий
- •Критерии оценки
- •Практическая работа № 1
- •Теоретические сведения
- •Раскрытие неопределенностей вида :
- •Раскрытие неопределенностей вида :
- •Индивидуальные задания
- •Практическая работа № 2
- •Теоретические сведения
- •Индивидуальные задания
- •Практическая работа № 3
- •Теоретические сведения
- •Индивидуальные задания
- •Практическая работа № 4
- •Теоретические сведения
- •Индивидуальные задания
- •Практическая работа № 5.
- •Теоретические сведения
- •И ндивидуальные задания. Практическая работа № 6
- •Теоретические сведения
- •Индивидуальные задания
- •Проверьте себя:
- •Практическая работа № 7
- •Теоретическая справка
- •Индивидуальные задания
Индивидуальные задания
Проверьте себя:
№ |
Примеры |
Ответы |
1. |
|
|
2. |
|
|
3. |
|
|
Задание№1. Проверить, является ли функция решением дифференциального уравнения.
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
Задание№2. Найти частное решение.
1 |
|
2 |
|
3 |
xdx = dy (1;0) |
4 |
xdx=ydy (2;1) |
5 |
|
6 |
|
7 |
|
8 |
|
Задание №3. Найти общее решение.
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
Практическая работа № 7
Тема работы: Решение дифференциальных уравнений второго порядка с постоянными коэффициентами.
Теоретическая справка
Если коэффициенты при у, yи y– постоянные, то уравнение ypyqy 0, где p и q – вещественные числа, называется линейным однородным дифференциальным уравнением 2-го порядка с постоянными коэффициентами.
Общее решение уравнения имеет вид: y0 C y1 C y2 , где у1 и у2 – два линейно независимых частных решения этого уравнения, С1 и С2 – произвольные постоянные.
Для нахождения линейно независимых частных решений у1 и у2 уравнения используется квадратное уравнение вида
k2 pk q 0 , которое называется характеристическим уравнением для уравнения.
В таблице 1 приведены виды функций у1 и у2 и вид общего решения равнения в зависимости от вида корней характеристического уравнения.
Таблица 1.
Корни характеристического уравнения
|
Вид функций у1 и у2 |
Вид общего решения уравнения
|
Вещественные различные k1 k2
|
y1=ek1x y2=ek2x
|
y0=C1 ek1x+C2 ek2x |
Вещественные равные k1 k2 k
|
y1 ekx, y2 =xekx
|
y0=C1 ekx+C2 xekx |
Комплексно- сопряженные k1,2 i
|
y1 =e xcos( x), y2 e xsin(x
|
y= e x(C1 cos( x)+C2 sin(x |
Пример 1. Найти общее решение уравнения y16y 0.
Решение. Характеристическое уравнение для данного однородного уравнения имеет вид k2 16 0 (коэффициент при yравен нулю). Его корнями являются комплексные числа k1 4i, k2 4i. Здесь 0, 4. Тогда общее решение данного уравнения: y C1 cos(4x) C2 sin(4x).


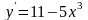 (-1;1)
(-1;1)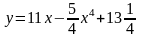
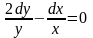
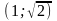
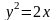
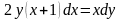
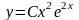
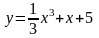
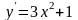
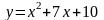
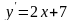
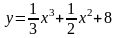
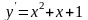
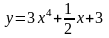
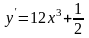
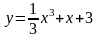
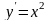
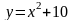
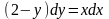 (1;2)
(1;2)
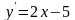
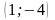
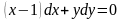 (2;0)
(2;0)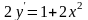 (0;0)
(0;0)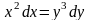 (-1;1)
(-1;1)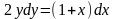 (1;4)
(1;4)