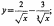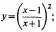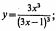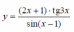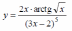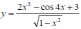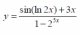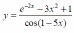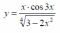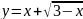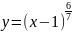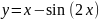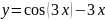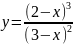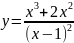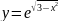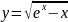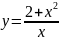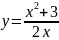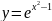Индивидуальные задания
Найдите производные функций и, при необходимости, вычислите их значения:
Вариант 1 |
Вариант 2 |
Вычислите
|
В
ычислите
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
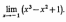
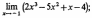
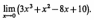
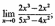
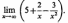
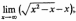
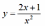
Практическая работа № 3
Тема работы: Условия монотонности функции. Необходимое и достаточное условие экстремума
Теоретические сведения
Для определения промежутков монотонности функции y = f(x) используют достаточный признак монотонности.
Достаточный признак монотонности дифференцируемой функции:
Если на интервале х(а, b) производная f ‘(x) сохраняет знак, то функция y = f (x) сохраняет монотонность на этом интервале, а именно: если f ‘(x) > 0, то f(x) возрастает, если f ‘(x) <0 , то f(x) убывает.
Для установления точек экстремумов функции y = f (x) используют необходимый и достаточные признаки существования экстремума.
Необходимое условие существования экстремума функции: если непрерывная функция y = f (x) имеет экстремум в точке х0, то ее производная в этой точке равна нулю или не существует.
Точки, принадлежащие ООФ, в которых производная f ‘(x) равна нулю или не существует, называют критическими точками функции по ее первой производной (точками, «подозрительными на экстремум»).
Первый достаточный признак существования экстремума: если при переходе через критическую точку х0 (слева направо) производная f ‘(x) изменяет свой знак, то в точке х0 есть экстремум причем это максимум, если знак f ‘(x) меняется с плюса на минус, и это минимум, если знак f ‘(x) меняется с минуса на плюс. Если при переходе через критическую точку х0 производная f ‘(x) не изменяет свой знак, то в точке х0 нет экстремума функции f (x) .
Второй достаточный признак существования экстремума: если y = f (x) – дважды дифференцируемая функция в точке х0 и f ‘(x0)=0, тогда: если f ‘’(x0 ) < 0, то х0 – точка минимума функции, а если f ‘’(x0 ) > 0, то х0 – точка максимума.
Для нахождения точек экстремумов функции y = f (x) сначала находят критические точки по первой производной. После этого проверяют выполнение в них достаточных условий существования экстремума функции.
Индивидуальные задания
Найти промежутки возрастания и убывания функции. Найти точки экстремума
Вариант 1
|
Вариант 2
|
|
|
|
|
|
|
|
|
|
|
|
|
