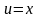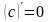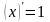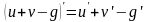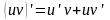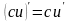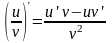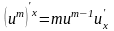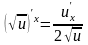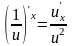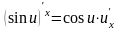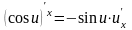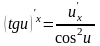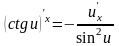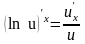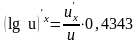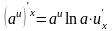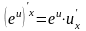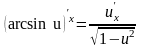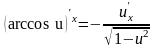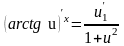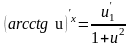- •Введение
- •1. Организация и порядок проведения практических занятий
- •Критерии оценки
- •Практическая работа № 1
- •Теоретические сведения
- •Раскрытие неопределенностей вида :
- •Раскрытие неопределенностей вида :
- •Индивидуальные задания
- •Практическая работа № 2
- •Теоретические сведения
- •Индивидуальные задания
- •Практическая работа № 3
- •Теоретические сведения
- •Индивидуальные задания
- •Практическая работа № 4
- •Теоретические сведения
- •Индивидуальные задания
- •Практическая работа № 5.
- •Теоретические сведения
- •И ндивидуальные задания. Практическая работа № 6
- •Теоретические сведения
- •Индивидуальные задания
- •Проверьте себя:
- •Практическая работа № 7
- •Теоретическая справка
- •Индивидуальные задания
Практическая работа № 1
Тема работы: предел функции
Теоретические сведения
Раскрытие неопределенностей вида :
Пусть f(x) – рациональная дробь. Числитель и знаменатель дроби раскладывают на множители.
П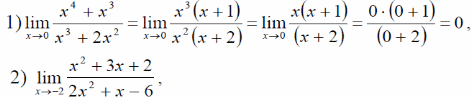 ример:
ример:
Разложим квадратный трехчлен на множители, решив квадратное уравнение
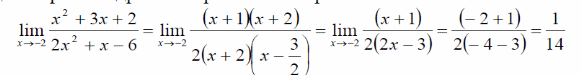
Пусть f(x) – дробь, содержащая иррациональные выражения. Тогда применим правило «избавления от иррациональности» путем умножения соответствующих частей дроби на число, сопряженное иррациональной части, или правило замены переменной.
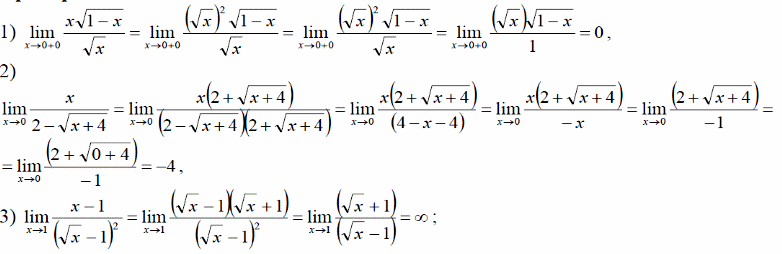
П
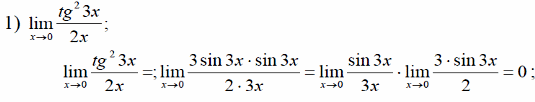 усть
f(x)
– дробь, содержащая тригонометрические
функции. Для раскрытия неопределенностей,
в этом случае, используется первый
замечательный предел или эквивалентные
бесконечно малые функции.
усть
f(x)
– дробь, содержащая тригонометрические
функции. Для раскрытия неопределенностей,
в этом случае, используется первый
замечательный предел или эквивалентные
бесконечно малые функции.
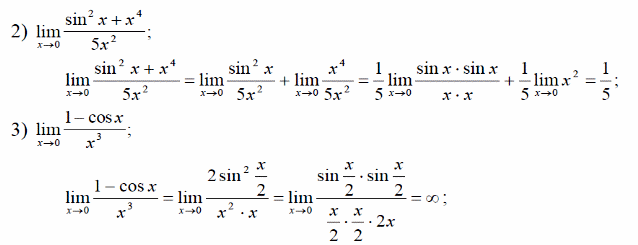
Раскрытие неопределенностей вида :
Пусть f(x) – рациональная дробь. Тогда делим и числитель и знаменатель на переменную в старшей степени.
П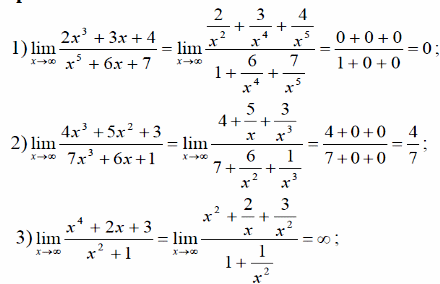 римеры
римеры
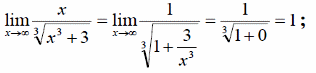
Индивидуальные задания
Вычислить пределы
Вариант 1 |
Вариант 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Практическая работа № 2
Тема работы: Производная функции
Теоретические сведения
Производной функции y=f(x) называется предел отношения приращения функции y к приращению аргумента x, когда x стремится к нулю:
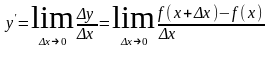
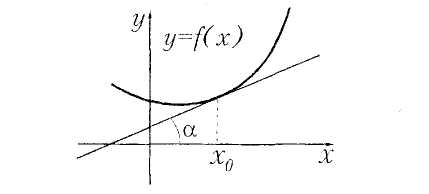
Геометрический смысл производной:
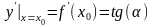
- тангенс угла наклона касательной к графику функции y=f(x) в точке с абсциссой x0
Физический смысл
производной: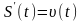 -
скорость движения тела в момент времени
t
при прохождении пути S(t).
-
скорость движения тела в момент времени
t
при прохождении пути S(t).
Функция, имеющая производную, называется дифференцируемой. Операция нахождения производной называется дифференцированием.
Таблица производных
Таблица формул дифференцирования
|
При условии
|
При условии
|
I |
|
|
II |
|
|
III |
|
|
IV |
|
|
V |
|
|
VI |
|
|
VII |
|
|
VIII |
|
|
IX |
|
|
X |
|
|
XI |
|
|
XII |
|
|
XIII |
|
|
XIV |
|
|
XV |
|
|
XVI |
|
|
XVII |
|
|
XVIII |
|
|
XIX |
|
|
XX |
|
|
XXI |
|
|
Правила дифференцирования
Производная постоянной С равна нулю:
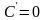
Производная суммы двух функций равна сумме производных этих функций:
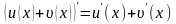
Производная произведения двух функций:
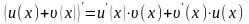
В частности,
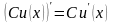
Производная частного двух функций:
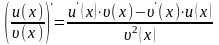
Производная сложной функции: если
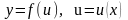 ,
,
то
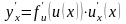 ,
,
то есть производная сложной функции по независимой переменной x равна произведению производной этой функции по промежуточной переменной u на производную промежуточной переменной по независимой переменной x.

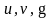 -
функция х
-
функция х