
- •§0. Элементы комбинаторики
- •§ 1. Классическое определение вероятности
- •§2. Вероятности суммы и произведения событий
- •§ 3. Формула полной вероятности и формула байеса
- •§4. Повторные независимые испытания
- •§5. Геометрические вероятности
- •§6. Дискретная случайная величина
- •§7. Непрерывная случайная величина
- •§8. Нормальный закон
§7. Непрерывная случайная величина
7.1.
Случайная величина
задана на всей оси
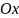 функцией распределения
функцией распределения
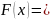 1/2 + (arctgx)/π. Найти вероятность того, что
в результате испытания величина
примет значение, заключенное в интервале
(0,1).
1/2 + (arctgx)/π. Найти вероятность того, что
в результате испытания величина
примет значение, заключенное в интервале
(0,1).
7.2.
Функция распределения случайной величины
(времени безотказной работы некоторого
устройства) равна
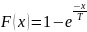 ,
,
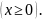 Найти вероятность безотказной работы
устройства за время
Найти вероятность безотказной работы
устройства за время
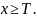
7.3. Случайная величина задана функцией распределения
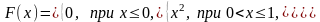 Найти
вероятность того, что в результате
четырех независимых испытаний величина
ровно три раза примет значение,
принадлежащее интервалу (0,25, 0,75).
Найти
вероятность того, что в результате
четырех независимых испытаний величина
ровно три раза примет значение,
принадлежащее интервалу (0,25, 0,75).
7.4. Дана функций распределения случайной величины :
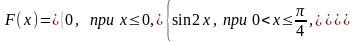 Найти
плотность распределения
Найти
плотность распределения
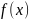 и
и
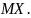
7.5.
Случайная величина
в интервале (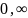 ) задана плотностью распределения
) задана плотностью распределения
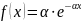 (α
> 0); вне этого интервала
(α
> 0); вне этого интервала
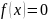 .
Найти вероятность того, что
примет значение, принадлежащее интервалу
(1,2).
.
Найти вероятность того, что
примет значение, принадлежащее интервалу
(1,2).
7.6.
Плотность распределения случайной
величины
в интервале ( − π/2,π/2) равна
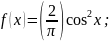 вне
этого интервала
.
Найти вероятность того, что в трех
независимых испытаниях
примет ровно два раза значение,
принадлежащее интервалу (0,π/4).
вне
этого интервала
.
Найти вероятность того, что в трех
независимых испытаниях
примет ровно два раза значение,
принадлежащее интервалу (0,π/4).
7.7. Задана плотность распределения случайной величины :
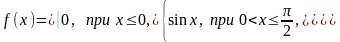
Найти
функцию распределения
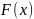 .
.
7.8.
Плотность распределения случайной
величины
задана на всей оси
равенством
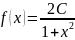 .
Найти постоянный параметр C.
.
Найти постоянный параметр C.
7.9.
Плотность распределения случайной
величины
X в интервале (0,π/2) равна
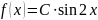 ;
вне этого интервала
.
Найти постоянный параметр
.
;
вне этого интервала
.
Найти постоянный параметр
.
7.10.
Случайная величина X задана плотностью
распределения
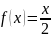 в интервале (0;2); вне этого интервала
= 0. Найти математическое ожидание
величины
.
в интервале (0;2); вне этого интервала
= 0. Найти математическое ожидание
величины
.
7.11.
Случайная величина
задана плотностью распределения
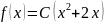 в интервале (0;1); вне этого интервала
= 0. Найти: а) параметр C; б) математическое
ожидание величины
.
в интервале (0;1); вне этого интервала
= 0. Найти: а) параметр C; б) математическое
ожидание величины
.
7.12..
Случайная величина
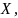 возможные
значения которой неотрицательны, задана
функцией распределения
возможные
значения которой неотрицательны, задана
функцией распределения
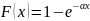 (α
> 0). Найти математическое ожидание
величины
.
(α
> 0). Найти математическое ожидание
величины
.
7.13.
Случайная величина
задана плотностью распределения
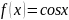 в
интервале (0,π/2); вне этого интервала
в
интервале (0,π/2); вне этого интервала
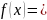 0. Найти математическое ожидание и
дисперсию случайной величины
0. Найти математическое ожидание и
дисперсию случайной величины
7.14. Случайная величина задана плотностью распределения
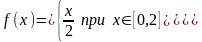 Найти
функцию распределения и вероятность
того, что
Найти
функцию распределения и вероятность
того, что
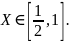
7.15.
Случайная величина
в интервале (2,4) задана плотностью
распределения
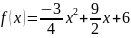 ;
вне этого интервала
=
0. Найти математическое ожидание и
дисперсию величины
.
;
вне этого интервала
=
0. Найти математическое ожидание и
дисперсию величины
.
7.16.
Случайная величина
в интервале (0,π) задана плотностью
распределения
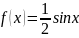 ;
вне этого интервала
;
вне этого интервала
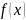 = 0. Найти математическое ожидание и
дисперсию
.
= 0. Найти математическое ожидание и
дисперсию
.
7.17.
Случайная величина
в интервале (0,5) задана плотностью
распределения
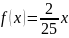 ;
вне этого интервала f(x)
= 0. Найти математическое ожидание и
дисперсию
.
;
вне этого интервала f(x)
= 0. Найти математическое ожидание и
дисперсию
.
7.18. Случайная величина имеет плотность распределения
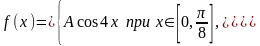 Найти
коэффициент
и функцию распределения. Построить
графики плотности распределения и
функции распределения.
Найти
коэффициент
и функцию распределения. Построить
графики плотности распределения и
функции распределения.
7.19. Случайная величина задана плотностью распределения
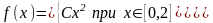 Найти:
а) постоянную
Найти:
а) постоянную
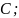 б) функцию распределения
б) функцию распределения
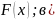 вероятности
вероятности

7.20.
Задана функция распределения случайной
величины
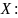
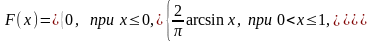
Найти
плотность распределении данной случайной
величины и вероятность того, что
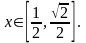
7.21. Годовой доход случайно выбранного налогоплательщика описывается случайной величиной с плотностью распределения
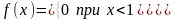 Найти
значение параметра
Найти
значение параметра
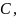 средний годовой доход и среднее
квадратичное отклонение годового
дохода.
средний годовой доход и среднее
квадратичное отклонение годового
дохода.
