Тема 6. Численное дифференцирование. Решение обыкновенных дифференциальных уравнений.

Задание 1:

Функция f(x) определена на отрезке [1:1.2] (см. таблицу 1). Выбрав шаг h=0.05, найти приближенные значения производных f (x) , f(x) в точках 1 и 1.10; оценить погрешность вычислений. Сравнить результаты с точными значениями производных в этих точках.

Задание 2:

Найти решение задачи Коши для дифференциального уравнения первого порядка на равномерной сетке отрезка [a,b] один раз с шагом h=0,2, другой - с шагом 0,1 методами Эйлера, Эйлера - Коши и классическим методом Рунге - Кутта. Сравнить численное решение с точным. Результаты представить в виде таблиц.

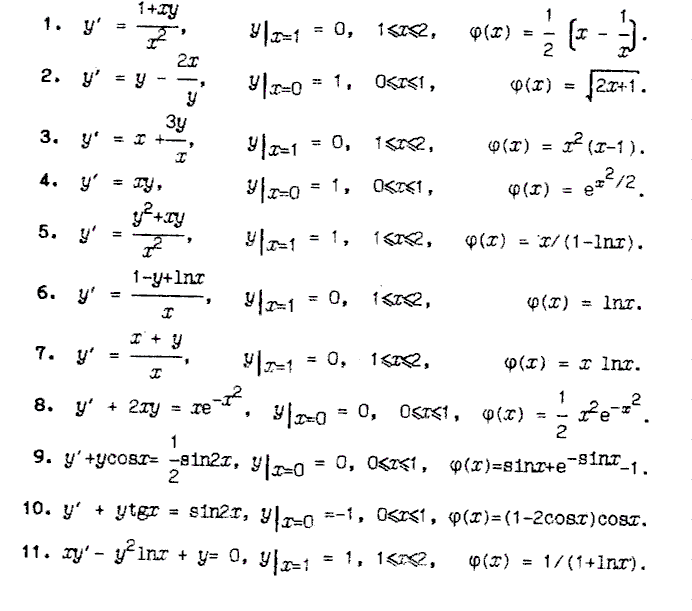
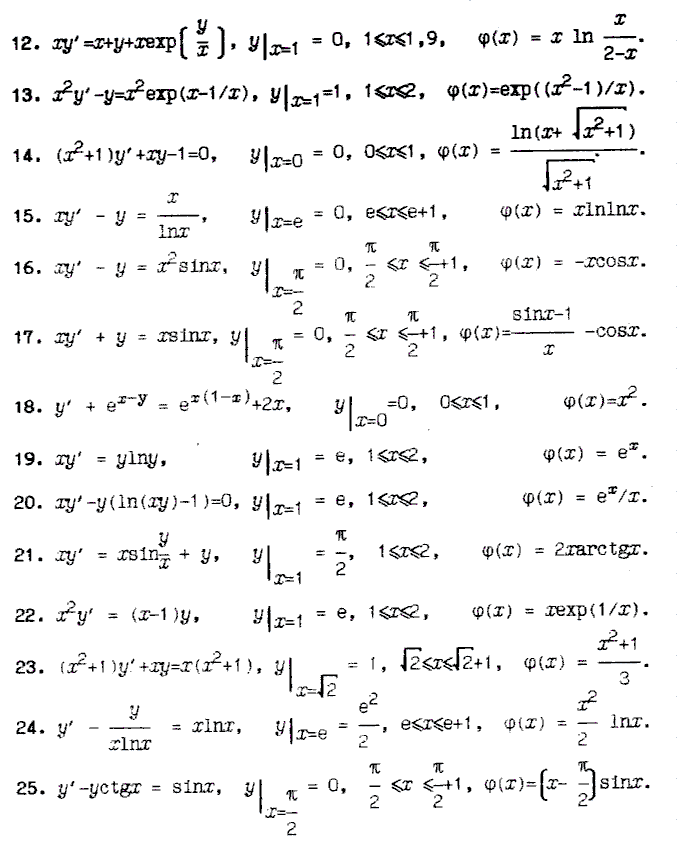
Задание 3:

З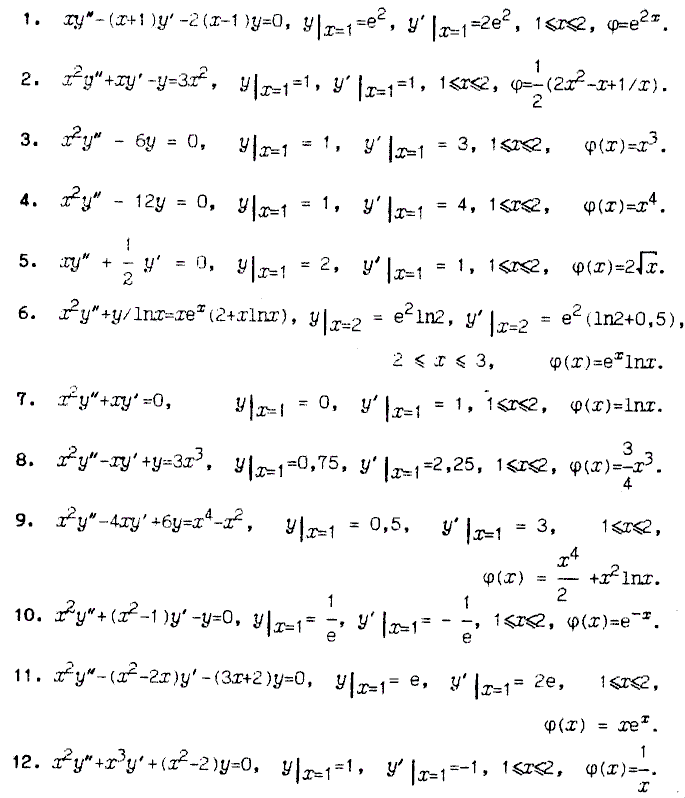 адачу Коши для дифференциального уравнения второго порядка преобразовать к задаче Коши для системы дифференциальных уравнений первого порядка. Найти решение последней задачи методом Рунге – Кутта на сетке отрезка [a, b]. Вычисления провести дважды с шагами h и h/2, полагая h=0,2. Найти численное решение дифференциального уравнения и оценить его погрешность. Сравнить численное решение с известным аналитическим решением. Результаты представить в виде таблицы.

Т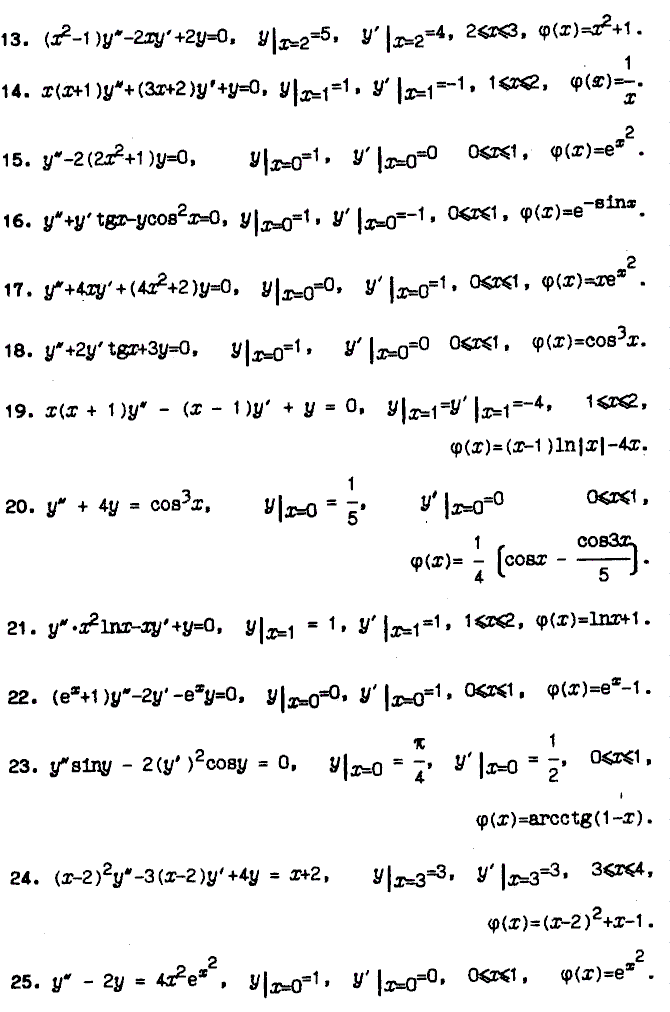 ема 8: Решение дифференциальных уравнений в частных производных

Задание: Составить программы с использованием метода конечных разностей решения уравнений: одномерного и двумерного теплопроводности, одномерного и двумерного уравнения Лапласа, одномерного и двумерного уравнения Пуасона, двумерного волнового уравнения. Постановку физической задачи, соотвествующую вышеперечисленным уравнениям произвести самостоятельно.

Тема 9: Интегральные уравнения

Задание:

Численно решить одномерное линейное интегральное уравнение 2 – рода для случаев:

Номер варианта	Ядро ИУ	Правая часть	
1	1	x	[1,2]
2	(x-S)	2x	[1,2]
3	2-(x-S)	x2	[1,2]
4	-2+3(x-s)	x	[1,2]
5	exp(x-S)	1	[0,1]
6	exp(-(x-s)	2	[0,1]
7	2(x-s)	x	[1,2]
8	2x	x2	[1,2]
9	sin(x-s)	1	[0,/2]
10	2cos(x-s)	1	[0,/2]

Список литературы

1. Бабенко К.И. Основы численного анализа. - М.:Наука,1986.-744с.

2. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. -М.:Наука,1987.

3. Боглаев Ю.П. Вычислительная математика и программирование: Учеб. пособие для студентов втузов.-М.:Высшая школа,1990.-544с.

4. Турчак Л.И. Основы численных методов: Учеб. пособие.-М.: Наука, 1987.-320с.

5. Волков Е.А. Численные методы.-М.:Наука,1982.-220с.

6. Самарский А.А. Теория разностных схем.-М.:Наука,1982.-540с.

7. Мак-Кракен Д., Дорн У. Численные методы и программирование на фортране.-М.:Мир,1977.-584с.

8. Ракитин В.И., Первушин В.Е. Практическое руководство по методам вычислений с приложением программ для персональных компьютеров: Учеб.пособие.-М.-:Высшая школа., 1998.-383с.

9. Волков Е.А. Численные методы.- М.:Наука,1987.-178с.

10. Мудров А.Е. Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль.-Томск: МП ”РАСКО “,1991.-272с.

11. Гулд Х., Тобочник Я. Компьютерное моделирование в физике, в 2 томах.-М.:Мир,1990.

12. Бурсиан Э.В. Задачи по физике для компьютера: Учеб.пособие.-М.:Просвещение,1991.-256с.