
- •«Численные методы в радиофизике»
- •0702 «Прикладная физика»
- •Тема 1. Численное интегрирование
- •Тема 2. Численное решение систем линейных алгебраических уравнений
- •Тема 3: Решение нелинейных уравнений
- •Тема 4. Решение систем нелинейных уравнений
- •Тема 5. Аппроксимация функций
- •Тема 6. Численное дифференцирование. Решение обыкновенных дифференциальных уравнений.
- •Тема 9: Интегральные уравнения
- •Задания
- •Специальности 6.070200 «Радиофизика и электроника»
- •0702 «Прикладная физика»
- •Редактор н.А.Василенко
- •95007, Г. Симферополь, ул. Ялтинская, 4
Министерство образования и науки Украины
Таврический национальный университет им. В.И. Вернадского
кафедра радиофизики
Задания
к практикуму по курсу
«Численные методы в радиофизике»
(раздел 1 «Численные методы»)
для студентов 3 курса дневной формы обучения
специальности 6.070200 «радиофизика и электроника»
образовательно - квалификационного уровня «бакалавр»
профессионального направления подготовки
0702 «Прикладная физика»
Симферополь 2002
Печатается по решению научно-методического совета ТНУ
от 15.05.01
Численные методы в радиофизике - курс базового цикла профессионально – ориентированных дисциплин, обязательный для изучения всеми студентами специальностей «Радиофизика и электроника». Читается в течение одного семестра на третьем курсе.
Предметом изучения дисциплины «Численные методы в радиофизике» являются численные методы и применение их для решения радиофизических задач.
Первый раздел курса содержит описание базовых численных методов. Его целью является изучение основных идей методов их особенностей и возможностей применения в прикладных исследованиях.
Предлагаемое пособие включает в себя задания к практическим занятиям по данному курсу.
Тема 1. Численное интегрирование
Задание:
Вычислить заданные интегралы по формулам прямоугольников, трапеций и Симпсона, если отрезок интегрирования разбит на n=2 и n=4 равные части. Оценить погрешность результата и сравнить приближенные значения интеграла с точными.

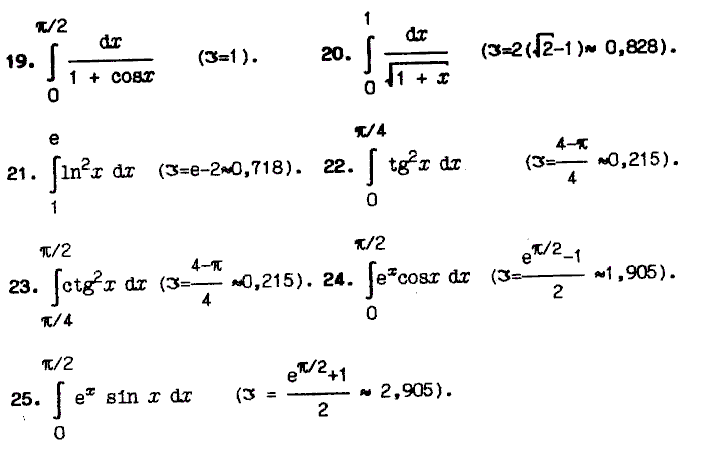
Тема 2. Численное решение систем линейных алгебраических уравнений
Задание:
Найти решения систем линейных алгебраических уравнений Ax=b методом Гаусса и методом итераций с точностью =10-2



 1.
6.
1.
6.


2
 . 7.
. 7.
3

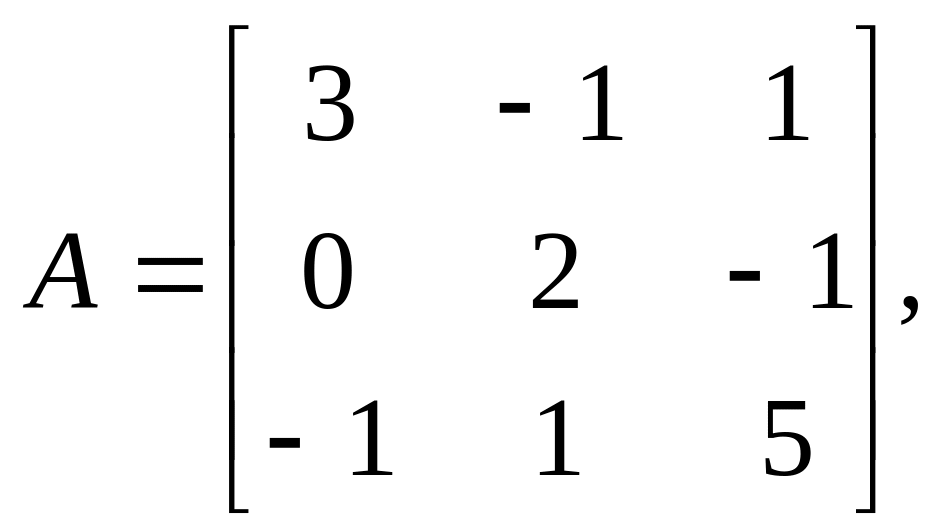
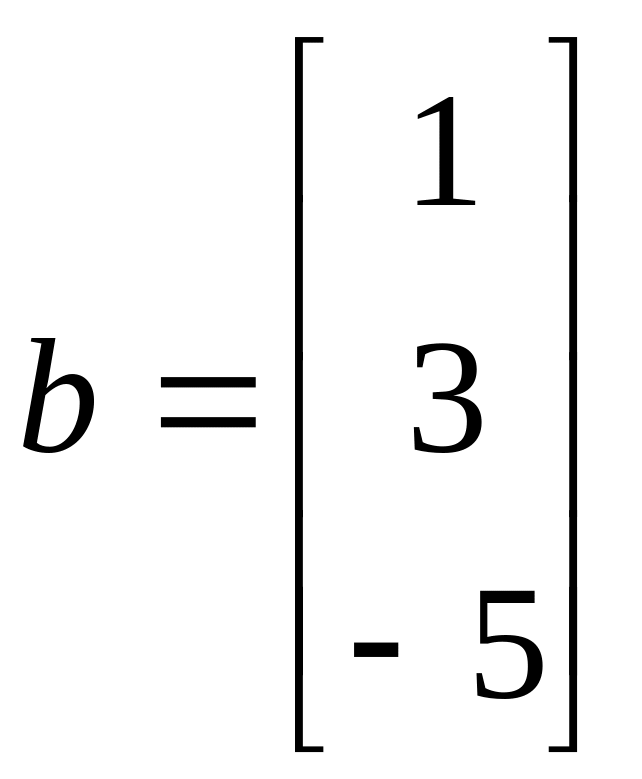 . 8.
. 8.
4


 . 9.
. 9.
5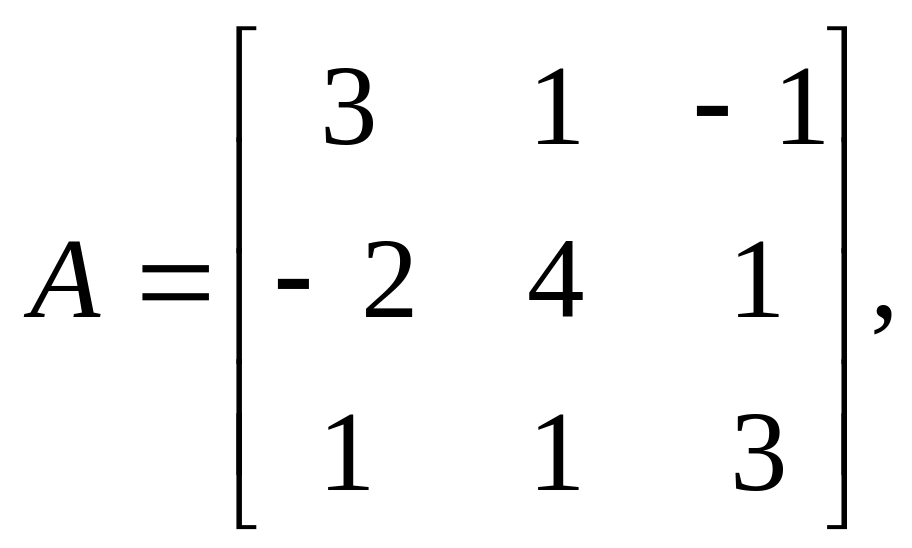

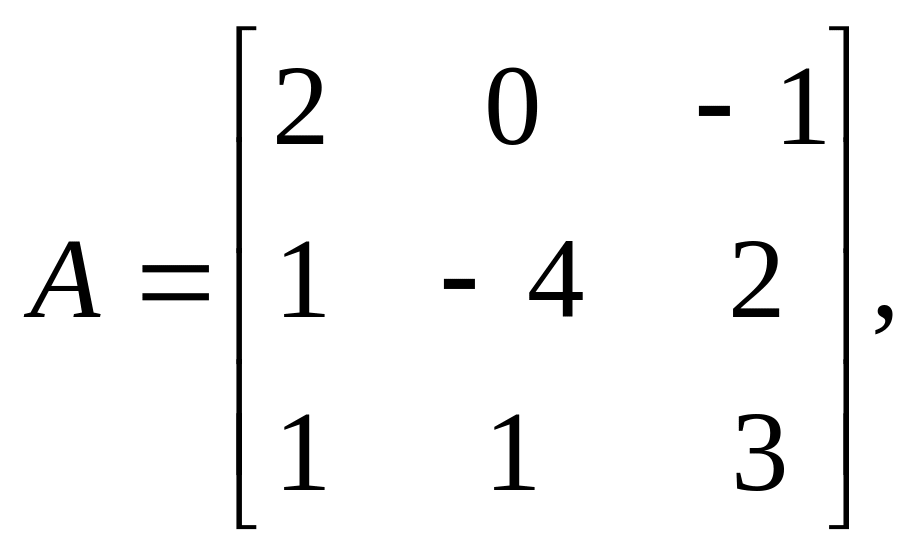
 . 10.
. 10.
1


 1. 19.
1. 19.


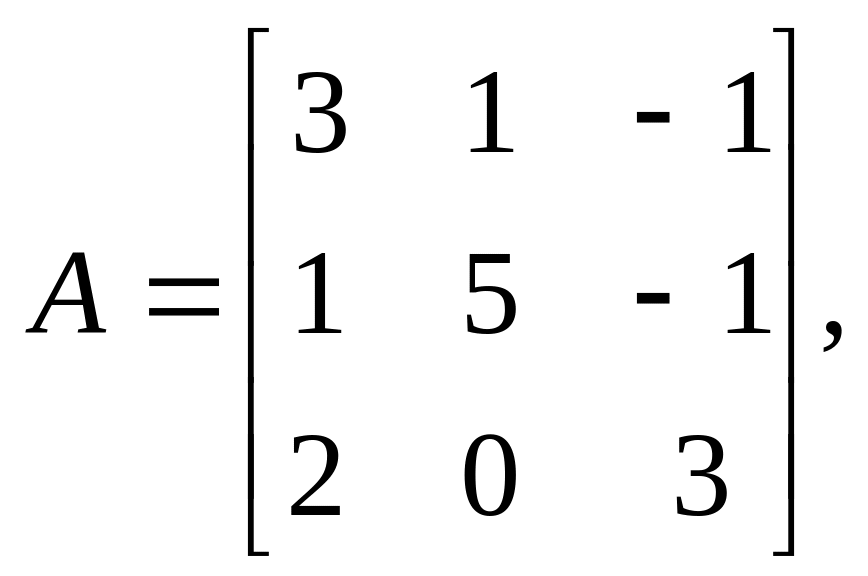

12. 20.


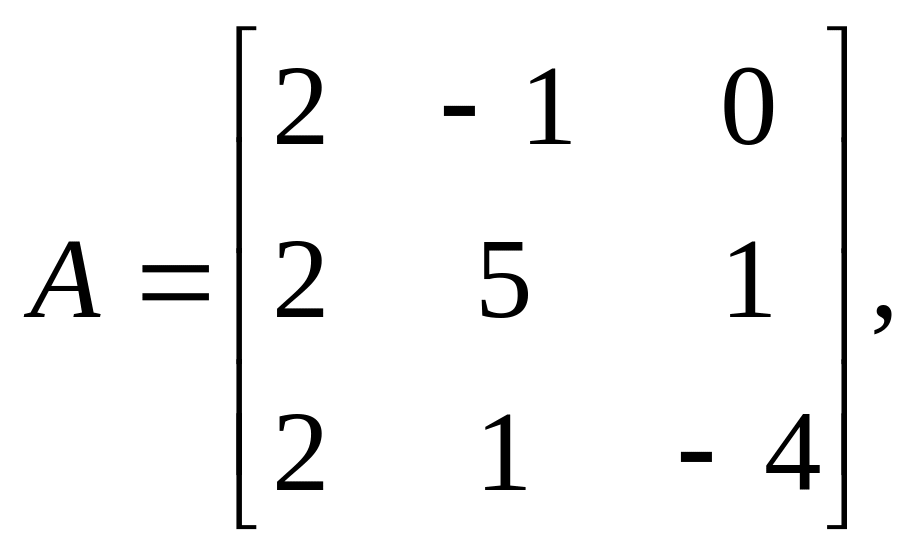

13. 21.
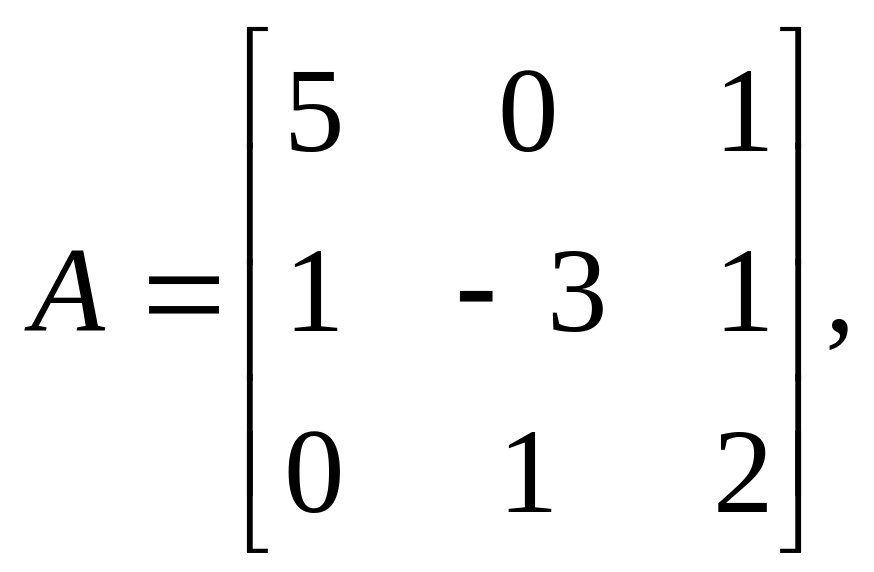

1
 4. 22.
4. 22.


1
 5. 23.
5. 23.
1


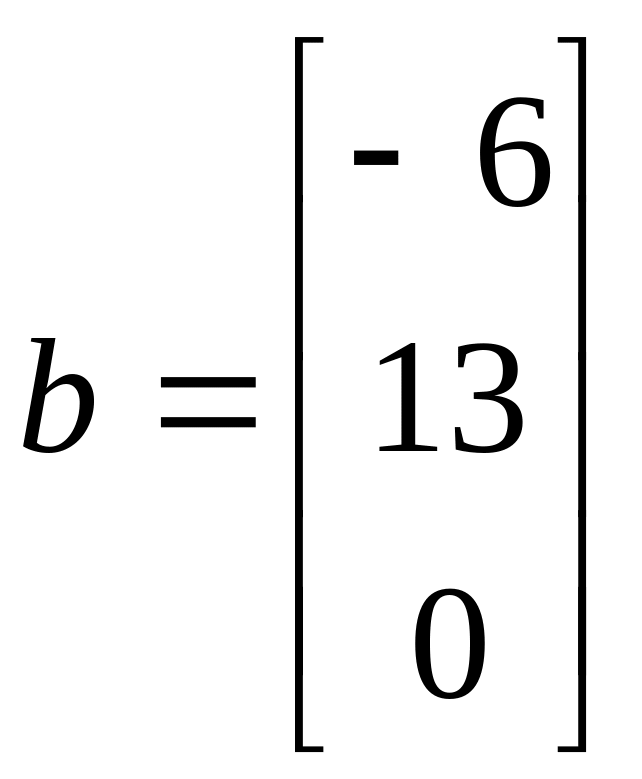 6. 24.
6. 24.
1
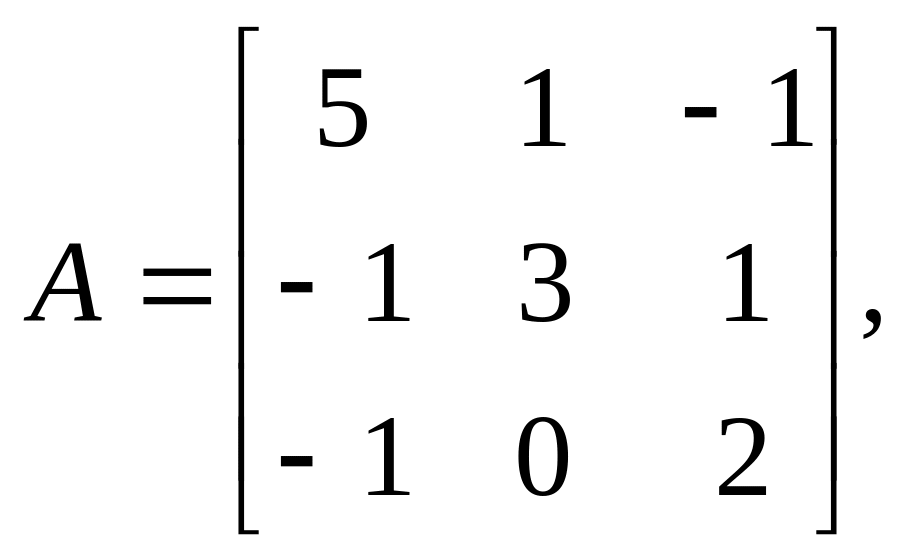

 7. 25.
7. 25.
1
 8.
8.
Тема 3: Решение нелинейных уравнений
Задание:
Методом
половинного деления, методом хорд,
методом итераций найти решения
уравнений с точностью
![]() =10-2
.
=10-2
.
x4 – 3x – 20 = 0 (x>0).
x3 – 2x – 5 = 0 (x>0).
x3 + 3x + 5 = 0
x4 + 5x – 7 = 0 (x>0).
x3 – 12x – 5 = 0 (x>0).
x3 –2x2– 4x + 5 = 0 (x<0).
x + ex = 0
x5 – x – 2 = 0
x3 – 10x + 5 = 0 (x<0).
2 – ln(x) – x = 0
x3 + 2x – 7 = 0
x3 + x2– 11 = 0 (x>0).
x4 – 2x – 4 = 0 (x>0).
2ex + x – 1 = 0
x4 – 2x – 4 = 0 (x<0).
2x3 + x2– 4 = 0 (x>0).
ex - x – 2 = 0
 ex
- x – 1 = 0 (x>0)
ex
- x – 1 = 0 (x>0)x2– cos(x) = 0 (x>0).
x2 + ln(x) = 0
ln(x) + 0,5x - 1= 0
ln(x) - 0,5x + 1= 0 (x>1).
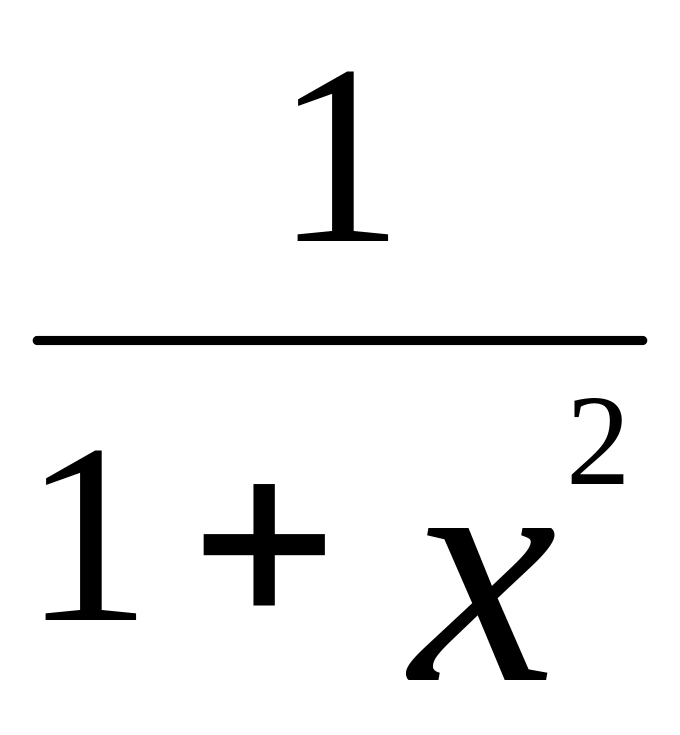 -
ln(x) = 0
-
ln(x) = 0 -
 = 0 (x>0)
= 0 (x>0) -
ln(x)
= 0
-
ln(x)
= 0
