Правило II.
Нехай функцiя
визначена, неперервна i диференцiйовна
в усiх точках простору
.
Щоб знайти глобальний мiнiмум (максимум) функцiї на всьому просторi , потрiбно:
1) знайти всi стацiонарнi точки функцiї , тобто розв'язати систему рiвнянь
; (3)
2) якщо система (3) не має розв'язкiв, то функцiя не має екстремумiв; якщо система (3) має розв'язки, то провести додаткове дослiдження i визначити, якi з стацiонарних точок є точками локального мiнiмуму (максимуму); при цьому, якщо цiльова функцiя має неперевні частиннi похiднi першого і другого порядку в околi стацiонарної точки, то для такого дослiдження можна використати достатнi умови екстремуму;
3) знайти значення функцiї у точках локального мiнiмуму (максимуму) (якщо такi точки iснують);
4) серед усiх знайдених значень функцiї вибрати найменше (найбiльше).
При розв'язуваннi задач умовної
оптимiзацii, коли допустима множина X
є пiдмножиною простору
,
знайти точки екстремуму значно складнiше
навiть коли множина X
обмежена і замкнена.
Формально загальне правило розв'язування таких задач можна одержати з правила II, замiнивши пункт 4 на такий:
- знайти найменше (найбiльше) значення цiльової функцiї на межi множини X , далі знайти значення, яких функцiя набуває в точках локальних мiнiмумiв (максимумiв), i вибрати найменше (найбiльше) серед усіх так знайдених значень.
Однак класичними методами це вдається зробити лише у випадках, коли множина X має досить просту структуру або задається як множина розв'язкiв деякої системи рiвнянь (принцип Лагранжа).
4. Основні засоби пакету Mathcad щодо розв’язування задач оптимізації.
В системі Mathcad екстремальні задачі можна розв’язувати за допомогою класичних методів, при цьому розв’язок можна одержати не лише у чисельному, а й в аналітичному вигляді.
Приклад 1. Розв’язати задачу Тартальї:
роздiлити число 8 на двi такi частини, щоб добуток їх добутку на їх рiзницю був максимальним,
за допомогою класичного методу (див. правило І) в аналітичному і чисельному вигляді
Розв’язування.
На рис. 2 показано знаходження розв’язку задачі Тартальї класичним методом за допомогою системи Mathcad, при цьому x1 – точка максимуму функції f(x), оскільки друга похідна в точці x1 менше нуля, а x2 – точка мінімуму, оскільки друга похідна в точці x2 більше нуля.
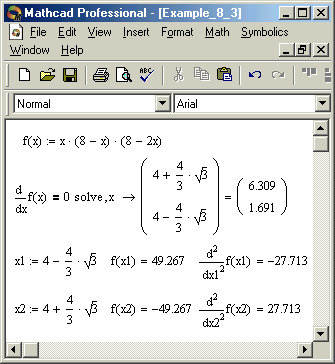
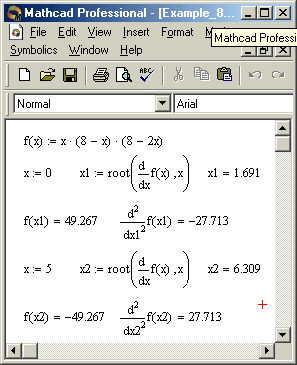
Рис. 2.
При
розв’язуванні задачі було використано
операції диференціювання
,
– для знаходження першої і другої
похідних функції
,
команду solve
для розв’язування рівняння
,
яка активізується або через систему
меню Symbolics\Variable\Solver,
або за допомогою панелі Symbolic,
а також функцію root(f(var), var, [a, b]),
за допомогою якої знаходяться наближені
корені рівняння виду f(var)=0
на проміжку [a,
b] відносно змінної var.
З а у в а ж е н н я.
Для знаходження всіх коренів многочлена
n-го
степеня виду
в системі Mathcad можна
використовувати функцію polyroots(a),
де
– вектор-стовпчик
коефіцієнтів заданого многочлена.
П р и м і т к и.
В системі Mathcad для наближеного розв’язування систем нелінійних рівнянь можна використовувати також функцію Minerr(var1, var2, ..., varN).
Для розв’язування систем лінійних рівнянь виду
можна використовувати функцію
lsolve(A,b),
де A
– невироджена квадратна матриця
коефіцієнтів системи, b
– вектор-стовпчик вільних членів
системи рівнянь.
Також для розв’язування задач оптимізації за допомогою системи Mathcad використовуються вбудовані функції Maximize і Minimize, які мають такий синтаксис:
Minimize(f, var1, var2, ..., varN),
Maximize(f, var1, var2, ..., varN),
де f – ім’я цільової функції задачі, var1, var2, ..., varN – змінні, від яких залежить цільова функція.
Результатом виконання функцій Minimize і Maximize є вектор-стовпчик, який є точним або наближеним розв’язком задачі відшукання відповідного екстремуму функції f із заданою точністю.
При розв’язуванні задачі оптимізації у вікні редактора Mathcad треба спочатку задати вхідні дані задачі (значення констант, векторів, матриць), цільову функцію та початкові значення змінних, від яких вона залежить. Потім, якщо розв’язується задача умовної оптимізації, записати службове слова Given, яке визначає початок розв’язкового блоку (solve block), і після нього записати обмеження задачі (обмеження-рівняння, обмеження-нерівності, прямі обмеження). При цьому запис можна здійснити у векторному або матричному вигляді.
Коли цільова функція і обмеження задачі (якщо вони є) описані, записується одна з функцій оптимізації (Maximize() або Minimize()) за правилами відповідного синтаксису. Причому можна відразу отримати результат, натиснувши на клавішу «=», або надати одержане значення змінній, яку можна використати при подальших обчисленнях, наприклад, для знаходження значення цільової функції в оптимальній точці.
При розв’язуванні задач нелінійного програмування, вказавши за допомогою мишки на функції Maximize або Minimize, в контекстному меню можна обрати один з ітераційних методів пошуку екстремуму, зокрема метод лінійних наближень, метод квазіньютонівських наближень, метод спряжених градієнтів, метод квадратичних наближень.