Лабораторная работа №3 "Испытание балки на прочность по наклонному сечению"

Цель работы изложена выше (см. стр.11)

К онструкция балки представлена на рис. 2.4, установка приборов и схема, схема загружения на рис. 3.1, где Т1-Т4-тензомеры, П-1 – прогибомер.

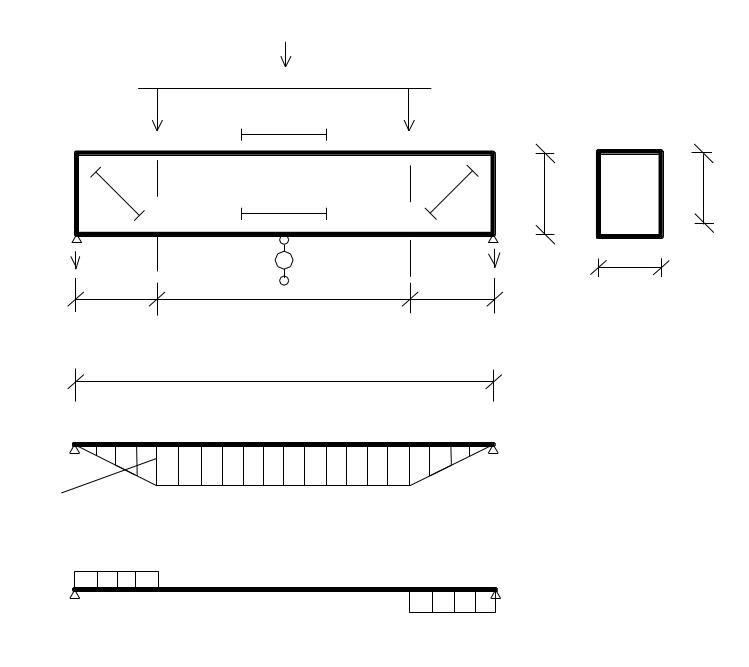
Рис 3.1

3.1 Теоретический расчёт балки.

3.1.1 Определение разрушающей поперечной силы, воспринимаемой хомутами и бетоном сжатой зоны .

Расчёт ведётся с использованием реальной конструкции образца балки. Данные для расчёта – в табл. 2.1. Погонное усилие, воспринимаемое хомутами (поперечными стержнями).

, H/см, где

- расчётное сопротивление поперечной арматуры, МПа.

- площадь поперечного сечения одного хомута, см².

- число плоскостей среза (на рис. 2.4) n=1;

- шаг хомутов, см.

Теоретическая оперечная сила, воспринимаемая совместно хомутами и бетоном сжатой зоны

, H, где R_bt – расчётное сопротивление бетона на растяжение [табл. 2.1 или (0,1-0,18)В]

3.1.2. Определение теоретической поперечной силы при появлении первых наклонных трещин .

Исходя из средних касательных напряжений

, при

; получим H.

3.1.3. Определение теоретической ширины раскрытия наклонных трещин .

Определить величину , наклонной к продольной оси в изгибаемых элементах с привлечением относительно точного математического аппарата довольно сложно. Поэтому в нормах проектирования используются эмпирические зависимости, основанные на экспериментальных данных, т.е. наиболее близких к достоверности.

В общем случае величина определяется по формуле:

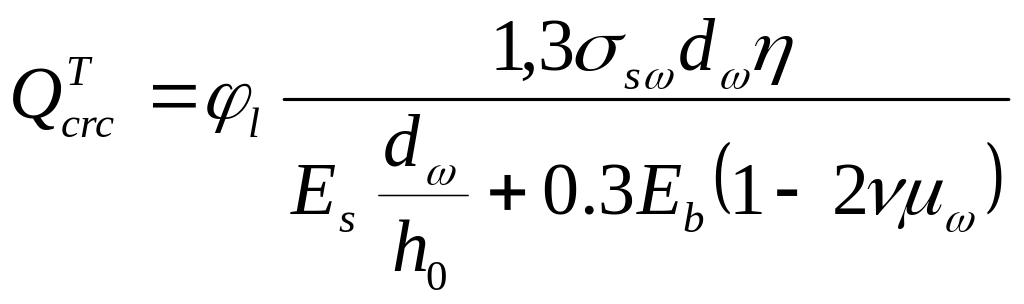_, где (кратковременное действие нагрузок);

1(при арматуре периодического профиля); 1,2 (при проволочной арматуре класса В_рI);

1,3 (при гладкой арматуре); = диаметр хомутов, см.; = модуль упругости арматуры хомутов ( =2·10⁵МПа – среднее значение); = по данным работы №1или по СНиП 2.03.01-84*.

– коэффициент приведения; , где – шаг хомутов, см; - площадь сечения хомутов; = напряжение в хомутах, которое в предварительных расчётах можно принимать = 0,45 , МПа.

Учитывая все приведённые значения, формула для определения при чомутах из гладкой арматуры упрощается до вида:

Более точное значение напряжения в хомутах можно проконтролировать и уточнить по формуле , где = 1,2 ; при , равной предполагаемой проекции наклонной трещины на горизонталь (см. рис. 3.1, т.е. около 2h).

3.2. Порядок проведения испытаний.

При проведении лабораторной работы №3 порядок проведения испытаний тот же, что при выполнении работы №2.

Поскольку целью работы является определение прочности балки по наклонным сечениям, особое внимание уделяется поведению приопорной зоны на длине «а» от опоры до груза (слева и справа).

Попутно можно фиксировать поэтапный рост прогибов, теоретическое значение которых можно вычислять так же, как в работе №2.

Характер трещинообразования фиксируется на развёртке, аналогично рис. 2.9.

Графики зависимости различных параметров от нагрузки (в виде Р, М и т.д.) выполняются аналогично работе №2 (по заданию руководителя и по спецзаданию отдельным исполнителям).

Литература: см. приложение 3.