Решение:

а) найдем из условий и

Получим систему уравнений:

Xi	− 6	− 1	2	5	10
Pi	0.1	0.1	0.2	0.4	0.2

.

б) для ряда распределения:

строим многоугольник распределения:

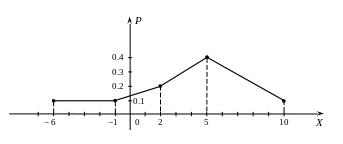
в) интегральную функцию строим с помощью свойства :

при
при
при
при
при
при

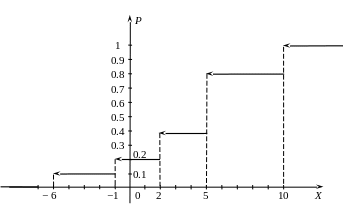
г) дисперсия .

(по условию) и

среднее квадратическое отклонение .

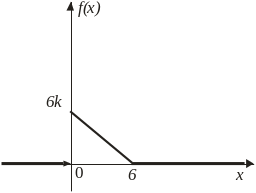
8. Задана дифференциальная функция (плотность) распределения

Найти:

а) параметр ;

б) интегральную функцию ;

в) математическое ожидание и дисперсию ;

г) вероятность события .

Решение:

а) из условия

тогда

б)

При построении воспользуемся свойством

.

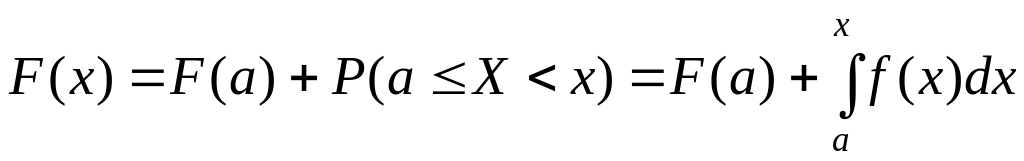При
при
при	.

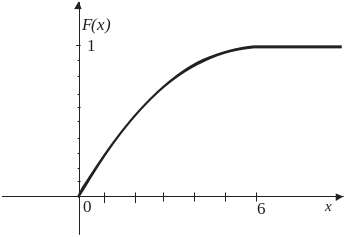
в) .

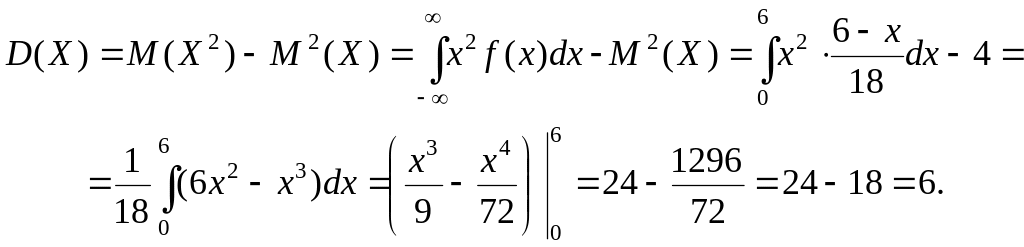
г) .

9. На запуск двигателя тратится в среднем 2.5 попытки. Считая, что вероятность запуска в каждой попытке одинакова, найти вероятность запуска двигателя не более, чем за 3 попытки.

Здесь имеет место геометрическое распределение случайной величины Х равной числу попыток до запуска двигателя, причем . Тогда из и .

10. Случайная величина Х имеет биномальное распределение (распределение Бернулли) с математическим ожиданием и дисперсией . Найти вероятность события .

Для биномального распределения ,

получим систему уравнений:

, тогда и .

Искомую вероятность находим с помощью формулы Бернулли.

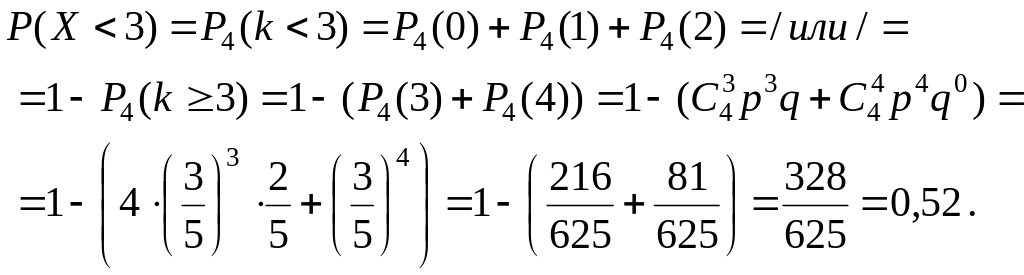
11. Для случайной величины Х, имеющей распределение Пуассона вероятность события равна 0.4. Найти вероятность события .

Из формулы для ,

Тогда

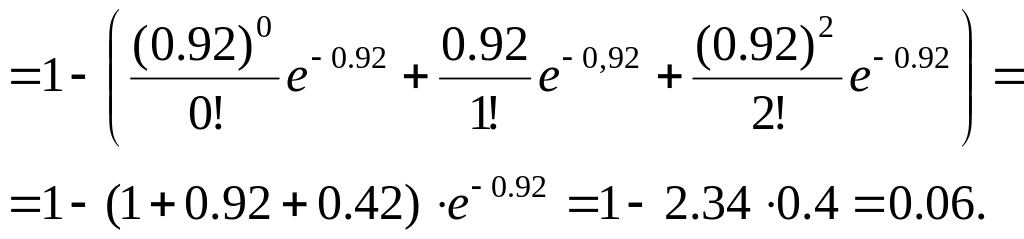
12. Случайная величина Х имеет равномерное распределение в интервале , причем и . Найти вероятность события .

Для равномерного распределения , .

По условию

. Для и интегральная функция имеет вид:

13. Случайная величина Х имеет показательное распределение и при этом численно . Найти вероятность события .

Из формул , или .

Тогда и интегральная функция будет:

14. Методами математической статистики установлено, что для данного региона роста призывников в ряды вооруженных сил имеют нормальное распределение с параметрами . Найти ожидаемое число призывников 3-го роста из 1000 человек.

Отметим, что третий рост соответствует интервалу (167, 173).

По формуле получим

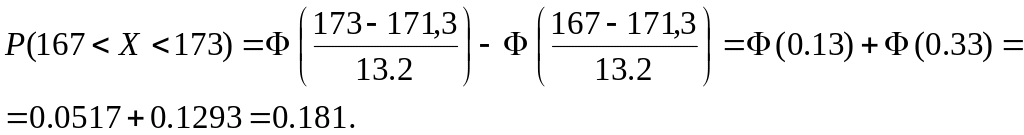
Тогда ожидаемое число призывников третьего роста

человек.

Примечание: значения и взяты из таблицы значений функции Лапласа .

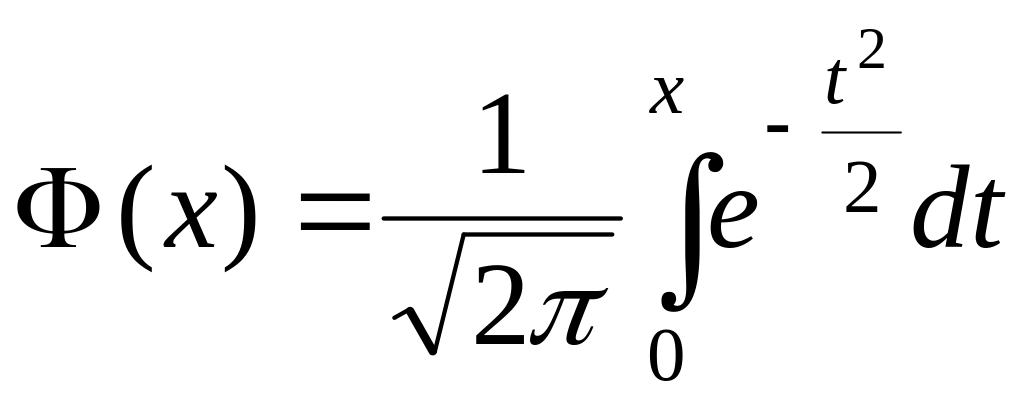6. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА.

Справочный материал.
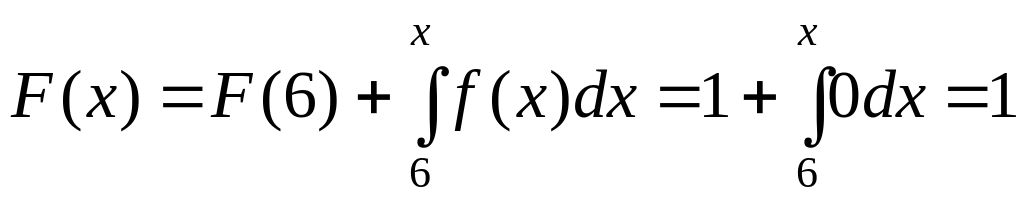