ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТУРИЗМА И СЕРВИСА»

ФГОУВПО «РГУТиС»

Кафедра МАТЕМАТИКА И ИНФОРМАТИКА

(название кафедры)

УТВЕРЖДАЮ

Проректор по учебной работе,

д.э.н., профессор

_________________________Новикова Н.Г.

«_____»_______________________200__г.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ

(ЧАСТЬ 5)

для студентов очной, заочной формы обучения и по форме экстернат

Дисциплина

ТЕОРИЯ ВЕРОЯТНОСТЕЙ, МАТЕМАТИЧЕСКАЯ СТАТИСТИКА, ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

(название дисциплины)

Для всех специальностей

Москва 2008 г.

Методические указания по выполнению контрольных работ составлены на основании рабочих программ дисциплины

ТЕОРИЯ ВЕРОЯТНОСТЕЙ, МАТЕМАТИЧЕСКАЯ СТАТИСТИКА, ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

(название дисциплины)

Методические указания по выполнению контрольных работ рассмотрены и утверждены на заседании кафедры МАТЕМАТИКА И ИНФОРМАТИКА

(название кафедры)

Протокол № 9 «22» апреля 2008г.

Зав кафедрой к.т.н. доцент, Щиканов А.Ю.

Методические указания по выполнению контрольных работ одобрены Учебно-методическим советом ФГОУВПО «РГУТиС»

Протокол № ________ «____»_______________200_г.

Методические указания по выполнению контрольных работ разработаны:

Преподаватели кафедры

Математика и информатика

(название кафедры)

доцент Белов Б.А.,

Согласовано:

Зам. проректора - начальник

Учебно-методического управления к.э.н., доцент Дуборкина И.А

Начальник

Методического отдела Рыженок Н.В.

5. Теория вероятностей.

Справочный материал.

Случайные события:

- вероятность события P(A) = , n – число всех единственно возможных и равновозможных исходов испытания, а m – число исходов благоприятствующих появлению события А;

P_n = n! - число перестановок n различных элементов

( n! = 1 ∙ 2 ∙ 3 ∙ ∙ n, при этом 0! = 1 );

число размещений m различных элементов в n местах

(m ≤ n);

число сочетаний по m элементов из n различных

элементов ( m ≤ n, );

А + В – это событие, состоящее в появлении А или В или А и В вместе;

А ∙ В – это событие, состоящее в появлении А и В вместе;

– это событие противоположное А;

Р(А+В) = Р(А) + Р(В) для несовместных событий А и В;

Р(А+В) = Р(А) + Р(В) − Р(А∙В) для совместных событий А и В;

Р(А∙В) = Р(А) ∙ Р(В) для независимых событий А и В;

Р(А∙В) = Р(А)∙Р для зависимых событий А и В, где Р – условная вероятность появления события В при условии, что событие А

уже появилось;

формула Бернулли для вычисления вероятности появления события А ровно раз в серии из n испытаний, при этом

Р(A) = p в каждом испытании, Р( ) = q, p + q = 1;

Р(А) = - формула полной вероятности, при этом гипотезы H_i образуют полную группу событий, то есть они попарно

независимы и , а событие А происходит только с одной из гипотез H_i;

- формула Байеса для вычисления вероятности гипотезы Н_к при условии, что событие А произошло.

Случайные величины.

Дискретная случайная величина (ДСВ):

X принимает изолированные числовые значения x1, x2 , .... ;

- ряд распределения ДСВ – это таблица вида:

xi	x1	x2	....
Pi	P1	P2	...

при этом

- многоугольник распределения – это ломаная, соединяющая точки ( );

- интегральная функция F(x) = P(X < x) = F(a) + P(a ≤ X < x) представляет собой ступенчатую кривую;

- математическое ожидание ДСВ определяется формулой ;

- свойства: M(С) = C, M(hX + C) = h ∙M(X) + C;

- дисперсия D(X) = M(X − M(X))² = M(X²) − M²(X);

- расчетные формулы: D(X) ;

- свойства: D(X) ≥ 0, D(0) = 0, D(h∙X + c) = h² ∙D(X);

- среднее квадратическое отклонение ; Основные виды распределений ДСВ.

1. Геометрическое: X = k = 1, 2, 3...

,

2. Распределение Бернулли (биноминальное): X = k = 0, 1, 2, ..... , n

M(X) = n ∙ p, D(X) = n ∙ p ∙ q, ;

3. Распределение Пуассона: X = k = 0, 1, 2, ... , n

M(X) = a, D(X) = a,

Непрерывная случайная величина (НСВ):

X принимает числовые значения ;

- плотность (дифференциальная функция) распределения вероятностей:

- интегральная функция распределения:

F(x) = P(X < x) = , при этом ;

- вероятность попадания НСВ в интервал

P(α < X < β) = F(β) – F(α) =

- математическое ожидание M(X) =

- дисперсия D(X)

- среднее квадратическое отклонение .

Основные виды распределений НСВ:

1. Равномерное распределение в интервале (a, b)

при

при

при

при

при a x b,

при ,

M(X) = D(X) = , ;

1. Показательное распределение

при

при

при

при

M(X) = , D(X) = ,

2. Нормальное распределение

F(x) = 0.5 + Ф( ), где Ф(z) = 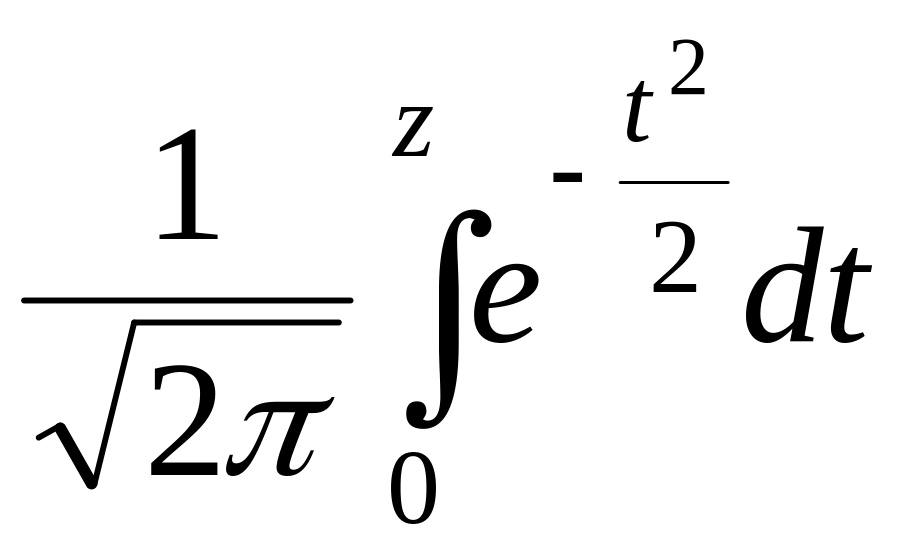– функция Лапласа (ее значения имеются в приложениях учебников по теории вероятностей);

M(X) = a, D(X) = , ,

P(α < X < β) = Ф – Ф .