1.7. Предельные возможности блоковых кодов

Знание теоретического предела исправляющей возможности кодов позволяет судить о том, целесообразно ли в той или иной ситуации применять помехоустойчивое кодирование.

Добавляя проверочные символы, мы тем самым уменьшаем скорость передачи информации, вводим избыточность. Оценкой изменения скорости может служить отношение k/n. Одновременно увеличение числа проверочных символов, а следовательно, и увеличение n должно приводить к росту кодового расстояния. Это, в свою очередь, влечет за собой повышение исправляющей способности кода, так как кодовое расстояние и исправляющая способность кода связаны однозначно

.

При больших кодовых расстояниях d можно считать, что

Относительный рост исправляющей способности кода оценивается как

Очевидно, что с ростом d/2n должно уменьшаться отношение k/n. Представляет большой интерес найти границу этой связи. Возможны оценки сверху определяет максимальную скорость передачи информации k/n (или, что то же самое, минимальную избыточность) при требуемой исправляющей способности кода d/2n. Граница снизу для k/n, напротив, отмечает предельно плохие показатели кодов.

В литературе известно несколько таких оценок. Рассмотрим определение верхней границы по Хэммингу [2].

Пусть задан линейный блоковый (n,k) код, который содержит кодовых слов. Декодирование этого кода можно производить с помощью таблицы декодирования. Это таблица содержит смежных класса. Предположим, что код исправляет все ошибки кратности t. Это значит, что все векторы веса t и меньше (те, у которых 1 стоит не более чем на tпозициях) должны быть образующими смежных классов.

Если обратиться к таблице декодирования (1.18), то в ней среди слов Е, должно быть все

слова веса t и меньше. Число таких слов равно и оно должно быть меньше числа а смежных классов

Или

(1.19)

Для выяснение предельных возможностей кодов надо оценить сумму в (1.19). Определим число сочетаний при больших значениях n

Обозначим t/n=λ и µ=1-λ. Тогда t=nλ, n-t=µn.

(1.20)

При n»1 величину n! можно приближенно оценить по формуле Стирлинга

Тогда формула (1.20) преобразуется к виду

При большом n очевидно, что

Обратившись теперь к соотношению (1.19), запишем цепь неравенств

Или n-k

Раскроем последнее соотношение

.

(1.22)

Или

.

Соотношение (1.22) называется верхней границей Хэмминга. На рис 1.5 ей соответствует кривая 1

Другая известная оценка-граница Плоткина:

Ей соответствует прямая 2 на рис. 1,5. Нижняя оценка для скорости передачи k/n дается границей Варшамова-Гилберта (кривая 3 на рис. 1,5)

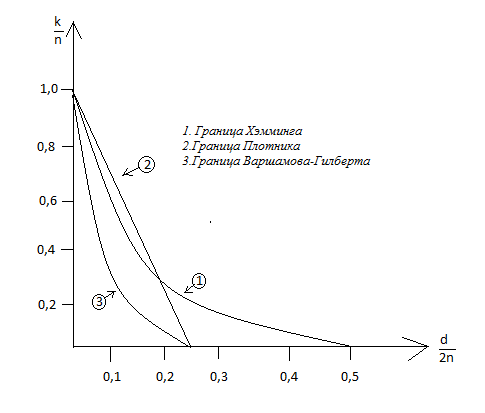
Рис. 1.5. Границы для минимального расстояния блоковых кодов (n 1)

Необходимо еще раз подчеркнуть, что все эти оценки носят асимптотический характер; они справедливы только при (n, t, d) 1.