1.4 Геометрическая интерпретация кодирования и декодирования
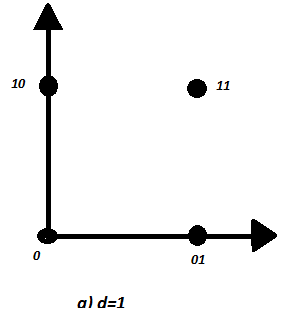
Процесс исправления и обнаружения ошибок удобно представить геометрически [7]. Сопоставим каждой кодовой комбинации точку в n- мерном пространстве (n- длина кодовой комбинации). Все множество кодовых комбинации длины n образует n- мерный куб. Если n=k ,то во всех вершинах этого куба расположены разрешенные кодовые комбинации. Такой случай показан на рис. 1.4, a для n=k=2.
Расстояние между двумя кодовыми комбинациями равно числу ребер куба между соответствующими вершинами. Для кода на рис. 1.4, а d=1.
Мы
видели, что для обнаружения ошибок
необходимо выполнить условие n
k.
При
этом часть вершин куба окажется незанятой.
Свободные вершины соответствуют
запрещенным кодовым комбинациям. Причем
запрещенные комбинации надо выбирать
таким образом, чтобы они разделяли
разрешенные комбинации. Пример кода,
обнаруживающего одиночные ошибки,
показан на рис. 1.4,б. Этот код определен
соотношением (1.2).
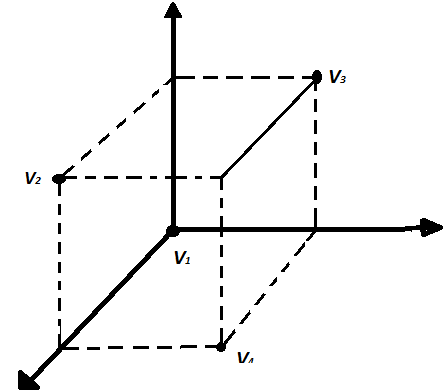
Из рисунка видно, что между любой парой разрешенных кодовых комбинаций лежит одна запрещенная. Кодовое расстояние здесь равно d=2. Однократная ошибка соответствует перемещению по одному ребру в соседнюю вершину. Для этого кода такое перемещение всегда приводит к запрещенному слову.
Для
сравнения на рис. 1.4,в дан пример неудачно
составленного кода. Здесь есть соседние
разрешенные вершин (
)
и в то же время
.
У такого кода кодовое расстояние равно
1, и он не может обнаружить все однократные
ошибки. В общем случае кратность
обнаруживаемых ошибок определяется
соотношением
(1.6)
Отсюда кодовое расстояние должно удовлетворять условию.
(1.7)
Для исправления ошибок требуются большие кодовые расстояния. На рис. 1.4,г показан пример кода (3,1), исправляющего одиночные ошибки.
Б) d=2
В) d=1
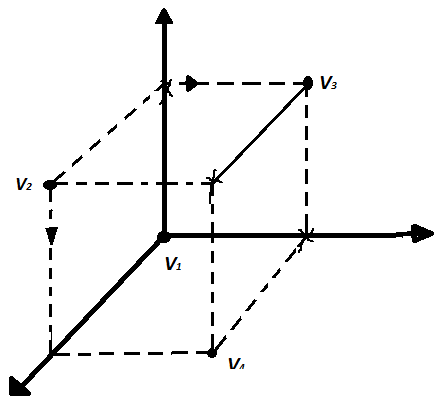
Г) d=3
Рис. 1.4. Геометрическое представление кодов
Для
исправления ошибок все вершины делятся
на 2 группы: одна – ближе к слову
другая
к слову
(на рисунке они отмечены кружками и
крестиками). Если на вход декодера
поступает кодовая комбинация из первой
группы, то принимается решение,
соответствующее
.
В противном случае принимается решение
.
Таким образом будут исправлены все
однократные ошибки.
В
общем случае для исправления ошибок
кратности
необходимо, чтобы между разрешенными
вершинами лежало не меньше, чем
ребер куба [8], т.е.
(1.8)
Или
,
(1.9)
Где [ ] означает целую часть числа.
Линейные блоковые коды
Мы будем достаточно подробно изучать только один класс блоковых кодов – линейные блоковые коды.
Код называется линейным, если проверочные символы образуются как линейная комбинация информационных. Остановимся на этом подробнее.
В общем случае основанием кода может быть любое простое число. Но в большинстве практически интересных случаев основание кода равно 2, т.е. коды являются бинарными. Все операции над символами выполняются по mod2. В дальнейшем будут рассмотрены необходимые понятия алгебры. Пока же нам потребуется только знание правил сложения и умножения по mod2.
В бинарных кодах символы могут принимать только 2 значения {0, 1}. Правила сложения и умножения определяются следующим образом:
0+0=0;
1+0=1; 1
(1.10)
0+1=1;
1+1=0; 1
Пусть
кодовое слово содержит n
символов:
…,
.
Как во всяком блоковом коде, k
символов
этого слова являются информационными.
Пусть это будут символы
…,
.
Остальные символы проверочные :
…,
.
Для линейного кода вычисление этих проверочных символов производится так:
(1.11)
,
,
Рассмотрим в качестве примера бинарный код (7,3), который строится по правилу
;
;
;
;
Для
каждой комбинации информационных
символов {
}
по этому правилу можно определить
проверочные символы. Например, если
;
,
то
;
и все кодовое слово запишется следующим
образом: 1011010.
Очевидно, что описывать код путем перечисления соотношений (1.11) неудобно. Наиболее удобным и распространенным способом задания кодов является матричный.
Рассмотрим
этот способ на примере того же кода
(7,3),определяемого соотношениями (1.12).
Общее число разрешенных кодовых
комбинаций (включая нулевую) равно числу
информационных слов; в нашем примере
.
Запишем все нулевые информационные
слова:
100; 010; 001; 110; 011; 111; 101.
Из них можно выделить k=3 линейно- независимых слов, причем по- разному.
Например, 100;010; 001
Или 111; 100; 110 и т.д.
Все остальные информационные слова получаются как линейная комбинация этих линейно- независимых слов.
Таким
образом, при линейном кодировании
достаточно записать кодовые комбинации
для k
линейно- независимых информационных
слов и все остальные получать путем их
линейной комбинации. K
линейно- независимых кодовых комбинаций
называются базисными векторами. Их
располагают в виде матрицы размером
(
),
которая называется базисной матрицей,
или порождающей. В зависимости от того,
какие информационные слова взяты за
базисные, получатся и разные матрицы.
В качестве примера запишем2 порождающие
матрицы для кода (7,3), проверочные символы
которого определяются в соответствии
с правилом (1.12):
;
;
Можно показать, что для этого кода существует всего 29 вариантов порождающих матриц. Путем линейной комбинации строк порождающей матрицы получается любое кодовое слово.
Если
в качестве порождающей использовать
матрицу
,
то информационные и проверочные символы
окажутся разделенными. Матрица такого
вида называется приведенно- ступенчатой.
Условно ее можно представить как
сочетание единичной матрицы
I
размером
)
и матрицы P
размером
(
),
состоящей из проверочных символов:
(1.13)
Кодовое слово (кодовый вектор) U получается в результате перемножения информационного вектора K на матрицу G
(1.14)
Порядок вычислений (1.14) соответствует правилам матричного умножения, но все операции выполняются по mod2. Например, для информационного вектора К=[101] в коде (7,3) это произведение равно
KG=
=
Наряду с порождающей матрицей G, код может задаваться также проверочной матрицей H, которая должна удовлетворять соотношению
(1.15)
Знак
Т
означает
операцию транспонирования. Матрица Н
имеет
размерность (
).
Из
соотношений (1.14) и (1.15) следует, что каждое
кодовое слово, умноженное на
,
дает нулевой вектор
.
Поскольку каждый код имеет несколько порождающих матриц, то им соответствует столько же проверочных матриц. В дальнейшем будет использоваться только проверочная матрица, соответствующая приведенно- ступенчатой форме порождающей матрицы.
Если использовать символику (1.13), то проверочную матрицу можно представить в виде
(1.16)
Например, для кода (7,3)
Можно
проверить ортогональность кодовых
векторов и матрицы
0 0 0 1
В проверочной матрице единицы указывают, какие символы кода участвуют в той или иной проверке. Действительно, каждый линейный код удовлетворяет своему правилу (1.11).
Для двоичных кодов из (1.11) следует, что
.
(1.17)
Именно
эти соотношения и отражения в строках
матрицы Н.В
каждой строке первые к
позиций занимают символы
,
затем стоит 1 в матрице
на месте проверочного символа. С помощью
матрицы Н
в
принятом кодовом слове проводится r=n-
k
проверок
на четность. Если ошибок нет, то в каждой
из r
проверок
(1.17) выполняется также при четном числе
ошибочных символов. Если в проверку
попадает нечетное число ошибочных
символов, то соответствующее равенство
(1.17) не выполняется и при этой проверке
получится 1.
Например, пусть ошибка произошла в четвертом символе кодового слова U=[1 0 1 0 0 1 0], т.е. принято слово V=[ 0 1 0 0 1 0 ]. При вычислении произведения получаем
.
Здесь ошибочный символ участвовал только в первой проверке.