1 2 K2 k1 2 1 Рис. 4.14. Схемы кодирования для кода бчх (15,7)

4.3. Декодирование циклических кодов

Процесс декодирования – поиск и исправление ошибок – наиболее сложная операция при использовании помехоустойчивого кодирования.

Схемы, реализующие декодирование, могут базироваться на использовании как проверочного полинома h(x), так и образующего полинома g(x) [5]. Рассмотрим сначала принцип построения декодеров.

Пусть кодовая комбинация описывается полиномом U(x)(U(x) принадлежит коду), а кодовой комбинации ошибок соответствует полином Е(х), т.е. на входе декодера присутствует комбинация, описываемая полиномом

V(x)=U(x)+E(x)

Умножим V(x) на проверочный полином h(x)

V(x)h(x)=U(x)h(x)+E(x)h(x);

U(x)h(x)=0

Поэтому, если Е(х) не принадлежит коду, то результат умножения отличен от нуля.

В разделе 1.6 отмечалось, что исправление ошибки возможно только тогда, когда комбинация Е является образующим смежного класса.

Аналогичные рассуждения можно провести и для декодирования с использующего полинома g(x). Разделим V(x) на g(x). Если V(x) принадлежит колу, то деление осуществляется без остаток, но нему надо восстановить ошибочную комбинацию Е.

Наиболее простые решения получаются для исправления одиночных ошибок. Проследим эту процедуру при использовании проверочной матрицы Н (т. е. с помощью полинома h(x))

При одинаковых ошибках вектор ошибки E содержит 1 только на одной позиции.

В результате умножения получается одна строка матрицы . Очевидно, нетрудно построить схему, селектирующую нужные комбинации и тем самым указывающую, на какой позиции произошла ошибка. Однако для циклических кодов достаточно иметь селектор только одной комбинации.

Действительно, если - кодовое слово, то его циклическая перестановка также является кодовым словом. Если производить циклические сдвиги принятого слова , то будут получаться суммы некоторого кодового слова и ошибки, смещенной на позиций:

Пусть имеется селектор, фиксирующий какую- то определенную ошибочную комбинацию (например, 1 в первом символе). Производя циклические сдвиги принятой кодовой комбинации и каждый раз вычисляя (или остаток от деления на ), через несколько циклов получим селектируемую комбинацию. Число этих циклов равно номеру позиции, в которой произошла ошибка. Схема декодера, реализующего этот принцип, показана на рис. 4.15. Вычисления производятся в следующей последовательности:

1. Принятая кодовая комбинация вводится в буферный регистр и в контрольное устройство, вычисляющее или , или .

2. Если в результате произведенных действий во всех элементах контрольного устройства получаются нули или деление на проводится без остатка), то это значит, что ошибок нет и принятая комбинация выводится из буферного регистра.

3,а. Если в контрольном устройстве зафиксирована комбинация, отличная от нуля и совпадающая с селектируемой комбинацией, то это значит, что ошибка произошла на первой позиции. При этом селектор вырабатывает 1, которая складывается с первым символом принятой кодовой комбинации, тем самым ошибка исправляется.

3,б. Если отличная от нуля комбинация в контрольном устройстве не совпадает с селектируемой комбинацией, то это означает, что ошибка произошла не на первой позиции.

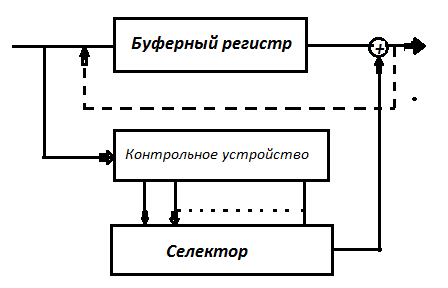
Тогда производится циклический сдвиг принятой кодовой комбинации на одну позицию, одновременно первый символ выводится на выход. В контрольном устройстве производятсявычисления для слова . Если получится селектируемая комбинация, то исправляется символ,находящийся в первой ячейке буферного регистра (второй символ принятой комбинации); если контрольная комбинация не селектируется, производится следующий сдвиг и т.д.

В силу автоматизма работы этого декодера, где бы ни находилась ошибка, каждое принятое слово должно подвергнутся проверке n раз (по числу разрядов в слове). Очевидно, что такая процедура декодирования занимает много времени.

Процесс декодирования может быть сокращен, если образующий полином кода неприводимый.

Мы видели (раздел 4.1), что схема деления на неприводимый полином при автономной работе формирует в строго определенном порядке все элементы расширения . Этим свойством можно воспользоваться при построении декодера. Рассмотрим процесс исправления одиночных ошибок на примере кода (7,4), имеющего образующий полином . Пусть в контрольном устройстве производится деление на полином g(x) равен (101). При дальнейшей автономной работе схемы ее состояние на следующем такте будет описываться комбинацией 100. Это селектируемая комбинация, которая сигнализирует о том, что выводимый из буферного регистра символ должен быть исправлен.

Если ошибка произошла во втором символе, то , остаток от деления на равен (111). Селектируемая комбинация 100 получится после двух тактов автономной работы схемы. На рис.4.16 показана структура такого декодера.

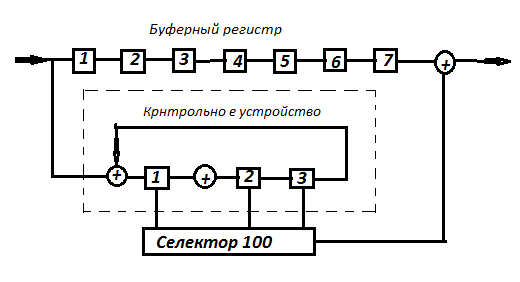
Последовательные состояния его элементов при подаче на вход безошибочной комбинации и комбинации с ошибкой на одной позиции приведены в табл.4.7.

Для исправления ошибок большой кратности предложены различные алгоритмы, которые по существу представляют собой специализированные вычислители для решения системы линейных уравнений, в которой неизвестными являются номера ошибочных позиций, а коэффициентами – строки матрицы . Эти устройства громоздки и с ростом числа исправляемых ошибок становятся все менее надежными. В связи с этим велись поиски кодов, которые позволят упростить процедуру декодирования. Было выяснено, что многие циклические коды допускают мажоритарное декодирование.

№ такта	Буферный регистр	Контрольное устройство				Выход селектора		Выход декодера
	1 2 3 4 5 6 7	1	2	3

Кодовая комбинация 1101001 без ошибки

1 2 3 4 5 6 7	1	0	0	0	0	0	0	1	0	0
	1	1	0	0	0	0	0	1	1	0
	0	1	1	0	0	0	0	0	1	1
	1	0	1	1	0	0	0	0	1	1
	0	1	0	1	1	0	0	1	1	1
	0	0	1	0	1	1	0	1	0	1
	1	0	0	1	0	1	1	0	0	0
8 9 10 11 12 13 14	0	1	0	0	1	0	1	0	0	0	0	1
	0	0	1	0	0	1	0	0	0	0	0	1
	0	0	0	1	0	0	0	0	0	0	0	0
	0	0	0	0	1	0	0	0	0	0	0	1
	0	0	0	0	0	1	0	0	0	0	0	0
	0	0	0	0	0	0	1	0	0	0	0	0
	0	0	0	0	0	0	0	0	0	0	0	1

Кодовая комбинация 1100001 с ошибкой на 4-й позиции

1 2 3 4 5 6 7	1	0	0	0	0	0	0	1	0	0
	1	1	0	0	0	0	0	1	1	0
	0	1	1	0	0	0	0	0	1	1
	0	0	1	1	0	0	0	1	1	1
	0	0	0	1	1	0	0	1	0	1
	0	0	0	0	1	1	0	1	0	0
	1	0	0	0	0	1	1	1	1	0
8 9 10 11 12 13 14	0	1	0	0	0	0	1	0	1	1	0	1
	0	0	1	0	0	0	0	1	1	1	0	1
	0	0	0	1	0	0	0	1	0	1	0	0
	0	0	0	0	1	0	0	1	0	0	1	1
	0	0	0	0	0	1	0	0	1	0	0	0
	0	0	0	0	0	0	1	0	0	1	0	0
	0	0	0	0	0	0	0	1	1	0	0	1

4.4. Мажоритарное декодирование

Мажоритарный принцип – это принцип принятия решения по большинству голосов.

Рассмотрим, как можно реализовать этот принцип, используя избыточность кода. Пусть система проверок задана с помощью проверочной матрицы H.Для кодового вектора U должно удовлетворятся равенство

Это равенство эквивалентно системе r проверок на четность

r проверок

Систему проверок можно видоизменить беря линейные комбинации равенств из (4.2). Предположим, что удается так подобрать эти комбинации, что некоторый символ входит во все проверки, а все остальные входят в проверки только по одному разу. Тогда символ можно выразить несколькими способами:

. . . . . . . . . . (4.3.)

Система (4.3) называется системой раздельных проверок.

Если таких соотношений , то исправляются все ошибки кратности t. Действительно, каждый символ входит только в одну проверку. Если искажено t символов, то искажено t проверок. Чтобы принять правильное решение относительно символа , надо иметь t+1 неискаженную проверку. Таким образом, общее число проверок должно быть .

В силу цикличности кода соотношение (4.3) позволяет принимать решения для всех символов.

Рассмотрим сначала простой код (7.3) с образующим полиномом

Нетрудно получить приведенно- ступенчатую форму его образующей матрицы

Ей соответствует проверочная матрица

Кодовую комбинацию на входе мы описываем или полиномом

Или вектором с компонентами

Матрица H определяет следующую систему проверок:

На основе этих проверок построим новую систему проверок, используя первое и третье равенства и сумму второго и четвертого

или

(4.5)

Последнее равенство в (4.5) является тривиальным. Система (4.5) образует систему раздельных проверок, позволяющих исправлять одиночные ошибки. Схема, реализующая этот принцип, показана на рис. 4.17. Мажоритарный орган М формирует на выходе символ 1, если на большинстве его входов появились 1. В противном случае формируется символ 0. Процесс декодирования осуществляется в следующем порядке. Сначала заполняются элементы регистра. Затем вычисляется первый символ (по большинству). После этого происходит циклический сдвиг на одну позицию и вычисляется второй символ и так 7 тактов.

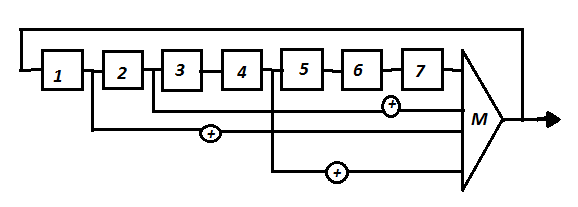
Проследим несколько тактов работы схемы на рис. 4.17, когда на вход поступает кодовая комбинация без ошибок и с ошибкой (см. табл.4.8, где звездочками отмечено, какие символы участвуют в проверке).

Таблица 4.8

Комбинация 1101001 без ошибок

№ проверки

Ячейки регистра

1 2 3 4 5 6 7

Входы мажоритарного органа

Символ на выходе

Такт 1

	1 0 0 1 0 1 1
1	* * * * * * *	1	1
2		1
3		1
4		1

Такт 2

	1 1 0 0 1 0 1
1	* * * * * * *	1	1
2		1
3		1
4		1

Комбинация 1001001 с ошибкой на второй позиции

Такт 1

	1 0 0 1 0 0 1
1	* * * * * * *	1	1
2		1
3		0
4		1

Такт 2

	1 1 0 0 1 0 0
1	* * * * * * *	1	1
2		1
3		1
4		0

Аналогично можно построить схему мажоритарного декодирования для исправления большего число ошибок. Примером этому может служить декодирование кода БЧХ (15,7), рассмотренного в разделе 3.3. Представим проверочную матрицу это го кода

Для сокращения записи обозначим строки матрицы как .

Систему раздельных проверок можно получить в результате следующих линейных комбинаций:

+

Система (4.6) определяет раздельные проверки для . В силу цикличности когда можно произвести 7 циклических сдвигов и получить удобную систему проверок

Покажем, что при использовании этого алгоритма возможно исправление двухкратных ошибок.

Одной из разрешенных кодовых комбинаций является следующая: 110000010011100

Пусть ошибочно приняты символы и , т.е. принятая комбинация такова: 010100010011100

Система проверок на такте 1 при определении первого символа представлена в табл. 4.9.

№ проверки	Ячейки регистра	010100010011100		Входы мажоритарного органа		Символ на входе
1 2 3 4 5			* * * * * * *		1 1 0 1 0		1

Таким образом,сформирован правильный символ.

Необходимо иметь в виду,что мажоритарное декадирование возможно не для всех кодов.Известны решения для кодов Хэмминга,некоторых кодов БЧХ,а также кодов Рида Маллера,близких по структуре к циклическим кодам.

Г Л А В А 5

Восросы целесообразности использования помехустойчивых кодов

Вопрос о целесообразности использования того или иногот помехоусатойчивого кода возникает каждый раз,когда решается задача оптимального проектирования системы передачи информации.Необхадимо иметь в виду,что различные органичения,которые накладываются на режим передачи и приема,могут привести к совершенно резным выводам о применимости того или иного кода.

Типичными внешними параметрами системы,т.е. требованиями к ней,являются скорость передачи информации и вероятность ошибки,пересчитанная на 1 бит передаваемой информации. Для выполнения этих требований необходимы некоторые расходы энергии и полосы.Энергетические затраты будем характиризовать величиной , равной.

, (5.1)

Где - энергия, затраченная на передачу 1 бит информации; - спектральная плотность шума на входе приемника.

Затраты полосы характеризуются отношением

, (5.2)

Где - полоса частот, занимаемых системой; - скорость передачи информации.

Очевидно, что система тем лучше, чем меньше ее параметры и . Однако редко удается выделить абсолютно лучшую систему, и проектировщик на основании дополнительных требований (сложность, стоимость и т.д.) должен сделать выбор из ряда нехудших систем.

Рассмотрим порядок анализа в предложении, что фиксирована мощность передатчика. Это требование в сочетании с требованием обеспечения скорости передачи R по существу ограничивает энергию одной кодовой группы.

Обозначим отношение энергии одного символа в кодовой группе без кодирования к спектральной плотности шума . В этом случае . Вероятность ошибки при приеме одного символа зависит от вида манипуляции в радиотракте и от способа приема, но в любом случае – это убывающая функция величины

Вероятность ошибки при приеме кодовой комбинации из символов составляет

P_кк =1- (1-P₀)^k.

Если перейти к помехоустойчивому кодированию и вводить проверочные символов, не изменяя скорости передачи,то длительность одного символа уменьшится и соответственно уменьшится энергия одного символов. Новое отношение сигнал/шум при приеме одного символа равно

В результете должна возрасти вероятность ошибки при приеме отдельного символа. Р₁.Необходимо выяснить результирующий эффект: увеличилась или уменьшилась вероятность ошибки при приеме всей кодовой комбинации с учетом исправляющей способности кода.

При кратности исправляемых ошибок t вероятность ошибочного приема всей кодовой комбинации равна

Р_{1 К К=}

При Р₁ <<1 это соотношение можно упростить

P_{1 K K}

Введение помехоустойчивого кодирования можно считать целесообразным, если вероятость ошибки, определяемая формулой,превышает вероятность ошибки по,т.е.

P_1кк <P_кк .

Однако в качестве внешнего параметра,как правило,задана вероятность ошибки на двоичный символ, Р_b .Связь P_1kk c P_b зависит от характера кодируемой информации, но при P_Ikk <<1 различные представления P_b оказываются практически равноценными . В дальнейшим считется, что

Вместо сравнения (5.6) удобнее сопоставлять вероятности ошибки на символ и считать введение кодирование целосообразным,если

Следовательно,надо выяснить,удовлетворяется ли неравенство

Рассмотрим два примера

Пример 1. Выясним,при каких вероятностях P₀ целесообразно использовать код Хэмминга (7,4). Будем считать,что для приема отдельных символов иппользуется некогерентная обработка и

Эта зависимость представлена на рис.5.1 кривой 1. Определим

=0,5 exp (-

Для рассматриваемого кода t=1

exp (- )

На рис. 5.1 эта зависимость представлена кривой. Из рисунка видно, что при некогерентной обработке сигнала

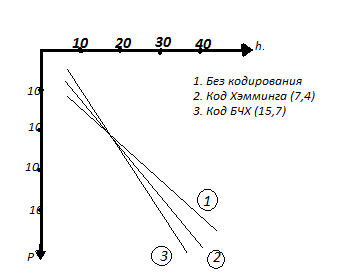
Рис. 5.1. Зависимость вероятности ошибки от отношения сигнал/шум

в приемнике рассматриваемый код целесообразно применять при , что соответствует вероятности ошибки на 1 бит .

Пример 2. Проведем аналогичный анализ для кода БЧХ (15,7). Для этого кода t=2

;

Эта зависимость представлена на рис. 5.1 кривой 3. Мы видим, что этот код также можно считать эффективным, начиная с Однако при различных требуемых коды будут обеспечивать различный энергетический выигрыш, который можно оценить следующим образом:

Где - требуемое отношение сигнал/шум без кодирования; - требуемое отношение сигнал/шум при введении кодирования.

В табл. 5.1. приведены значения для рассмотренных кодов.

Таблица 5.1

	Без кодирования	Код (7.4)	Код (15.7)
	0 0	0,204 0,35	0,474 0,73

Приведенные здесь примеры демонстрируют порядок вычислений. Для полного анализа необходимо выполнить аналогичные расчеты для большого числа кодов.

На рис. 5.2. показаны результаты расчетов удельных затрат энергии и полосы для различных кодов БЧХ (2).

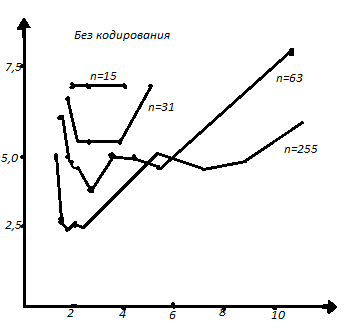
Рис. 5.2. Удельные затраты энергии и полосы использовании кодов БЧХ

В радиоканале символы передаются путем фазовой манипуляции,вероятность ошибки на 1 бит Р_b = 10^-5 . Параметр Для наглядности точки,соответствующие различные кодам,соединение прямыми линиями.Из этого рисунка видно, что наилучшие системы должны иметь избыточность,равную примерно 2. Но окончательный выбор можно произвести только с учетом сложности и надежности кодера и докодера. Практически в системах,использующих помехоустойчивые коды, достигается энергетический выигрыш 2-3 Дб.