4.2 Схемы кодирования для циклических кодов

Умножение на образующий полином

Наиболее простые схемы кодирования получается при реализации умножения на образующий полином кода.

Согласно определению циклического кода, кодовая комбинация U(x) принадлежит коду, если

U(x)=k(x)g(x),

где k(x) – полином, несущий информацию, т.е. его коэффициентами являются информационные символов; g(x)- образующий полином кода.

Таблица 4.2

№ такта	Состояния элементов схемы на рис. 4.9	№ такта	Состояния элементов схемы на рис. 4.10
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16	1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 1 1 0 0 0 1 1 0 0 0 1 1 1 1 0 1 1 0 1 0 0 1 0 1 1 1 1 0 0 1 1 1 1 1 1 1 1 0 1 1 1 0 0 1 1 0 0 0	1 2 3 4 5 6 7 8	1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 1 0 1 1 1 1 1 0 0 1 1 1 1 0 0 0

№ элемента задержки № Такта	1 2 3	Выходной символ Таблица 4.3
1 2 3 4 5 6 7	1 1 0 1 0 1 0 1 0 1 1 1 0 1 1 0 0 1 0 0 0	1 1 1 1 1 1 1

Однако при таком способе кодирования не происходит разделения информационных и проверочных символов.

Рассмотрим в качестве примера формирование кода. Хэмминга (7, 4) с образующим полиномом g(x)= .

Рис. 4.11. Схема умножения на полином

g(x)=

Схема умножения на g(x) показана на рис. 4.11. Пусть информационная последовательность равна 1 1 0 1, т. е. k(x)= . Тогда

U(x)=k(x)g(x)=

В табл. 4.3 записаны последовательные состояния элементов задержки и символы, формируемые на выходе схемы.

В течение первых четырех тактов проводятся вычисления, на последних трех тактах содержимое элементов задержки продвигается на выход.

Вычисление проверочных символов путем деления на g(x)

Чтобы получить систематический код, в котором разделены информационные и проверочные символы, надо произвести операции согласно соотношению (3.9). Практически для этого надо информационный полином 𝓀(x) разделить на g(x). Полученный в результате деления остаток дает проверочные символы.

Схема, реализующая эти операции, представлена на рис. 4.12, 𝑎. В течение первых 7 тактов происходит деление на g(x).Одновременно информационные символы поступают на выход (ключи К1, К2 в положении 1). В нашем случае число информационных символов равно 4. Остаток r(x) сформируются только по прошествии n=7тактов, поэтому имеет место пауза в 3 такта. После этого ключи К1 К2 должны быть переведены в положение 2 и проверочные символы поступят на выход. Состояния элементов задержки при кодировании последовательности 1101 приведены в табл. 4.4.

Таблица 4.4

№ элемента задержки № такта	1 2 3	Выходной символ
1 2 3 4 5 6 7 8 9 10	1 0 0 1 1 0 0 1 1 0 1 1 1 1 1 1 0 1 1 0 0 Остаток 0 1 0 0 0 1 0 0 0	1 1 0 1 } 0 0 1 Пауза

Получающиеся при тактом кодировании паузы технически неудобны. Их можно избежать несколькими способами. Наиболее очевидный способ представлен на рис. 4.12,б. Эта схема практически повторяет схему на рис. 4.12,𝑎, но информационные символы поступают на выход с задержкой на r тактов, в результате ликвидируется пауза в середине кодовой группы.

Таблица 4.5

№ такта	Элементы задержки			Ключи			Выходные символы
	1	2	3	1		2
1 2 3 4 5 6 7	1 1 0 1 0 1 1 0 0 1 0 0 0 1 0 0 0 1 0 0 0			1	1		1 1 0 1 0 0 1
				2	2

На рис. 4.12,в представлена схема кодирования, которая находит практическое применение. Для того чтобы избежать задержки на r тактов, информационная последовательность

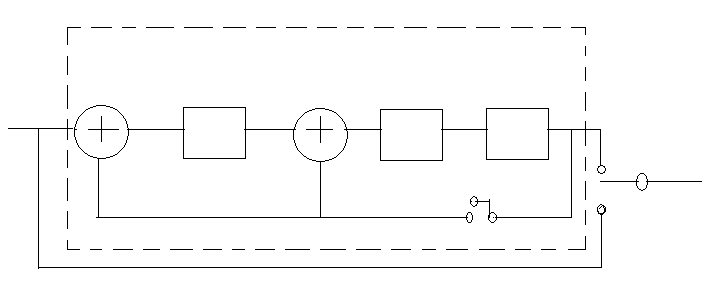
Схема деления на g(x)

2

1

K2

2 K1

1

Выход

Вход

𝑎)

б)

Деление на g(x)

Задержка на r тактов

Выход

2

1

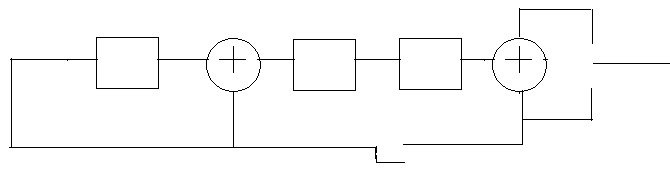
В)

2

1

К2

1

2

К1

Выход

г)

Рис. 4.12. Схемы формирования кода Хэмминга (7.4)

вводится сразу в «конец» схемы, что эквивалентно умножению на . В табл. 4.5 приведены состояния элементов схемы при кодировании последовательности 1101.

Вычисление проверочных символов с помощью полинома h(x)

Проверочные символы можно вычислять, использую полином h(x) или, что то же самое, проверочную матрицу Н.

Строки проверочной матрицы указывают, какие символы должны участвовать в данной проверке.

Например, для рассматриваемого нами кода Хэмминга (7.4) проверочная матрица Н имеет вид

Н=

Ей соответствует кодирующая схема на рис. 4.12,г

Информационные символы вводится в элементы задержки параллельно. Затем в течение 3 тактов вычисляются проверочные символы путем сложения содержимого 1, 2 и 3-го элементов задержки (см. первую строку матрицы Н). Напомним, что строки матрицы Н могут быть получены циклической перестановкой первой строки. Эта цикличность и отражена в записи результата сложения в последний (четвертый) элемент задержки.

В табл. 4.6 записаны последовательные состояния элементов задержки схемы на 4.12,г как в общем виде, так и при кодировании последовательнос-ти 1101.

В общем виде кодирующая схема, использующая полином h(x)= + показана на рис. 4.13.

Рис. 4.13. Кодирующая схема с использованиям проверочного полинома h(x)

Кодирующие схемы, строящиеся на базе образующих и проверочных полиномов, совершенно равноправны. Однако для кодов с большой избыточностью (𝓀 удобнее пользоваться схемами, как на рис. 4.13, поскольку они содержат меньшее число элементов задержки. Если же 𝓀 то меньшее число элементов имеют схемы, использующие полином g(x). В качестве примера на рис. 4.14 показаны два варианта кодирующих схем для кода БЧХ (15,7) с образующим полиномом

g(x)=

№ элемента задержки № такта	1	2	3	4
1
	1	1	0	1
2
	1	0	1	0
3
	0	1	0	0
4				(
	1	0	0	0
5
	0	0	1
6
	1	0
7
	1

и соответствующим ему проверочным полиномом

h (x)=