МИНИСТЕРСТВО ВЫСШЕГО И СРЕДНЕГО СПЕЦИАЛЬНОГО ОБРАЗОВАНИЯ СССР
МОСКОВСКИЙ ордена ЛЕНИНА и ордена ОКТЯБРЬСКОЙ РЕВОЛЮЦИИ
ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТ
Е.Е.ЛАЗАРЕВ
ПОМЕХОУСТОЙЧИВЫЕ КОДЫ В СИСТЕМАХ ПЕРЕДАЧИ ЦИФРОВОЙ ИНФОРМАЦИИ
МИНИСТЕРСТВО ВЫСШЕГО И СРЕДНЕГО СПЕЦИАЛЬНОГО ОБРАЗОВАНИЯ СССР
МОСКОВСКИЙ ордена ЛЕНИНА и ордена ОКТЯБРЬСКОЙ РЕВОЛЮЦИИ
ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТ
Е.Е.ЛАЗАРЕВ
Утверждено
Учебно- математическим управлением МЭИ
в качестве учебного пособия
для студентов
УЧЕБНОЕ ПОСОБИЕ
По курсу
СИСТЕМЫ ПЕРЕДАЧИ ИНФОРМАЦИИ
ПОМЕХОУСТОЙЧИВЫЕ КОДЫ В СИСТЕМАХ ПЕРЕДАЧИ ЦИФРОВОЙ ИНФОРМАЦИИ
Редактор П.И. Пенин
Москва 1980
Глава 1
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ КОДИРОВАНИЯ
Введение
Развитие систем передачи дискретной информации потребовало освоения способов приема и передачи с очень высокой степенью достоверности. При автоматизированной обработке информации с использованием ЦВМ предъявляются повышенные требования к качеству работы канала связи. Возможны два пути решения этой проблемы: во- первых: уменьшать вероятность ошибок в высокочастотной части системы связи, но при этом возрастают затраты энергии или уменьшается скорость передачи информации; во- вторых, использовать какой- либо код, исправляющий или обнаруживающий ошибки на выходе демодулятора.
Основы теории кодирования были заложены К.Шенноном, который определил понятие количества информации и пропускной способности и сформулировал теорему о кодировании. Однако эта теория говорила только о потенциальных возможностях систем передачи информации. Значительные успехи в разработке кодов, допускающих несложную практическую реализацию, были достигнуты позднее.
Одновременно имел место огромный скачок в развитии электронных устройств на интегральных схемах. Эти достижения привели к тому, что в настоящее время использование кодов, исправляющих ошибки, стало практически осуществимым в системах передачи дискретной информации.
Задачей этого учебного пособия является объяснение логики построения кодов и процедур декодирования, ознакомление с наиболее распространенными кодами, разъяснение возможностей кодов и целесообразности их применения.
Структура системы передачи цифровой информации
При анализе системы передачи цифровой информации будем предполагать, что каким- то образом уже произведено первичное кодирование сообщений, подлежащих передаче. Структурная схема такой линии связи представлена на рис.1.1.
В
дальнейшем рассматривается только
такой случай, когда источник дискретной
информации вырабатывает последовательность
двоичных символов
,
например нули и единицы. Кодирующее
устройство преобразует эту информационную
Источник дискрет информ. |
|
Кодер |
|
Модулятор передатчик |
|
Среда распрост. |
|
Приемник демодулятор |
|
Декодер |
|
Получатель |
|
|
|
|
|
|
Рис. 1.1. Структурная схема цифровой линии связи
Последовательность в новую последовательность двоичных символов, обладающую некоторой избыточностью для повышения помехоустойчивости. Отметим здесь, что мы не будем рассматривать кодеры, осуществляющие статистический анализ поступающей информации и статистическое кодирование.
Последовательностью,
сформированной на выходе кодера {
},
производится манипуляция какого- либо
параметра сигнала- переносчика. На
приемной стороне выполняются обратные
операции: демодуляция и декодирование.
В процессе распространения сигнал подвергается искажениям, к нему добавляются помехи. В результате на выходе демодулятора получится последовательность { }, которая может отличаться от передаваемой. Возникнут ошибки, представляющие в нашем случае замену некоторых единиц на нули и наоборот. Задача декодера – исправить ( или обнаружить) такие ошибки.
Разбирая работу кодера – декодера, можно часть схемы от входа модулятора до выхода демодулятора характеризовать только вероятностями перехода одного символа в другой. Эти переходы показаны на рис. 1.2.
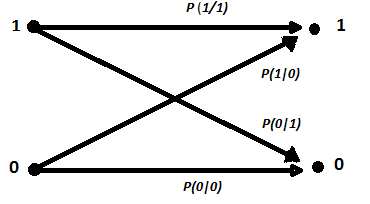
Рис. 1.2. Модель двоичного симметричного канала
Как правило, выполняется равенство вероятностей переходов [1]: P(0|0) = P(1|1) и P(1|0) = P(0|1)/. Такой канал называется симметричным.
В двоичном симметричном канале достаточно знать единственную характеристику – вероятность ошибки.
,
(1.1) где
и
-
априорные вероятности появления единицы
и нуля в последовательности
};
P(1)=
P(0)=
0,5