3.1. Теоретическое введение

Скорость химической коррозии металлов определяется или скоростью самого кристаллохимического процесса образования пленки, или скоростью встречной двусторонней диффузии через пленку действующего реагента и металла.

Линейный закон окисления металла

Если при окислении металлов протекают процессы, не приводя­щие к образованию сплошной оксидной пленки, что возможно при наличии возгоняющихся в данных условиях оксидов, рыхлых пористых или растрескивающихся оксидов, скорость коррозии может контроли­роваться, либо скоростью химической реакции кислорода и металла, либо скоростью процессов, вызывающих нарушение целостности ок­сидной пленки. В предельном случае, когда продукты взаимодейст­вия не защищают металл от окислительной среды, скорость окисления будет определяться также скоростью химической реакции. Та­ким образом, максимально возможная скорость химической коррозии металла - это скорость химической реакции взаимодействия метал­ла и кислорода.

Так как в рассмотренных случаях пленка практически не пре­пятствует окислению металла ни на одном этапе, то скорость окис­ления должна оставаться постоянной в течение всего процесса окис­ления.

dh / dτ = K₁ (3.1)

где K₁ - константа скорости роста оксидной пленки, зависящая от концентрации кислорода в газовой фазе и давления газа (с увеличением этих параметров она также увеличивается); h - толщина пленки; τ - время.

Интегрирование уравнения (3.1) дает возможность найти закон роста пленки во времени:

h = K₁τ+С₁ (3.2)

этот закон называется линейным. С₁ - постоянная интегриро­вания, равная толщине пленки в начальный момент: С₁ = h₀ при τ = 0. Если h₀ =0 (при τ = 0), то С = 0 и уравнение (3.2) принимает вид:

h = K₁ ∙ τ (3.3)

Для нахождения константы K₁ в случае линейного закона строится график (см. рисунок 1) в координатах h = f(τ), представляющий собой прямую линию, тангенс угла наклона которой равен K₁(tgα = K₁).

Риcунок – 1 Законы роcта пленок на металлах: линейный,

параболический и логарифмический законы в координатах h - τ

Параболический закон окисления металла

Параболическое окисление наблюдается в тех случаях, когда на поверхности металла образуется сплошная, плотно прилегающая к его поверхности оксидная пленка. Закономерности роста такой пленки определяются закономерностью перемещения в ней частиц окислителя и металла. Такими частицами в общем случае могут быть катионы, анионы и электроны. Механизм перемещения частиц в плен­ке представляет собой диффузию. Независимо от места расположения зоны роста пленки (со стороны газовой среды, металла или внутри пленки), кинетическая закономерность окисления одинакова - она выражается уравнением квадратичной параболы. Уравнение роста ок­сидной пленки в этом случае имеет вид:

h² = K₂ τ . (3.4)

Параболический закон окисления имеет место при взаимодействии с кислородом многих металлов. Однако наиболее часто на практике встречается закономерность окисления, описыва­емая степенным законом роста (см. рисунок 1)

, (3.5)

где К₃ - константа скорости окисления; n - показатель сте­пени, причем 1< n ≤2 или n >2; иногда окисление описы­вается кубическим уравнением.

Если кривая имеет вид зависимости (3.5), то для подтверждения справедливости установленной зависимости, на­хождения показателя n и константы K₃ кривую спрямляют, строят график (см. рисунок 2) в координатах lg h = f(lg τ), кото­рый для параболической зависимости должен дать прямую

lgh = 1/n lg K₃+1/n lg τ ,

где 1/n = tg α, lgK₃/n - отрезок, отсекаемый на оси ординат (при lg τ = 0).

Рисунок 2 – График для определения параметров " n " и "К₃" в случае параболического закона роста пленок

Значение показателя n и константы К₃ находят из графика: 1) n = ctg α , 2) 1/n lg K₃ = lgh при lg τ = 0 или

lg K₃ = n lgh, откуда при известном значении n рассчитывается значение постоянной K₃.

Возможны случаи, когда первоначально процесс окисления металлического материала может протекать с образованием защитной оксидной пленки с показателем n ≥ 2 в кинетическом уравнении (3.5), а с увеличением длительности изотермической выдержки происходит разрушение (растрескивание, осыпание) оксидной пленки, и n становится ≤ 1.

Изменение в структуре пленки по мере ее роста может привес­ти к изменению величины n и К₃ в уравнении (3.5). Смена законов в процессе окисления металлов характерна для так назы­ваемого паралинейного закона (в начальный период - параболичес­кий, затем - линейный закон). Переход к линейному закону соответ­ствует установлению равенства скоростей образования окисла (во внутренней части) и разрушения его (снаружи).

Для описания зависимости толщины пленки от времени (1<n<2), в общем виде может быть использовано уравнение, предложенное Эвансом

K₁h²+K₂h = K₁K₂ τ (3.6)

Для нахождения неизвестных K₁ и K₂ уравнение преобразуют к виду: τ/h =1/K₁+h/K₂ и строят график в координатах τ/h = f(h), который должен дать прямую линию (см. рисунок 3). Тангенс угла наклона этой линии tgα = 1/K₂ , а 1/K₁ - отрезок, отсекаемый на оси ординат (при h = 0).

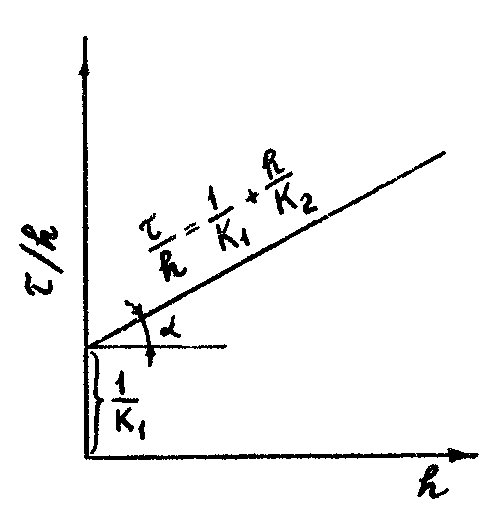
Рисунок 3 – Параболический закон в координатах (τ/h)–h