
Элементы комбинаторики
§1. Декартово произведение двух множеств
Рассмотрим
пример. Число 35 записывается с помощью
двух цифр 3 и 5. Эти цифры следует записывать
в определенном порядке: сначала 3, а
потом 5. Если их переставить, получится
другое число 53. Говорят, что
![]() — упорядоченная
пара чисел.
Упорядоченную пару чисел
— упорядоченная
пара чисел.
Упорядоченную пару чисел
![]() и
и
![]() будем записывать следующим образом:
будем записывать следующим образом:
![]() .
В число 44 входят две одинаковые цифры.
Они образуют упорядоченную пару
.
В число 44 входят две одинаковые цифры.
Они образуют упорядоченную пару
![]() .
Таким образом, в упорядоченных парах
числа могут повторяться.
.
Таким образом, в упорядоченных парах
числа могут повторяться.
Упорядоченные
пары можно составлять не только из
чисел, но и из элементов любых множеств.
Пусть задано множество
![]() и пусть
и
— элементы этого множества (при этом
может случиться, что
и пусть
и
— элементы этого множества (при этом
может случиться, что
![]() ).
Назовем
).
Назовем
![]() упорядоченной
парой, а
упорядоченной
парой, а
![]() и
и
![]() — компонентами
или координатами
этой пары.
— компонентами
или координатами
этой пары.
Пары
![]() и
и
![]() считаются совпадающими
в том и только
том случае, когда
считаются совпадающими
в том и только
том случае, когда
![]() и
и
![]() .
Поэтому, если
.
Поэтому, если
![]() ,
то пары
и
,
то пары
и
![]() различны.
различны.
Например,
из букв множества
![]() можно составить девять упорядоченных
пар:
можно составить девять упорядоченных
пар:
![]() .
Примером упорядоченной пары натуральных
чисел может служить пара, составленная
из числителя и знаменателя дроби —
вместо того, чтобы писать
.
Примером упорядоченной пары натуральных
чисел может служить пара, составленная
из числителя и знаменателя дроби —
вместо того, чтобы писать
![]() ,
можно записать
,
можно записать
![]() .
При перестановке чисел 3 и 5 получается
иная дробь
.
При перестановке чисел 3 и 5 получается
иная дробь
![]() .
.
Еще
более общее понятие упорядоченной пары
получается, если брать ее компоненты
из различных множеств. Например,
компоненту
![]() из множества
из множества
![]() ,
а —
из множества
,
а —
из множества
![]() .
Пусть, например, заданы два множества
.
Пусть, например, заданы два множества
![]() и
и
![]() .
Образуем из элементов этих множеств
пары так, чтобы первая компонента пары
принадлежала множеству
,
а вторая множеству
.
Все эти пары
составляют множество:
.
Образуем из элементов этих множеств
пары так, чтобы первая компонента пары
принадлежала множеству
,
а вторая множеству
.
Все эти пары
составляют множество:
![]() ,
которое является декартовым произведением
множеств
и
,
обозначают
,
которое является декартовым произведением
множеств
и
,
обозначают
![]() .
.
Определение.
Декартовым произведением множеств
и
наз. множество
,
элементами которого являются все пары
такие, что
![]() ,
,
![]() ,
т. е.
,
т. е.
![]() .
.![]()
Если
множества
и
![]() совпадают,
т.е.
совпадают,
т.е.
![]() ,
то множество
,
то множество
![]() состоит из всех пар
таких, что
состоит из всех пар
таких, что
![]() ,
,
![]() .
.
Полагают,
что
![]() для любого множества
.
для любого множества
.
Декартово произведение множеств, вообще говоря, не обладает ни свойством коммутативности, ни свойством ассоциативности, т. е.:
если
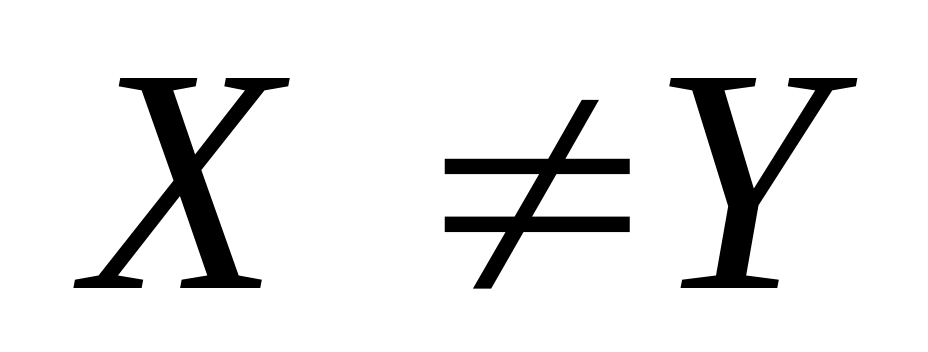 ,
то
,
то
 ;
;если ни одно из множеств
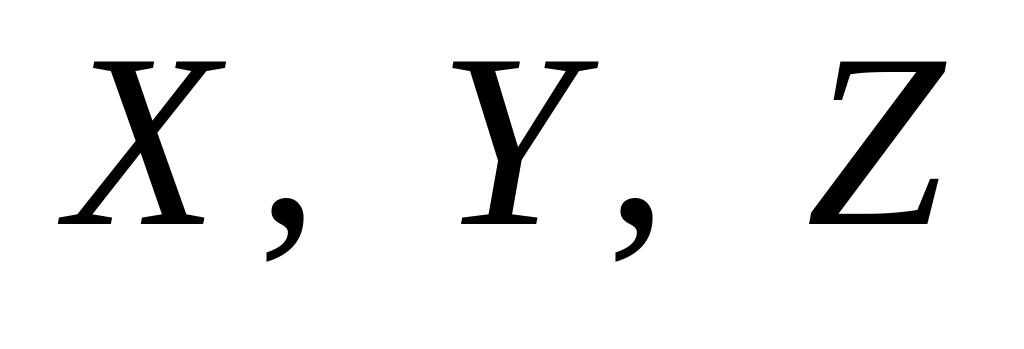 не пусто, то
не пусто, то
 .
.
Действительно,
элементами множества
являются пары
такие, что
и
,
а элементами
множества
![]() — пары
— пары
![]() ,
где
и
.
Но, при
пары
и
различны. Следовательно, если
,
то множества
и
различны.
,
где
и
.
Но, при
пары
и
различны. Следовательно, если
,
то множества
и
различны.
Элементы декартова
произведения двух конечных множеств
удобно располагать в виде таблицы, где
по вертикали располагают элементы
множества
,
по горизонтали — элементы множества
,
а элементы множества
пишут на пересечениях соответствующих
строк и столбцов. Так, на таблице,
приведенной ниже, изображены элементы
декартова произведения множеств
![]() и
и
![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
Задания для практических занятий и самостоятельного решения.
1.
Выпишите три упорядоченные пары
действительных чисел, являющихся
решением уравнения
![]() .
.
2.
Даны два множества
,
![]() .
Запишите элементы множества
.
Запишите элементы множества
![]() .
.
3.
Даны три множества
![]() ,
,
![]() ,
,
![]() .
Запишите элементы множеств
.
Запишите элементы множеств
![]() .
.
4.
Докажите
справедливость равенства:
![]() .
.
5.
Верно ли
равенство:
![]() ,
если
,
если
![]() ?
?
6.
Составьте
все дроби, числитель и знаменатель
которых – разные однозначные числа из
множества
![]() .
Сколько дробей получилось?
.
Сколько дробей получилось?
