Тема 11 Зубчатые передачи. (1/-/- час)

План лекции:

1. Общие сведения

2. Характер и причины отказов зубчатых передач

3. Цилиндрические зубчатые передачи

3.1. Силы в зацеплении

3.2. Особенности геометрии и условий работы косозубых зубчатых передач

3.3. Понятия об эквивалентном колесе

4. Конические зубчатые передачи

4.1. Осевая форма зуба

4.2. Основные геометрические соотношения

4.3. Эквивалентное колесо

4.4. Силы в зацеплении

В зубчатой передаче движение передают с помощью зацепления пары зубчатых колес. Меньшее зубчатое колесо принято называть шестерней, большее — колесом. Термин "зубчатое колесо" относят как к шестерне, так и к колесу.

Достоинства зубчатых передач:

1. Относительно малые размеры и масса зубчатых колес при высокой нагрузочной способности и надежности.

2. Высокий КПД (97 – 98 %).

3. Возможность использования зубчатых передач в большом диапазоне нагрузок (окружные силы от близких к нулю в приборных механизмах до ~ 1000 кН в приводах прокатных станов).

4. Возможность применения в широком диапазоне скоростей (окружные скорости от близких к нулю в системах перемещения телескопов до 250 м/с в приводе несущего винта вертолета).

5. Сравнительно малые нагрузки на валы и подшипники.

6. Постоянство среднего значения передаточного числа.

7. Простота обслуживания.

Недостатки:

1. Необходимость высокой точности изготовления и монтажа.

2. Шум при работе передачи. Шум обусловлен переменным значением мгновенного передаточного числа в пределах одного оборота.

Зубья колес получают нарезанием или накатыванием

Зубчатые передачи применяют в широком диапазоне областей и условий работы: часы и приборы, коробки передач автомобилей, тракторов, других транспортных и дорожно-строительных машин, механизмы подъема и поворота кранов, коробки скоростей станков, приводы прокатных станов, конвейеров и многое другое.

Зубчатые передачи подразделяют по геометрическим параметрам на цилиндрические с внешним или внутренним зацеплением и конические.

Цилиндрические передачи с внешним зацеплением (рис. 35). Шестерня в понижающей передаче является ведущим элементом и всем ее параметрам присваивают индекс 1. Например, частота вращения n₁, мин^–1, число зубьев z₁. Параметры ведомого элемента пары — колеса имеют индекс 2: n_2, z₂.

Линии пересечения боковых поверхностей зубьев с любой круговой цилиндрической поверхностью, соосной с начальной, называют линиями зубьев. Если линии зубьев параллельны оси зубчатого колеса, то его называют прямозубым (рис. 35,а). Если эти линии винтовые постоянного шага, то зубчатое колесо называют косозубым (рис. 35,б). С увеличением угла β наклона зуба повышается нагрузочная способность передачи, но возрастает осевая сила, действующая на валы и опоры. Обычно β = 8...18°.

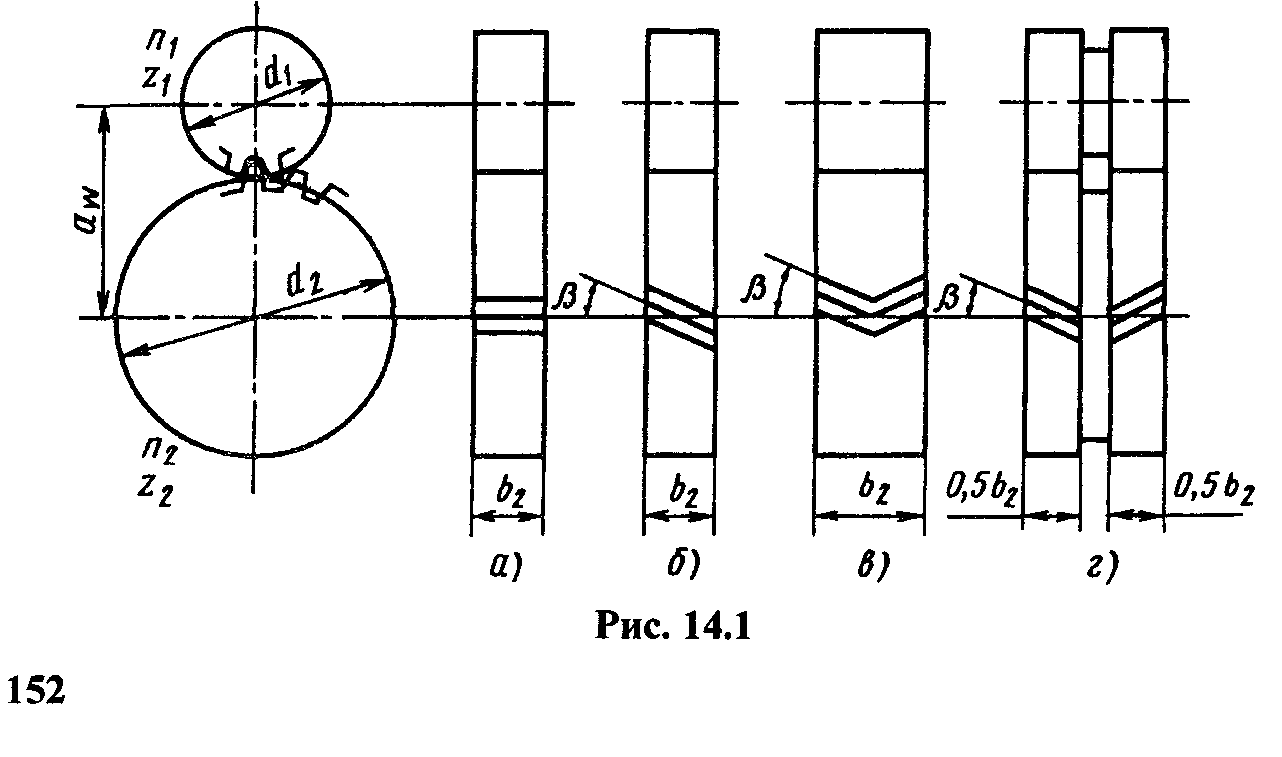
Рисунок 35 – Цилиндрические передачи с внешним зацеплением

Разновидность косозубых зубчатых колес — шевронные колеса: без канавки (рис. 35,в) и с канавкой для выхода инструмента (рис. 35,г). Вследствие противоположного направления зубьев на полушевронах осевые силы взаимно уравновешены на колесе и не нагружают опоры. Обычно β = 25...40°.

Конические зубчатые передачи передают механическую энергию между валами с пересекающимися осями. Обычно Σ = 90° (рис. 40,а). Зацепление конических зубчатых колес можно рассматривать как качение делительных круговых конусов шестерни и колеса. Основные характеристики: углы делительных конусов δ₁ и δ ₂, внешнее конусное расстояние R_e.

Линии пересечения боковых поверхностей зубьев с делительной конической поверхностью называют линиями зубьев. В зависимости от формы линии зуба различают передачи с прямыми зубьями (рис. 40,б), у которых линии зубьев проходят через вершину делительного конуса, и с круговыми зубьями (рис. 40,в), линии зубьев которых являются дугами окружности d₀.

Конические колеса с круговыми зубьями характеризуют наклоном линии зуба в среднем сечении по ширине зубчатого венца. Угол β_n наклона — острый угол между касательной в данной точке к линии зуба и образующей делительного конуса (рис. 40,в).

Разновидностью конических передач являются гипоидные передачи, у которых оси вращения зубчатых колес не пересекаются, а перекрещиваются.

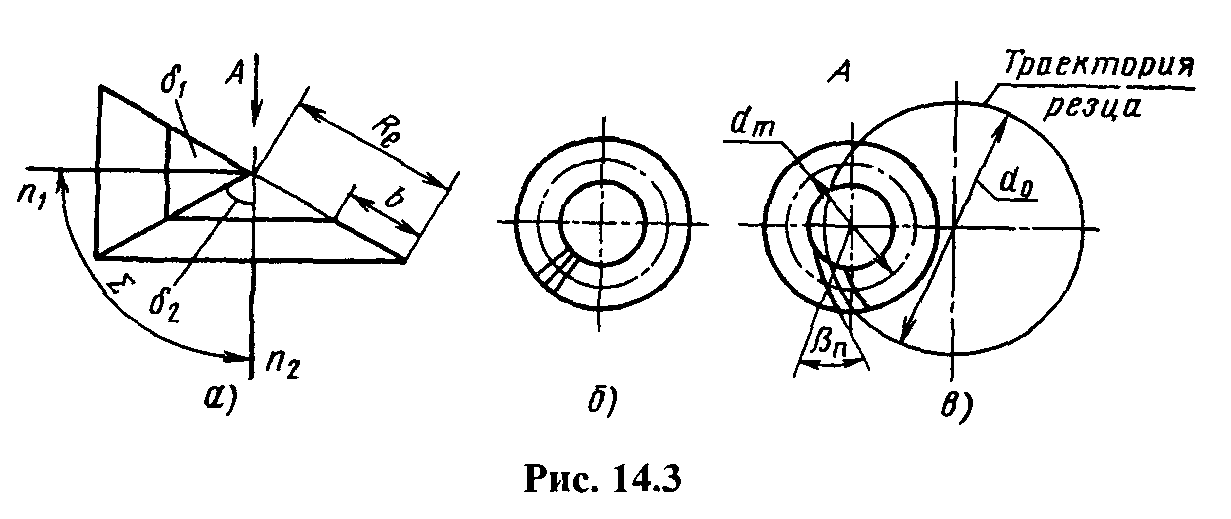
Рисунок 40 –Конические зубчатые передачи

Геометрия конических зубчатых передач представлена на рис.41.

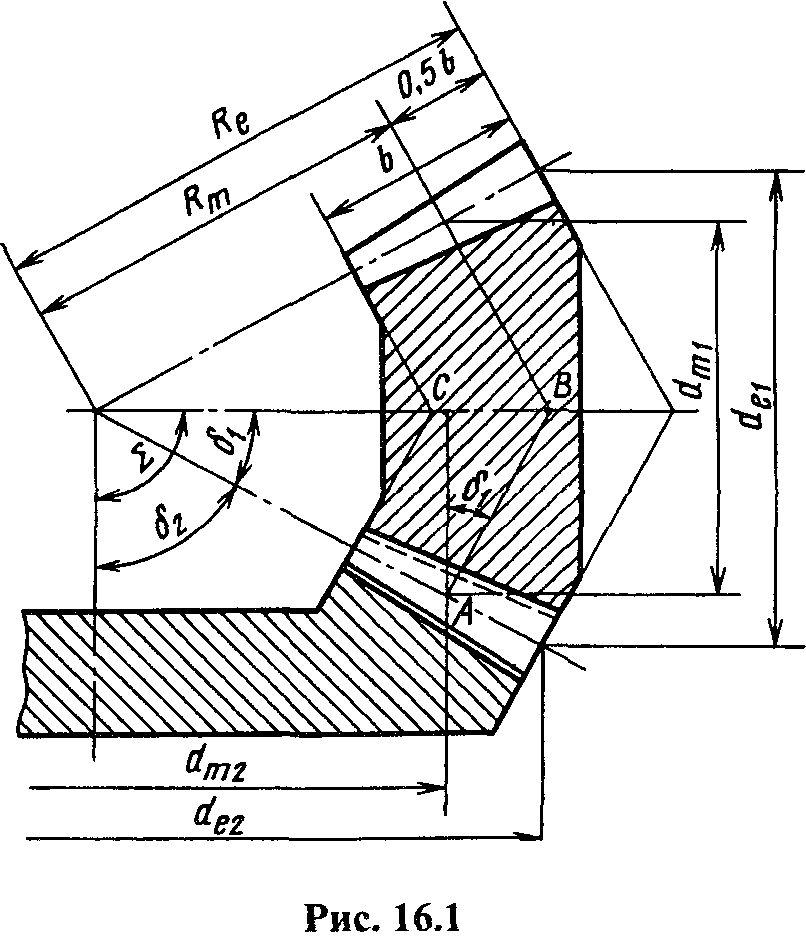
Рисунок 41 – Геометрия конических зубчатых колес

Конические зубчатые передачи необходимо регулировать, добиваясь совпадения вершин делительных конусов колес.

Угол Σ между осями зубчатых колес равен сумме углов делительных конусов (рис. 18.1):

, (61)

Достоинство конических передач – возможность передачи механической энергии между валами с пересекающимися осями.

Недостатками являются необходимость регулирования передачи (вершины делительных конусов должны совпадать), а также меньшая нагрузочная способность и большая сложность изготовления по сравнению с цилиндрическими передачами.

Внешние и внутренние торцы на конических зубчатых колесах формируют внешними и внутренними дополнительными конусами, образующие которых перпендикулярны образующей делительного конуса. Средний дополнительный конус расположен на равном расстоянии от внешнего и внутреннего дополнительных конусов.

Ширина b венца зубчатого колеса ограничена двумя дополнительными конусами – внешним и внутренним.

Длину отрезка образующей делительного конуса от его вершины до внешнего торца называют внешним конусным расстоянием R_e, до середины ширины зубчатого венца – средним конусным расстоянием R_m (рис. 41).

Пересечения делительных конусов с дополнительными конусами определяют диаметры делительных окружностей конического зубчатого колеса. Различают внешний d_e, внутренний d , средний d_m делительные диаметры.

Передаточное число. Согласно рис. 41 передаточное число:

, (62)

где d_e1, d_e2, d_m1, d_m2 и , – соответственно внешние, средние делительные диаметры и углы делительных конусов шестерни и колеса.

Для конической прямозубой передачи рекомендуют и=2...3; при колесах с круговыми зубьями и до 6,3.

Осевая форма зуба. Зубья конических колес в зависимости от изменения размеров их нормальных сечений по длине выполняют трех осевых форм (рис. 42):

• осевая форма I– нормально понижающиеся зубья (рис. 42,а). Вершины конусов делительного и впадин совпадают, высота ножки зуба пропорциональна конусному расстоянию. Применяют для прямых зубьев, а также ограниченно для круговых при т ≥ 2мм и

, (63)

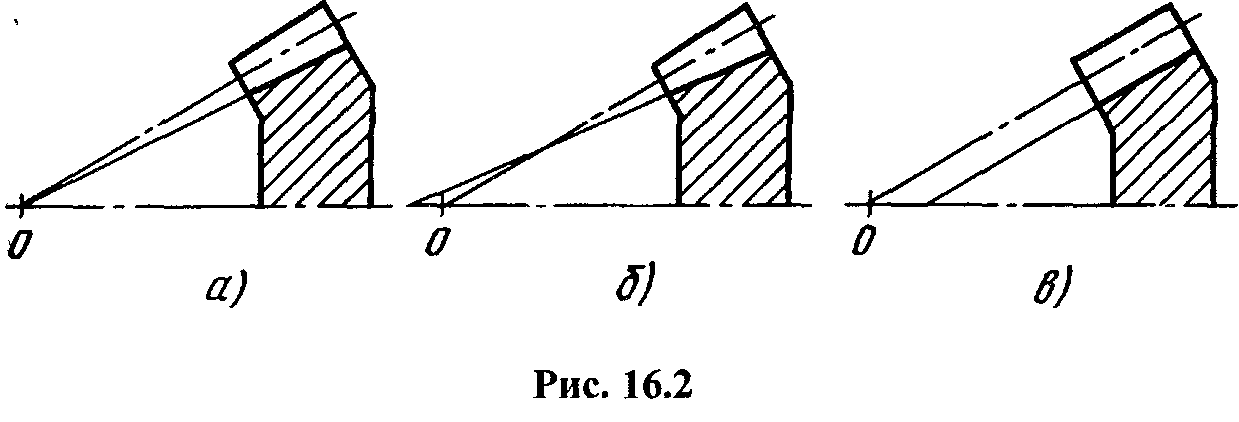
Рисунок 42 – Осевые формы зуба

• осевая форма II– нормально сужающиеся зубья (рис. 42,б). Вершина конуса впадин расположена так, что ширина дна впадины колеса постоянна, а толщина зуба по делительному конусу пропорциональна конусному расстоянию. Эта форма обеспечивает оптимальную прочность на изгиб во всех сечениях, позволяет одним инструментом обрабатывать сразу обе поверхности зубьев колеса, что повышает производительность при нарезании зубчатых колес. Является основной для колес с круговыми зубьями. Применяют в массовом производстве;

• осевая форма III – равновысокие зубья (рис. 42,в). Образующие конусов делительного, впадин и вершин параллельны. Высота зубьев постоянна по всей длине. Применяют для неортогональных передач с межосевым углом Σ<40° и круговыми зубьями при

, (64)

Основные геометрические соотношения. В конических зубчатых колесах с осевыми формами I и II высота зуба, а следовательно, и модуль зацепления увеличиваются от внутреннего к внешнему дополнительному конусу (рис. 41, 42). Для удобства измерения размеры конических колес принято определять по внешнему торцу зуба.

Максимальный модуль зубьев – внешний окружной модуль т_te –получают на внешнем торце колеса.

Ниже приведены основные геометрические соотношения для конических зубчатых передач (рис. 41).

Внешнее конусное расстояние:

, (65)

Внешние делительные диаметры шестерни и колеса:

, (66)

Ширина зубчатого венца:

, (67)

Для большинства конических передач коэффициент ширины зубчатого венца .

Тогда:

, (68)

Среднее конусное расстояние:

, (69)

Из условия подобия (рис. 18.1) следует:

, (70)

Тогда средний делительный диаметр шестерни:

, (71)

Модуль окружной в среднем сечении:

, (72)

Модуль нормальный в среднем сечении для кругового зуба ( =35°):

, (73)

Углы делительных конусов:

, (74)

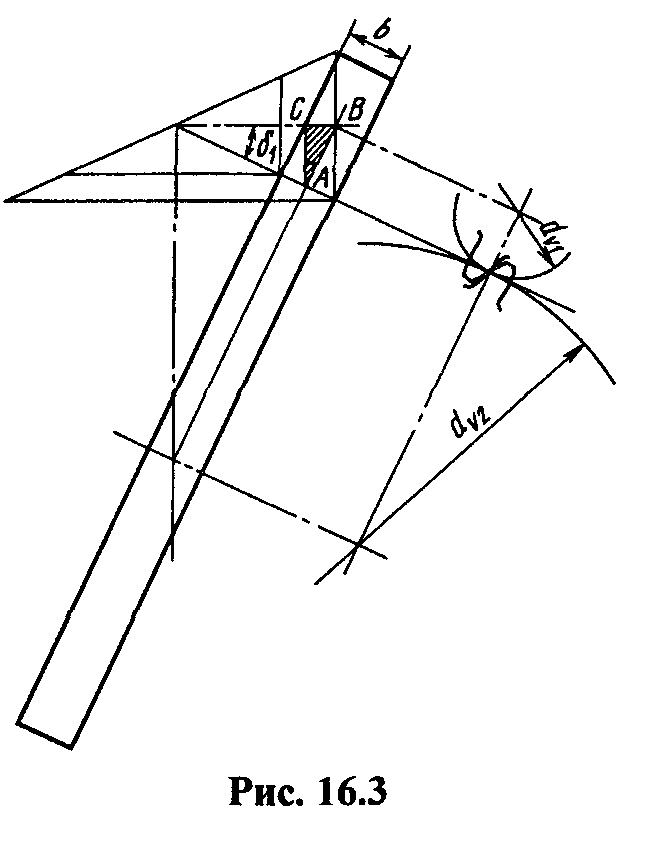
Рисунок 43 – Эквивалентное колесо

Для конических зубчатых колес с прямыми зубьями в качестве расчетного принимают внешний окружной модуль m_te, для конических зубчатых колес с круговыми зубьями – средний нормальный модуль т_п в середине зубчатого венца.