
- •Дихтярь м.Б., доцент, канд. Физ.-мат. Наук
- •8. Найдите все натуральные числа, последняя десятичная цифра которых 0 и, которые имеют 15 натуральных делителя (включая единицу и само число).
- •9. Найдите все натуральные числа, которые делятся на 42 и имеют ровно 42 натуральных делителей (включая единицу и само число).
- •Упражнения
Подготовка к ЕГЭ.
Решение одного из типов задач в задании С 6.
Дихтярь м.Б., доцент, канд. Физ.-мат. Наук
Рассмотрим
некоторые задачи ЕГЭ, в которых
используется следующее. Любое натуральное
число
![]() можно единственным способом представить
в виде
можно единственным способом представить
в виде
![]() ,
где
,
где
![]() – простые числа,
– простые числа,
![]()
![]() – натуральные числа.
– натуральные числа.
Число
делителей числа
,
где
– простые числа,
– натуральные числа, включая единицу
и число n,
равно произведению
![]() .
.
Доказательство.
Любой делитель числа
![]() можно представить в виде
можно представить в виде
![]() где
где
![]() принимают независимо друг от друга
значения
принимают независимо друг от друга
значения
![]()
По правилу произведения (комбинаторика) число делителей числа n, включая единицу и число n, равно произведению .
Равенство называется разложением натурального числа n на простые множители.
Найдите число делителей числа 12!, включая единицу и само число.
Решение. Разложим число 12! на простые множители. Имеем
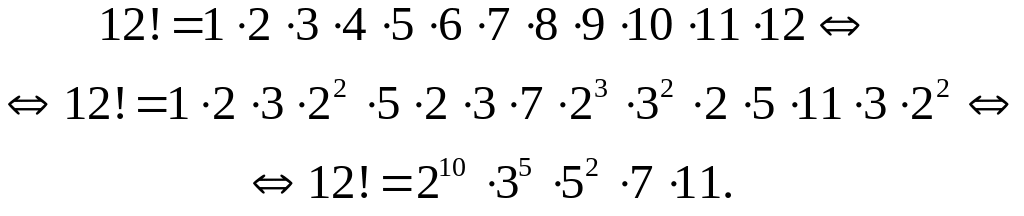
Так
как
![]() то число делителей числа 12!, включая
единицу и само число 12!, равно произведению
то число делителей числа 12!, включая
единицу и само число 12!, равно произведению
![]()
Ответ.792.
Формулы, используемые при решении задач
1.
Сумма
![]() первых
первых
![]() членов
геометрической прогрессии
членов
геометрической прогрессии
![]() ,
со знаменателем
,
со знаменателем
![]() равна
равна
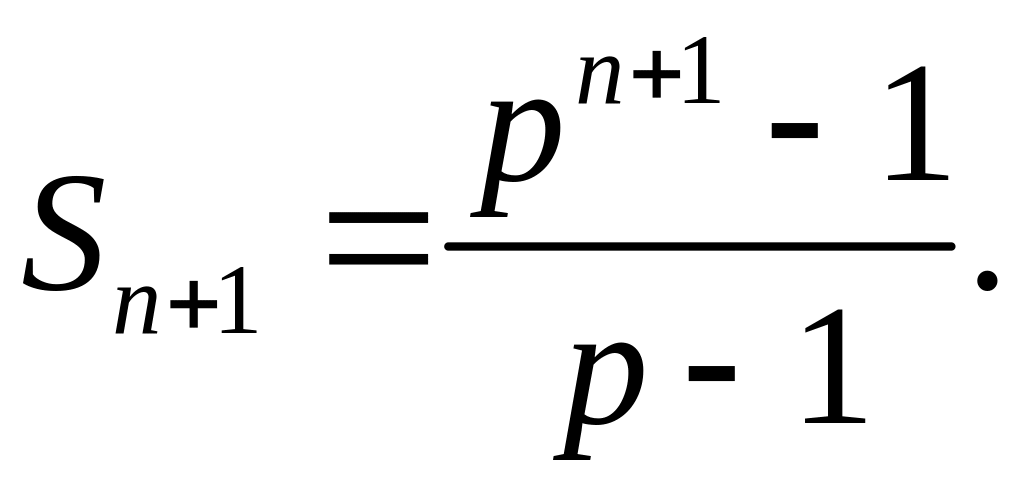 (1)
(1)
2.
![]() (2)
(2)
Доказательство.

Формула (2) доказана.
3.
![]()
![]() (3)
(3)
Доказательство.
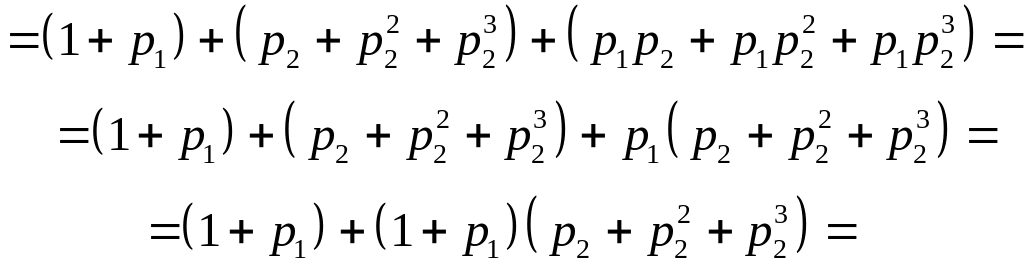
![]()
Формула (3) доказана.
4.
![]()
![]() (4)
(4)
Доказательство.

![]()
Формула (4) доказана.
5.
![]()
![]() (5)
(5)
Доказательство.
![]()

Формула (5) доказана.
Задачи
1. У натурального числа n ровно 6 натуральных делителей (включая единицу и само число). Сумма этих делителей равна 798. Найдите все такие числа.
Решение.
Пусть искомое натуральное число
представлено в виде
,
где
– простые числа,
–
натуральные числа. Число делителей
числа n,
включая единицу и число n,
равно
![]() .
Рассмотрим два случая.
.
Рассмотрим два случая.
1.
Из условия задачи, имеем
![]()
1)
Так как
![]() и
и
![]()
![]() – натуральные, не равные единицы числа,
то
– натуральные, не равные единицы числа,
то
![]() и
и
![]() .
Итак,
.
Итак,
![]() и
и
![]()
2)
Найдём
![]() .
.
Делителями
числа n
являются
числа:
![]() Воспользуемся формулой (1)
Воспользуемся формулой (1)

По
условию задачи

Так
как
простое число и
![]() ,
то
,
то
![]() .
Простое число
может принимать хотя бы одно из значений:
2; 3. Проверкой убеждаемся, что ни
.
Простое число
может принимать хотя бы одно из значений:
2; 3. Проверкой убеждаемся, что ни
![]() ни
ни
![]() не удовлетворяют уравнению
не удовлетворяют уравнению
![]()
Искомое число не может принимать вид
2.
Из условия задачи имеем
![]() .
.
1)
Так как
![]() и
и
![]() – натуральные, не равные единицы числа,
то
– натуральные, не равные единицы числа,
то
![]() и
и
![]()
Найдём
![]() и
и
![]() .
Так как
.
Так как
![]() и
и
![]() – натуральные не равные единицы числа,
то
(или
)
может принимать значение, равное 1 или
2. Пусть
– натуральные не равные единицы числа,
то
(или
)
может принимать значение, равное 1 или
2. Пусть
![]() и
и
![]() .
Тогда
.
Тогда
![]()
2)
Найдём
и
![]() .
.
Делителями
числа n
являются
числа:
![]() Воспользуемся формулой (2)
Воспользуемся формулой (2)
![]()
Из
условия задачи имеем
![]() (6)
(6)
3) Оценим . Рассмотрим (6).
Так как и простые числа, число 798 чётное, не кратно 4 и
![]() нечётное
число, то из (6) следует, что
нечётное
число, то из (6) следует, что
![]() и
и
![]() Тогда
Тогда
![]() .
.
Так
как
![]() ,
то
,
то
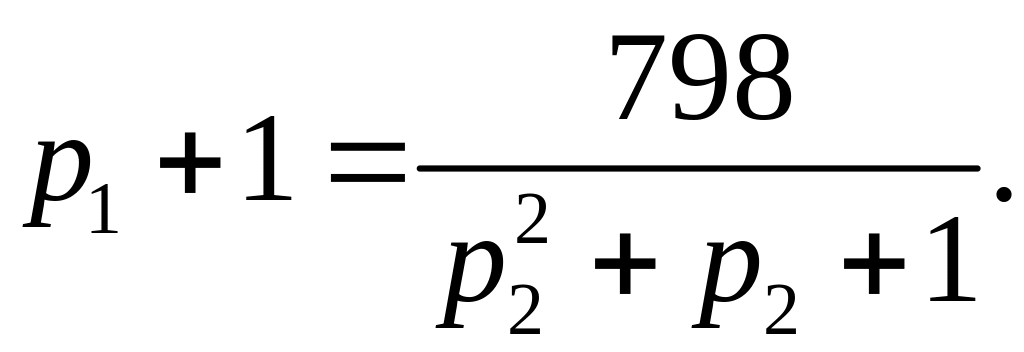 (7)
(7)
Так
как
простое число, то
![]() ,
а
,
а
![]() Так
как
Так
как
![]() и простое число
,
то из (7) следует:
и простое число
,
то из (7) следует:
![]()
4)
Число 113 – простое число и если
![]() ,
то из (7) следует, что
,
то из (7) следует, что
![]() .
.
Рассмотрим
число
![]() где
где
![]() а
,
то есть рассмотрим число
а
,
то есть рассмотрим число
![]() .
.
Число
делителей числа
![]() равно 6 и простые числа
,
равно 6 и простые числа
,
![]() удовлетворяют
условию
удовлетворяют
условию
![]()
![]() .
.
Итак, искомое число .
5)
Число 5 – простое число и если
![]() ,
то из (7) следует, что
,
то из (7) следует, что
![]() .
.
Так
как
простое число, то из последнего уравнения
следует, что
![]() .
.
Рассмотрим число где , а , то есть рас-
смотрим
число
![]() .
Число делителей числа
.
Число делителей числа
![]() ,
равно 6 и простые числа
,
равно 6 и простые числа
![]()
![]() удовлетворяют
условию
удовлетворяют
условию
![]()
![]()
Итак, искомое число .
6) Проверим, существует ли натуральные числа отличные от 452 и 605, которые удовлетворяют условию задачи.
Пусть
![]() .
Так как
.
Так как
![]()
![]()
![]() – нечётное число, то
– нечётное число, то
![]() (случай, когда
(случай, когда
![]() уже рассмотрен). Из равенства
уже рассмотрен). Из равенства
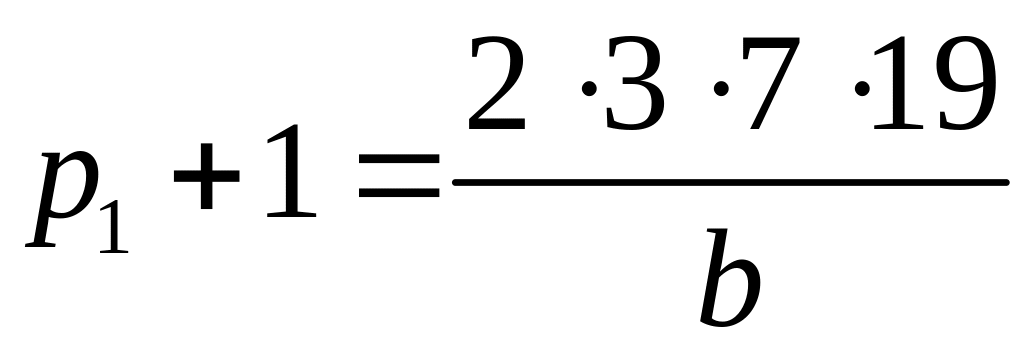 следуют следующие случаи
следуют следующие случаи
-
19
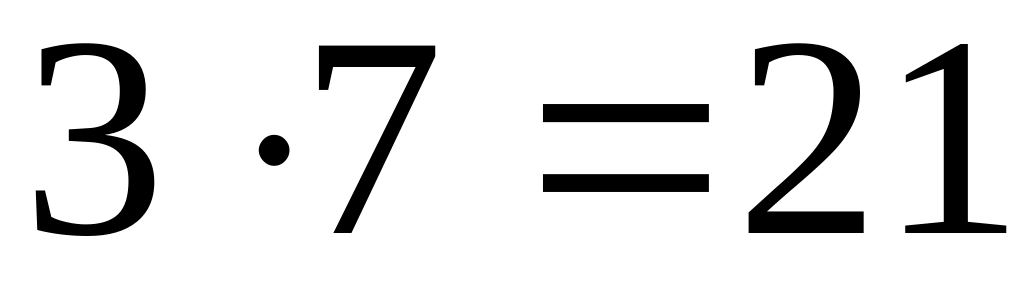
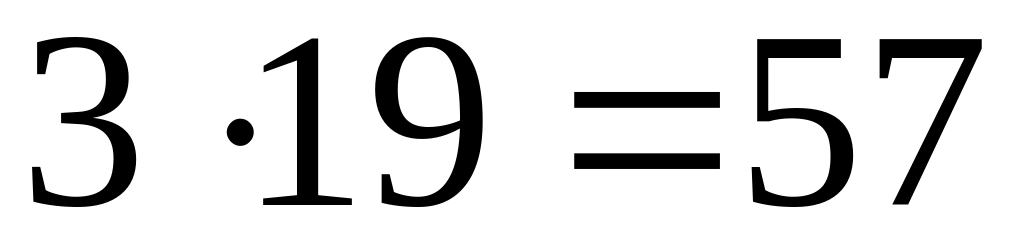
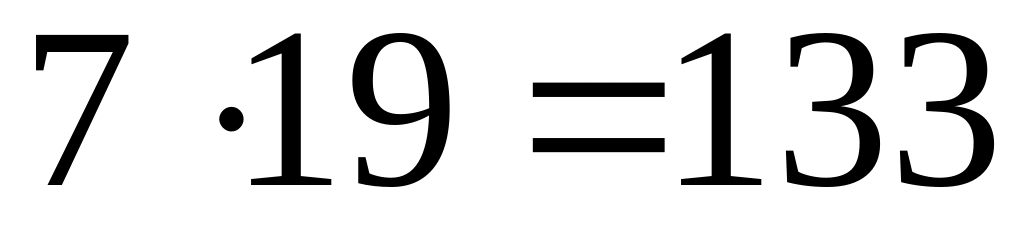
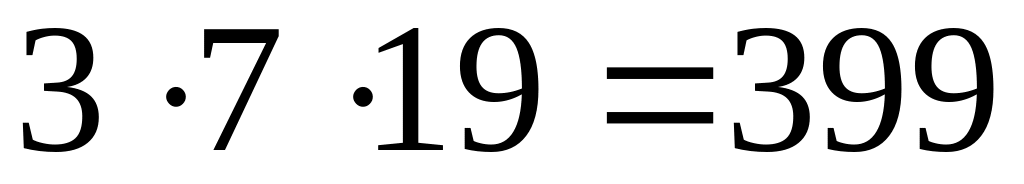
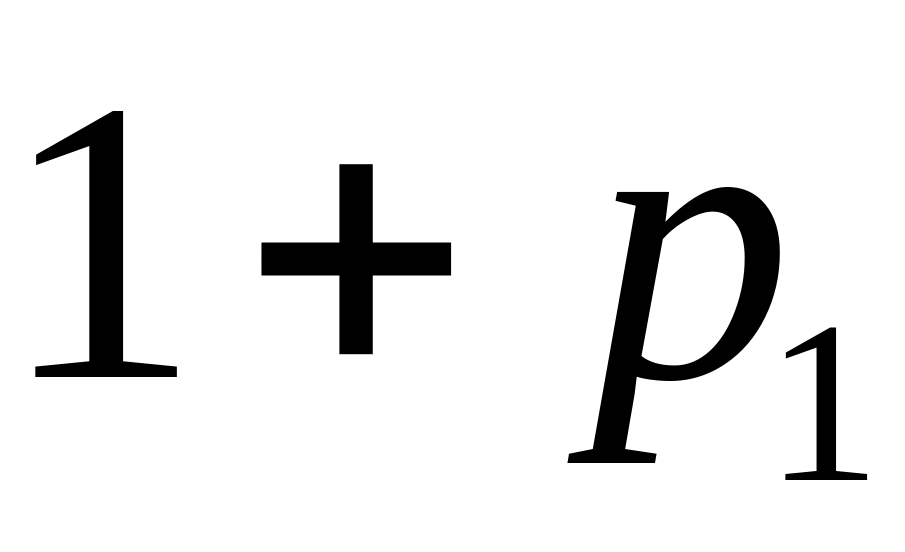
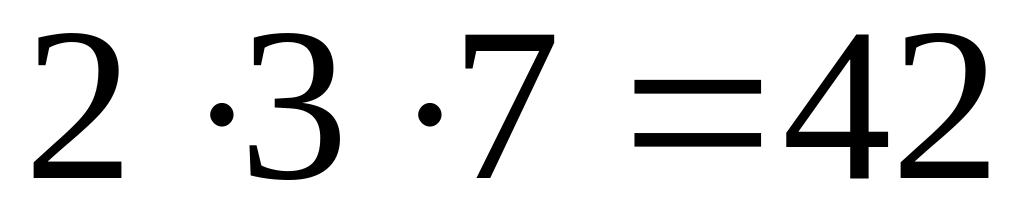

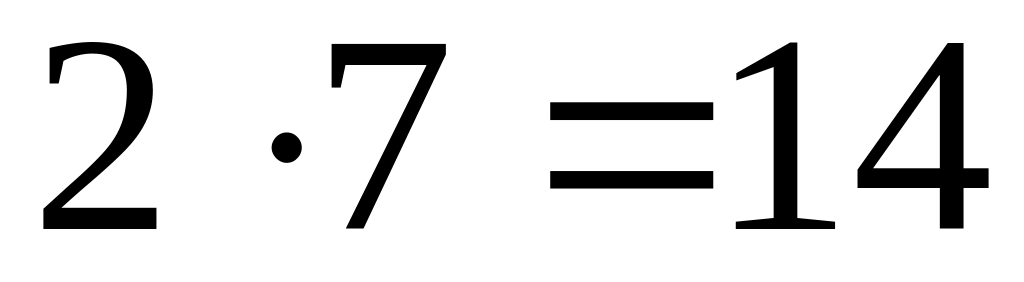

2
41 – простое
37– простое
13– простое
5 случай рассмотрен
1– не простое число
Число может принимать хотя бы одно из значений: 19, 21, 57.
Рассмотрим квадратное уравнение
![]() .
.
Так
как
простое число, то рассматриваемое
уравнение имеет решение, если дискриминант
![]() ,
где
,
где
![]() натуральное число, и
натуральное число, и
![]() простое число.
простое число.
Имеем
![]() .
Рассмотрим уравнение
.
Рассмотрим уравнение
![]()
а)
Если
![]() то
то
![]() Из уравнения
Из уравнения
![]() следует, что
не натуральное число.
следует, что
не натуральное число.
б)
Если
![]() то
то
![]() Находим:
Находим:
![]() а
а
![]() .
Число
не является простым числом.
.
Число
не является простым числом.
в)
Если
![]() ,
то
,
то
![]() Находим:
Находим:
![]() а
а
![]() .
Число
является простым числом, при этом
.
Число
является простым числом, при этом
![]()
Рассмотрим
число
где
![]() а
,
то есть рассмотрим число
а
,
то есть рассмотрим число
![]() .
Число делителей числа
.
Число делителей числа
![]() ,
равно 6 и простые числа
удовлетворяют
условию
,
равно 6 и простые числа
удовлетворяют
условию
![]()
![]()
Итак, искомое число .
Ответ. 452; 605; 637.
2. У натурального числа n ровно 6 натуральных делителей (включая единицу и само число). Сумма этих делителей равна 3906. Найдите все такие числа.
Решение. Пусть искомое натуральное число представлено в виде , где – простые числа, – натуральные числа. Число делителей числа n, включая единицу и число n, равно .
Рассмотрим два случая.
1. Из условия задачи имеем .
1) Так как и – натуральные, не равные единицы числа, то и . Итак, и
2) Найдём .
Делителями числа n являются числа:
Воспользуемся формулой (1)
Из
условия задачи имеем
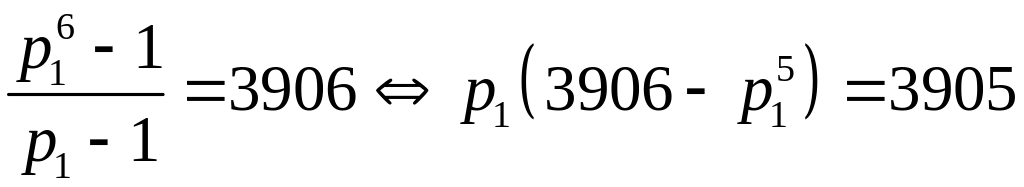 . Рассмотрим
уравнение
. Рассмотрим
уравнение
![]() .
Так как
простое число, 3905 нечётное число, то
.
Так как
простое число, 3905 нечётное число, то
![]() и
и
![]() .
Из последнего неравенства следует, что
.
Из последнего неравенства следует, что
![]() .
Простое число
может
принимать хотя бы одно из значений: 3,
5. Проверкой убеждаемся, что только
удовлетворяют уравнению
.
Простое число
может
принимать хотя бы одно из значений: 3,
5. Проверкой убеждаемся, что только
удовлетворяют уравнению
![]()
Итак,
![]()
Рассмотрим
число
![]() .
Число делителей числа
,
равно 6 и простое число
,
удовлетворяют уравнению
.
Число делителей числа
,
равно 6 и простое число
,
удовлетворяют уравнению
Итак,
искомое число
![]()
2. Из условия задачи имеем, .
1)Так
как
и
– натуральные, не равные единицы числа,
то
![]() и
и
Найдём и . Так как и – натуральные, не равные единицы числа, то (или ) может принимать одно из значений 1 или 2. Пусть и . Тогда
2) Найдём и .
Делителями числа n являются числа:
Воспользуемся формулой (2)
Из условия задачи имеем
![]() (8)
(8)
3) Оценим . Рассмотрим (8).
Так как и простые числа, число 3906 чётное, не кратно 4 и нечётное число, то из (8) следует, что и Тогда .
Из
(8) имеем
 (9)
(9)
Так
как
простое число, то
,
а
.
Так как
и простое число
,
то из (9) следует:
![]()
4)
Число 557 – простое число и если
![]() ,
то из (9) следует,
,
то из (9) следует,
что .
Рассмотрим
число
где
,
а
,
то есть рассмотрим число
![]() .
.
Число
делителей числа
![]() ,
равно 6 и простые числа
,
удовлетворяют
условию
,
равно 6 и простые числа
,
удовлетворяют
условию
![]()
![]() .
.
Итак, искомое число .
5)
Число 5 – простое число и если
,
то из (9) следует, что
![]() .
.
Из последнего уравнения следует, что рассматриваемое квадратное уравнение не имеет корнями простых чисел.
6) Проверим, существует ли натуральные числа отличные от 2228, которые удовлетворяют условию задачи.
Пусть
.
Так как
![]() – нечётное число, то из равенства
– нечётное число, то из равенства
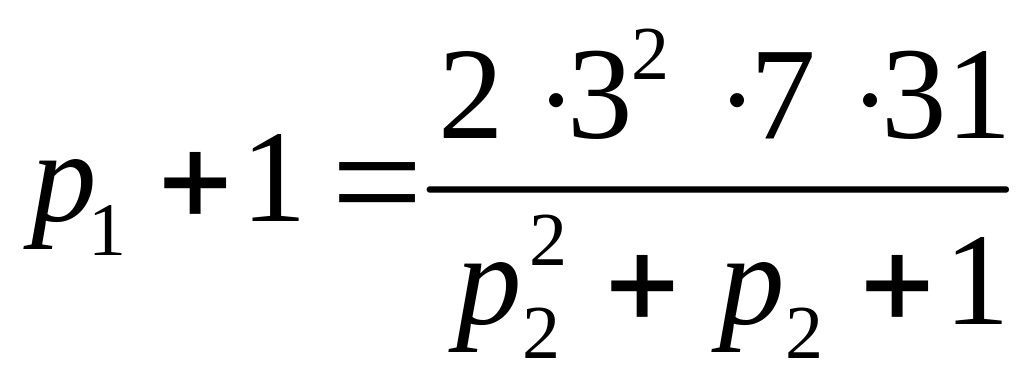 следуют следующие случаи
следуют следующие случаи
-
7
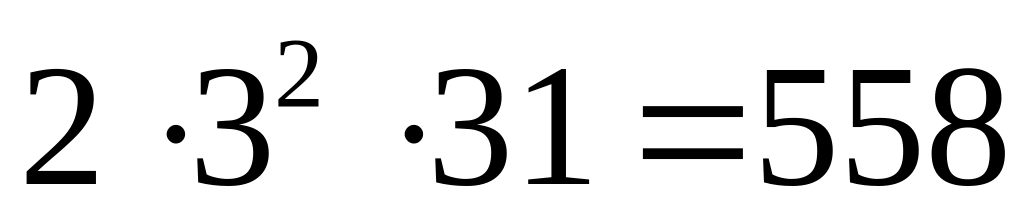
557 – простое
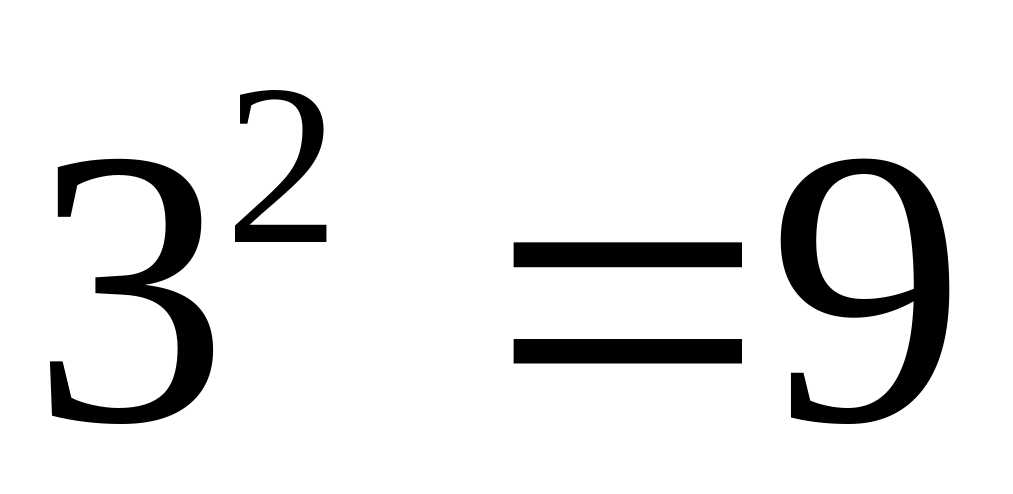
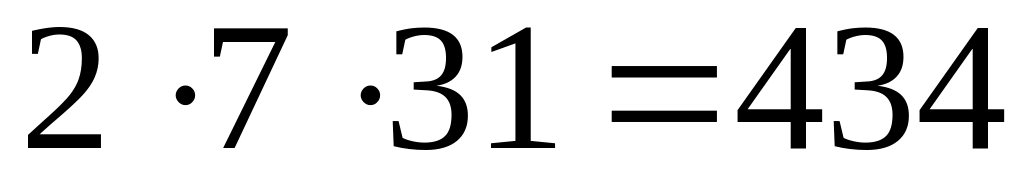
433 – простое
31

125 – не простое
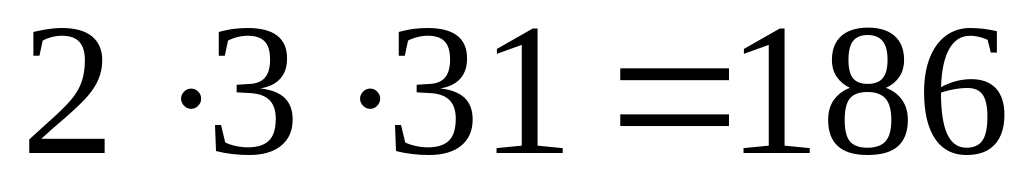
185 – не простое
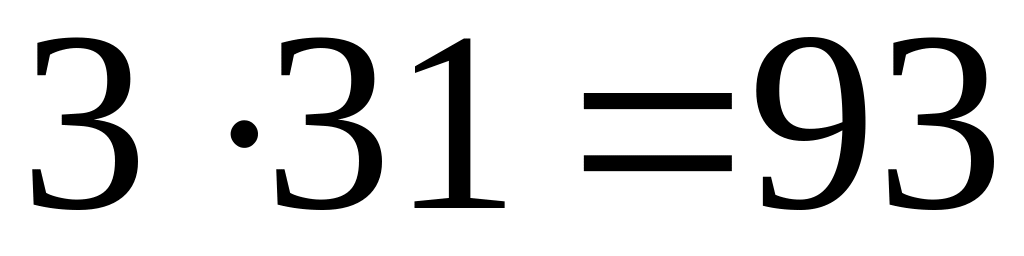
41 – простое
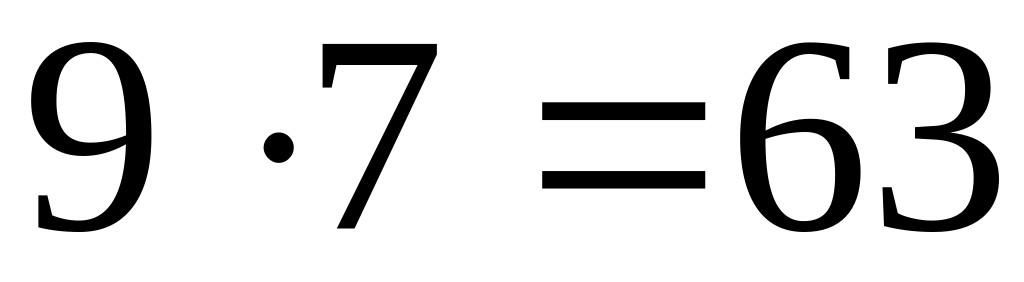

61 – простое

13 – простое

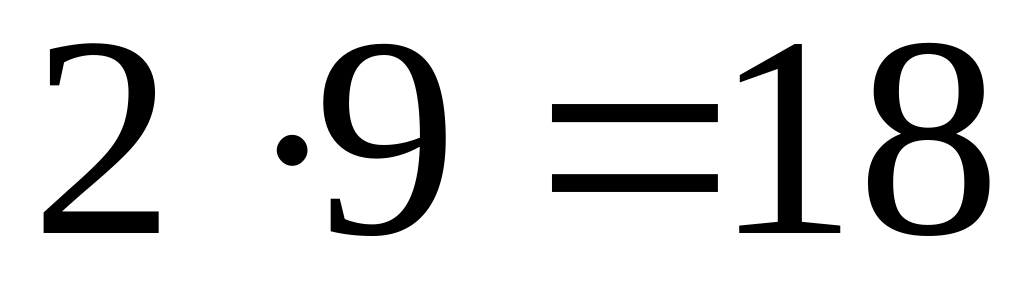
17 – простое

5 – простое
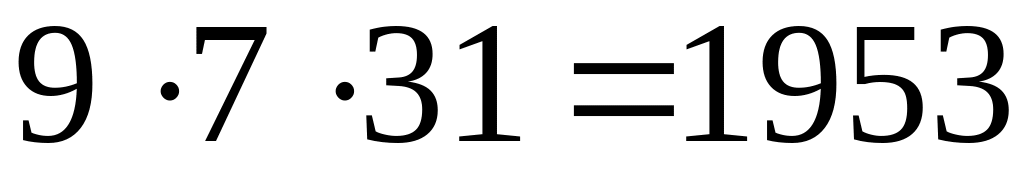

1 – не простое
Отметим:
случаи, когда
,
или
![]() уже
рассмотрены.
уже
рассмотрены.
Итак, может принимать хотя бы одно из значений: 9, 63, 93, 217, 279.
Рассмотрим квадратное уравнение
![]() .
.
Так как простое число, то рассматриваемое квадратное уравнение имеет решение, если дискриминант , где натуральное число, и простое число.
Проверкой убеждаемся, что рассматриваемое квадратное уравнение не имеет корнями простых чисел.
Ответ. 2228; 3125.
3. У натурального числа n ровно 6 натуральных делителей (включая единицу и само число). Сумма этих делителей равна 3500. Найдите это число
Решение. Пусть искомое натуральное число представлено в виде , где – простые числа, – натуральные числа. Число делителей числа n, включая единицу и число n, равно .
Рассмотрим два случая.
1. Из условия задачи имеем .
1) Так как и – натуральные, не равные единицы числа, то и . Итак, и
2) Найдём .
Делителями числа n являются числа:
Воспользуемся формулой (1)
По
условию задачи
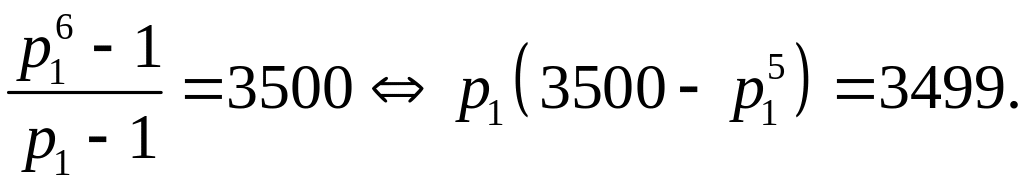
Рассмотрим
уравнение
![]() .
Так как
простое число, и 3499 нечётное число, то
и
.
Так как
простое число, и 3499 нечётное число, то
и
![]() .
Из последнего неравенства следует, что
.
Итак, простое число
может принимать хотя бы одно из значений:
3, 5. Проверкой убеждаемся, что ни
ни
не удовлетворяют уравнению
.
Из последнего неравенства следует, что
.
Итак, простое число
может принимать хотя бы одно из значений:
3, 5. Проверкой убеждаемся, что ни
ни
не удовлетворяют уравнению
![]()
Итак, искомое число не может принимать вид
2. По условию .
1)Так как и – натуральные, не равные единицы числа, то и
Найдём и . Так как и –
натуральные, не равные единицы числа, то (или ) может принимать одно из значений 1 или 2. Пусть и . Тогда
2) Найдём и .
Делителями числа n являются числа: Воспользуемся формулой (2)
Из
условия задачи имеем
![]() (10)
(10)
3) Оценим . Рассмотрим (10).
Так
как
и
простые числа, число 3500 чётное, кратное
4,
нечётное число, то из (10) следует, что
![]()
Из
(10) имеем
 (11)
(11)
Так
как
простое число, то
,
а
.
Так как
и простое число
![]() то из (11) следует:
то из (11) следует:
![]()
4) Так как числа 3 и 499 – простые числа, то рассмотрим следующие случаи.
а)
Если
![]() ,
то из (11) следует, что
,
то из (11) следует, что
![]()
Рассматриваемое квадратное уравнение не имеет корнями простых чисел.
б)
Если
![]() ,
то из (11) следует, что
– простое число.
,
то из (11) следует, что
– простое число.
Рассмотрим
число
где
,
а
,
то есть рассмотрим число
![]() .
.
Число
делителей числа
![]() ,
равно 6 и числа
,
удовлетворяют
условию
,
равно 6 и числа
,
удовлетворяют
условию
![]()
![]() .
.
Итак, искомое число .
5) Проверим, существует ли натуральные числа, отличные от 1996, которые удовлетворяют условию задачи.
Отметим,
что
![]() .
Пусть
.
Так как
– нечётное число,
.
Пусть
.
Так как
– нечётное число,
![]() – чётное число, то из равенства
– чётное число, то из равенства
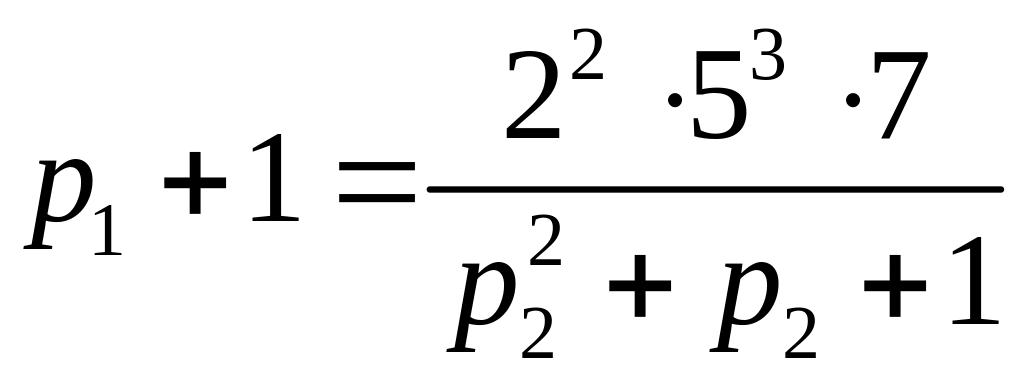 следуют следующие случаи (отметим:
случаи, когда
,
следуют следующие случаи (отметим:
случаи, когда
,
![]() уже
рассмотрены).
уже
рассмотрены).
-

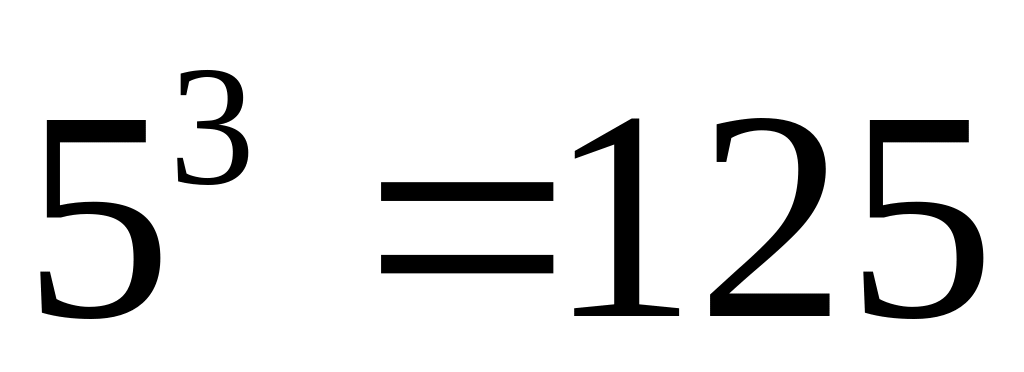

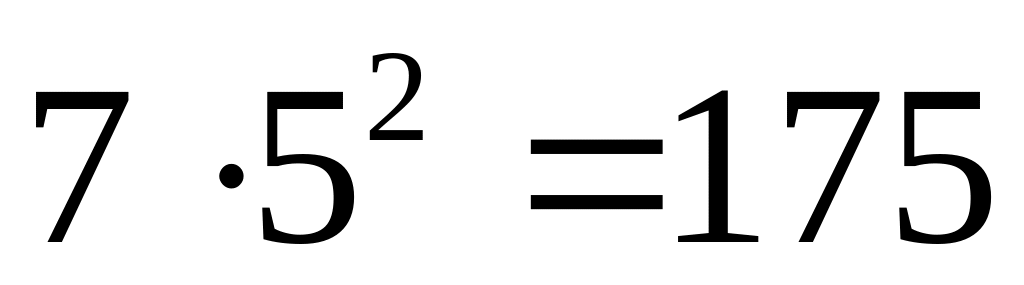


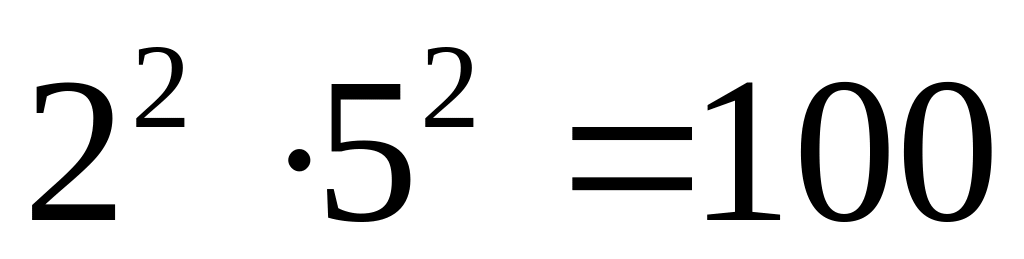
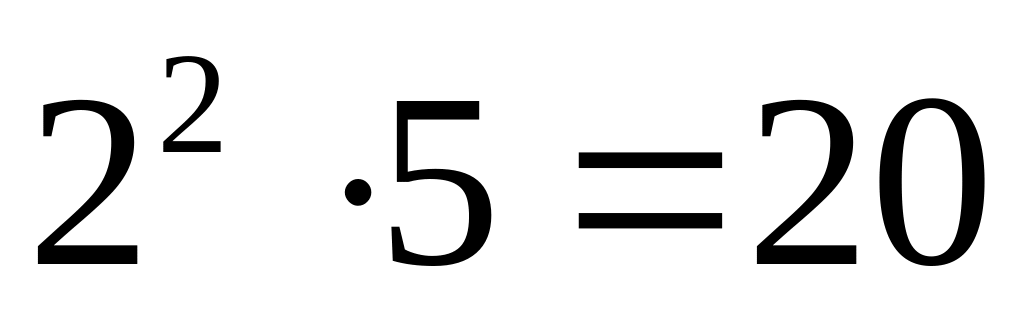
139 – простое
27 – не простое
99 – не простое
19 – простое
Итак, может принимать хотя бы одно из значений: 25, 175.
Корнем квадратного уравнения , где принимает одно из значений 25 или 175, не является простое число.
Ответ. 1906.
4. У натурального числа n ровно 7 натуральных делителей (включая единицу и само число). Сумма этих делителей равна 19 531. Найдите это число.
Решение. Пусть искомое натуральное число представлено в виде , где – простые числа, – натуральные числа. Число делителей числа n, включая единицу и число n, равно .
1.
Из условия задачи имеем
![]() .
.
1)
Так как
и
– натуральные, не равные единицы числа,
то
и
.
Итак,
![]() и
и
![]()
2) Найдём .
Делителями
числа n
являются
числа:
![]() Воспользуемся формулой (1)
Воспользуемся формулой (1)
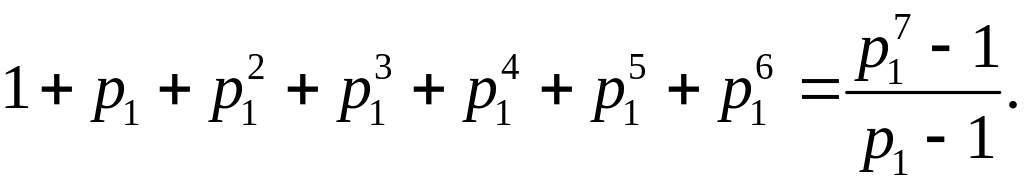
По
условию задачи

![]()
Рассмотрим уравнение
Так
как
простое число, и
![]() ,
то
,
то
![]() .
Итак,
может принимать хотя бы одно из следующих
значений: 2, 3, 5.
.
Итак,
может принимать хотя бы одно из следующих
значений: 2, 3, 5.
Проверкой
убеждаемся, что только
![]() удовлетворяет
уравнению
удовлетворяет
уравнению
Рассмотрим
число
![]() где
,
то есть рассмотрим число
где
,
то есть рассмотрим число
![]() .
.
Число
делителей числа
![]() равно 6 и простое число
,
удовлетворяют уравнению
равно 6 и простое число
,
удовлетворяют уравнению
Итак, искомое число .
Ответ.
![]()
5. У натурального числа n ровно 8 натуральных делителей (включая единицу и само число). Сумма этих делителей равна 1620. Найдите все такие числа.
Решение. Пусть искомое натуральное число представлено в виде
, где – простые числа, – натуральные числа. Число делителей числа n, включая единицу и число n, равно .
Рассмотрим три случая.
1.
По условию
![]() .
.
1)
Так как
и
– натуральные, не равные единицы числа,
то
и
.
Итак,
![]() и
и
![]()
2) Найдём .
Делителями
числа n
являются
числа:
![]()
Воспользуемся формулой (1)
![]()
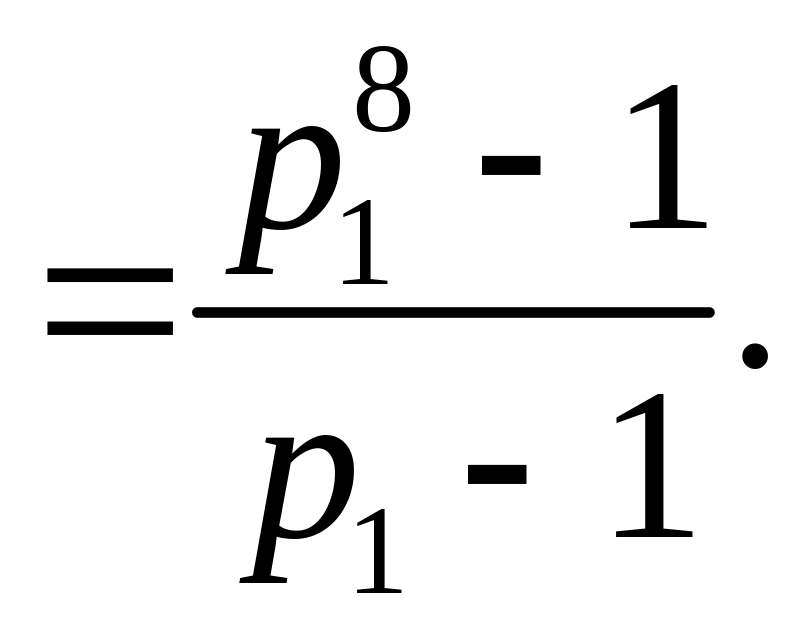
По
условию задачи

Рассмотрим
уравнение
![]() .
Так как
простое число, 1619 нечётное число, то
и
.
Так как
простое число, 1619 нечётное число, то
и
![]() .
Из последнего неравенства следует, что
.
Из последнего неравенства следует, что
![]() .
Проверкой убеждаемся, что
не удовлетворяет уравнению
.
Проверкой убеждаемся, что
не удовлетворяет уравнению
![]()
Искомое число не может принимать вид
2.
По условию
![]() .
.
1)Так
как
![]() и
– натуральные, не равные единицы числа,
то
и
и
– натуральные, не равные единицы числа,
то
и
Найдём
и
.
Так как
![]() и
– натуральные, не равные единицы числа,
то
(или
)
может принимать одно из значений 1 или
3. Пусть
и
и
– натуральные, не равные единицы числа,
то
(или
)
может принимать одно из значений 1 или
3. Пусть
и
![]() .
Тогда
.
Тогда
![]()
2) Найдём и .
Делителями числа n являются числа:
![]()
Воспользуемся формулой (3)
![]() Из
условия задачи имеем
Из
условия задачи имеем
![]()
3)
Отметим, что
![]()
Рассмотрим уравнение
![]() (12)
(12)
Очевидно,
числа
![]() одинаковой чётности.
одинаковой чётности.
Пусть числа чётные.
Так
как числа
чётные, то из уравнения (12) следует, что
число
нечётное, что возможно только в случае,
когда
![]() .
Если
,
то из уравнения (12) следует, что
.
Если
,
то из уравнения (12) следует, что
![]()
Так
как числа
чётные и
![]() то возможны следующие случаи:
то возможны следующие случаи:
а)
![]()
![]()
б)
![]() не простое число.
не простое число.
в)
![]()
![]()
Из
а) и б) следует, если
,
то не существует простого числа
![]() которое удовлетворяет уравнению (12).
которое удовлетворяет уравнению (12).
Пусть числа нечётные.
Число
![]() нечётное, если
нечётное, если
![]()
Если
,
то
![]() и
и
![]() .
Из уравнения (12) следует, что
.
Из уравнения (12) следует, что
![]()
Число 107 – простое число.
4)
Рассмотрим число
![]() где
где
![]() ,
а
,
то есть рассмотрим число
,
а
,
то есть рассмотрим число
![]() .
.
Число
делителей числа
![]() ,
равно 8 и простые числа
,
удовлетворяют
условию
,
равно 8 и простые числа
,
удовлетворяют
условию
![]()
Искомое число .
3.
По условию
![]() .
.
Так
как
![]() и
– натуральные не равные единицы числа,
то
и
– натуральные не равные единицы числа,
то
![]() и
и
![]()
1)
Найдём
и
![]() .
Так как
,
.
Так как
,![]() –
натуральные, не равные единицы числа,
то из равенства
–
натуральные, не равные единицы числа,
то из равенства
![]() следует, что
следует, что
![]() Таким образом,
Таким образом,
![]()
2)
Найдём
,
и
![]()
Делителями числа n являются числа:
![]()
Воспользуемся формулой (4)
По
условию задачи имеем
![]()
3) Рассмотрим уравнение
![]() (13)
(13)
Так
как
![]() целые числа и правая часть уравнения
(13) равна
целые числа и правая часть уравнения
(13) равна
![]() ,
то один или два сомножителя левой части
уравнения (13) чётные.
,
то один или два сомножителя левой части
уравнения (13) чётные.
Отметим,
что число
![]() ,
где
,
где
![]() простое число, нечётное только в случае,
когда
простое число, нечётное только в случае,
когда
![]() .
Так как числа
.
Так как числа
![]() простые и разные, то только один
сомножитель левой части уравнения (13)
нечётный.
простые и разные, то только один
сомножитель левой части уравнения (13)
нечётный.
Пусть
число
нечётное, тогда
.
Если
,
то из уравнения (13) следует:
![]() .
Так как числа
разные и
,
то
.
Так как числа
разные и
,
то
![]() .
Тогда
.
Тогда
![]() чётные числа. Поэтому
возможны
следующие случаи
чётные числа. Поэтому
возможны
следующие случаи
|
|
|
|
|
5 простое |
|
89 простое |
|
17 простое |
|
29 простое |
|
53 простое |
|
9 не простое |
Если
,
то из таблице следует, что уравнение
(13) имеет два решения – это
![]()
![]() или
или
![]()
![]() .
.
Рассмотрим
число
![]() где
где
![]() ,
то есть рассмотрим число
,
то есть рассмотрим число
![]() .
.
Число
делителей числа
![]() ,
равно 8 и простые числа
,
удовлетворяют
условию
,
равно 8 и простые числа
,
удовлетворяют
условию
![]() .
.
Искомое число .
Рассмотрим
число
![]() где
где
![]() ,
то есть рассмотрим число
,
то есть рассмотрим число
![]() .
.
Число
делителей числа
![]() ,
равно 8 и простые числа
,
удовлетворяют
условию
,
равно 8 и простые числа
,
удовлетворяют
условию
![]() .
.
Искомое число .
Ответ. 856; 890; 986.
6. У натурального числа n ровно 9 натуральных делителей (включая единицу и само число). Сумма этих делителей равна 9517. Найдите такое число.
Решение. Пусть искомое натуральное число представлено в виде , где – простые числа, – натуральные числа. Число делителей числа n, включая единицу и число n, равно .
Рассмотрим два случая.
1.
По условию
![]() .
.
1)
Так как
и
– натуральные, не равные единицы числа,
то
и
.
Итак,
![]() и
и
![]()
2) Найдём .
Делителями
числа n
являются
числа:
![]() Воспользуемся формулой (1)
Воспользуемся формулой (1)
![]()
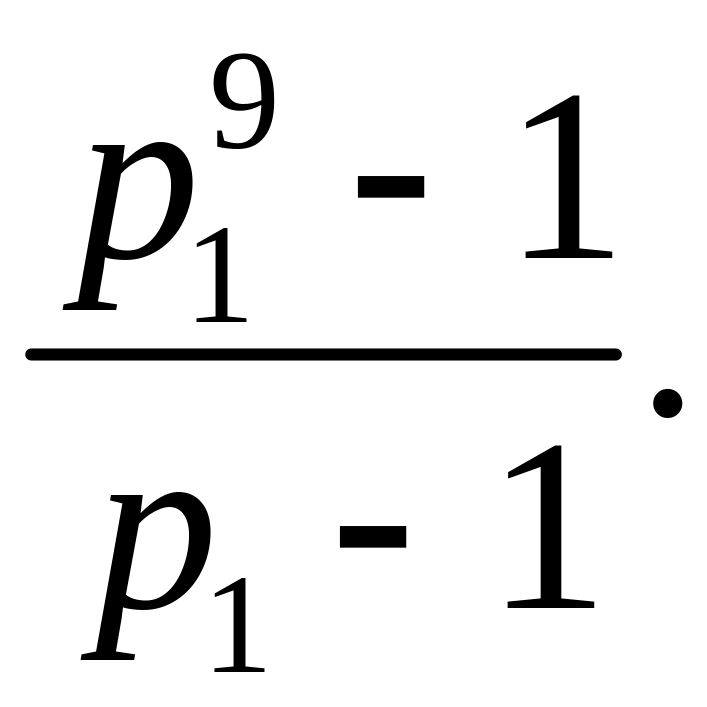
По
условию задачи
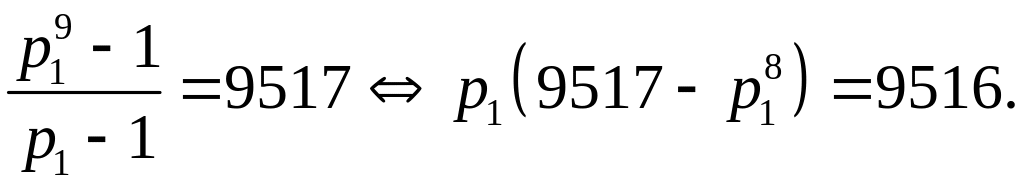
Рассмотрим
уравнение
![]() .
Из неравенства
.
Из неравенства
![]() следует,
что
.
Проверкой убеждаемся, что ни
ни
не удовлетворяют уравнению
.
следует,
что
.
Проверкой убеждаемся, что ни
ни
не удовлетворяют уравнению
.
Искомое число не может принимать вид
2.
По условию
![]() .
.
1)Так
как
![]() и
– натуральные, не равные единицы числа,
то
и
и
– натуральные, не равные единицы числа,
то
и
Найдём
и
.
Так как
![]() и
– натуральные, не равные единицы числа,
то
и
– натуральные, не равные единицы числа,
то
![]() ,
,
![]()
![]() .
.
2) Найдём и .
Делителями числа n являются числа:
![]()
Воспользуемся формулой (5)

По условию задачи
![]() Так
как последнее уравнение симметрично
относительно
Так
как последнее уравнение симметрично
относительно
![]() а числа 307, 31 – простые, то
а числа 307, 31 – простые, то
![]() находим из системы
находим из системы
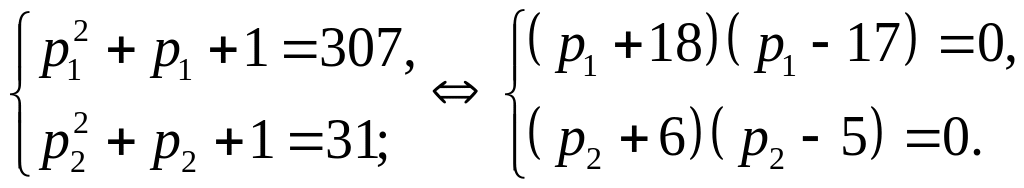
Так
как
простые числа, то последней системе,
удовлетворяют числа
![]()
Рассмотрим
число
![]() где
где
![]() то
есть рассмотрим число
то
есть рассмотрим число
![]()
Число
делителей числа
![]() ,
равно 9 и простые числа
,
равно 9 и простые числа
![]() удовлетворяют
условию
удовлетворяют
условию
![]()
Искомое число .
Ответ. 7225.
7. Докажите, что натуральное число имеет нечётное число делителей (включая единицу и само число) тогда и только тогда, когда оно является квадратом натурального числа.
Доказательство.
Пусть натуральное число а,
имеет нечётное число делителей, включая
единицу и число а.
Пусть
![]() ,
где
– простые числа,
–
натуральные числа. Число делителей
числа а,
включая единицу и число а,
равно
.
,
где
– простые числа,
–
натуральные числа. Число делителей
числа а,
включая единицу и число а,
равно
.
Так
как
нечётное число, то все числа
![]() являются нечётными, а тогда все числа
являются нечётными, а тогда все числа
![]() являются чётными.
являются чётными.
Пусть
![]() .
Тогда
.
Тогда
![]()
Доказали, что число а является квадратом натурального числа.
Пусть натуральное число а является квадратом натурального
числа
,
то
есть
![]()
Пусть
![]() ,
где
,
где
![]() – простые числа,
– простые числа,
![]()
![]() –
натуральные числа. Тогда
–
натуральные числа. Тогда
![]()
![]()
Число
делителей числа а,
включая единицу и число а,
равно
![]() .
Так как
.
Так как
![]() – нечётные
числа, то число
– нечётные
числа, то число
![]() являются нечётным числом.
являются нечётным числом.
Доказали, что квадрат натурального числа имеет нечётное число делителей (включая единицу и само число).
