6.2 Різниці решітчастих функцій

Першою похідною безперервної функції f(x) називається відношення приросту функції до приросту аргументу, якщо він прямує до нуля:

.

Якщо виконати дискретизацію безперервної функції, замінивши безперервний аргумент t на дискретний nT, де n = 0, 1, 2…N, T – період дискретизації, отримаємо дискретний аналог першої похідної – першу пряму різницю решітчастої функції:

.

Аналогічно замінюються похідні другого і вищих порядків:

.

Пряма різниця записується моменту часу , якщо відомі значення функції і . У випадку, коли відомі поточне і попереднє значення функції, записується зворотна різниця:

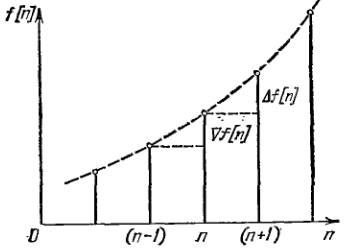
Зворотні різниці другого і вищих порядків записуються за формулами:

,

.

6.3 Різницеві рівняння

Різницеві рівняння за своїми властивостями та областями застосування досить близькі до диференціальних рівнянь. Відмінність полягає у тому, що диференціальні рівняння зв’язують значення функції та її похідних в один і той же момент часу:

,

а різницеві рівняння  значення функції у різні моменти часу:

.

Однорідне лінійне різницеве рівняння з постійними коефіцієнтами має вигляд:

(1)

Отримати різницеві рівняння можна декількома способами:

• дискретизацією звичайних диференціальних рівнянь;

• складанням математичних моделей об’єктів з дискретним часом;

• аналізом математичних рядів та рекурентних співвідношень.

21. Різницеві рівняння.

Різницеві рівняння за своїми властивостями та областями застосування досить близькі до диференціальних рівнянь. Відмінність полягає у тому, що диференціальні рівняння зв’язують значення функції та її похідних в один і той же момент часу:

,

а різницеві рівняння  значення функції у різні моменти часу:

.

Однорідне лінійне різницеве рівняння з постійними коефіцієнтами має вигляд:

(1)

Отримати різницеві рівняння можна декількома способами:

• дискретизацією звичайних диференціальних рівнянь;

• складанням математичних моделей об’єктів з дискретним часом;

• аналізом математичних рядів та рекурентних співвідношень.

Дискретизація диференціальних рівнянь

Приклад 1. Виконати дискретизацію диференціального рівняння.

.

Замінимо першу та другу похідні відповідними різницями (2.4) і (2.5).

,

Зведемо подібні та отримаємо шукане різницеве рівняння:

.

Різницеві рівняння можна розглядати як рекурентні співвідношення, що дозволяють обчислювати значення при k = 0, 1, 2… для заданих початкових значень і рівняння виду (1)

22. Z – перетворення. Загальні відомості.

Z-перетворенням (перетворенням Лорана) називають згортання вихідного сигналу, заданого послідовністю дійсних чисел у часовій області, в аналітичну функцію комплексної частоти. Якщо сигнал являє імпульсну характеристику лінійної системи, то коефіцієнти Z-перетворення показують відгук системи на комплексні експоненти  , тобто на гармонійні осциляції з різними частотами і швидкостями наростання / загасання.

Z-перетворення, як і багато інтегральних перетворень, може бути як одностороннє, так і двостороннє.