4.1.1. Побудова схеми та укрупненої схеми мережі полігонометричних ходів за вихідними пунктами
Схему мережі полігонометричних ходів будуємо так:
Складаємо саму схему, де підписуємо назви (номери) всіх пунктів (точок), а також номери ходів. У вузлах відображаємо напрями. Виписуємо виміряні кути (позначаються дугами) та довжини ліній (горизонтальні прокладення).
На укрупненій схемі мережі вказуємо назви вихідних та вузлових пунктів та напрямів. В стовпчик записуємо такі дані: номер ходу, суму виміряних приростів, нев’язки, довжину ходу, кількість ходів.
У способі послідовних наближень використовуємо лише укрупнену схему полігонометричних ходів 4 класу.
4.1.2. Зрівноваження мережі та оцінка точності отриманих результатів
Роздільне зрівноваження мережі полігонометричних ходів можна проводити: способом еквівалентної заміни, способам послідовних наближень (вузлів), способом полігонів В.В. Попова. Цими способами спочатку отримують дирекційні кути вузлових напрямків і координати вузлових пунктів, а потім, використовуючи їх як вихідні, зрівноважують окремі ходи також нестрогим способом, розподіляючи нев’язки в прирости координат прямо пропорційно до числа лінії або до довжин ліній.
В курсовій роботі мережу полігонометричних ходів будемо зрівноважувати способом послідовних наближень. Спочатку складаємо укрупнену схему мережі полігонометричних ходів 4 класу (рис. 5.1).
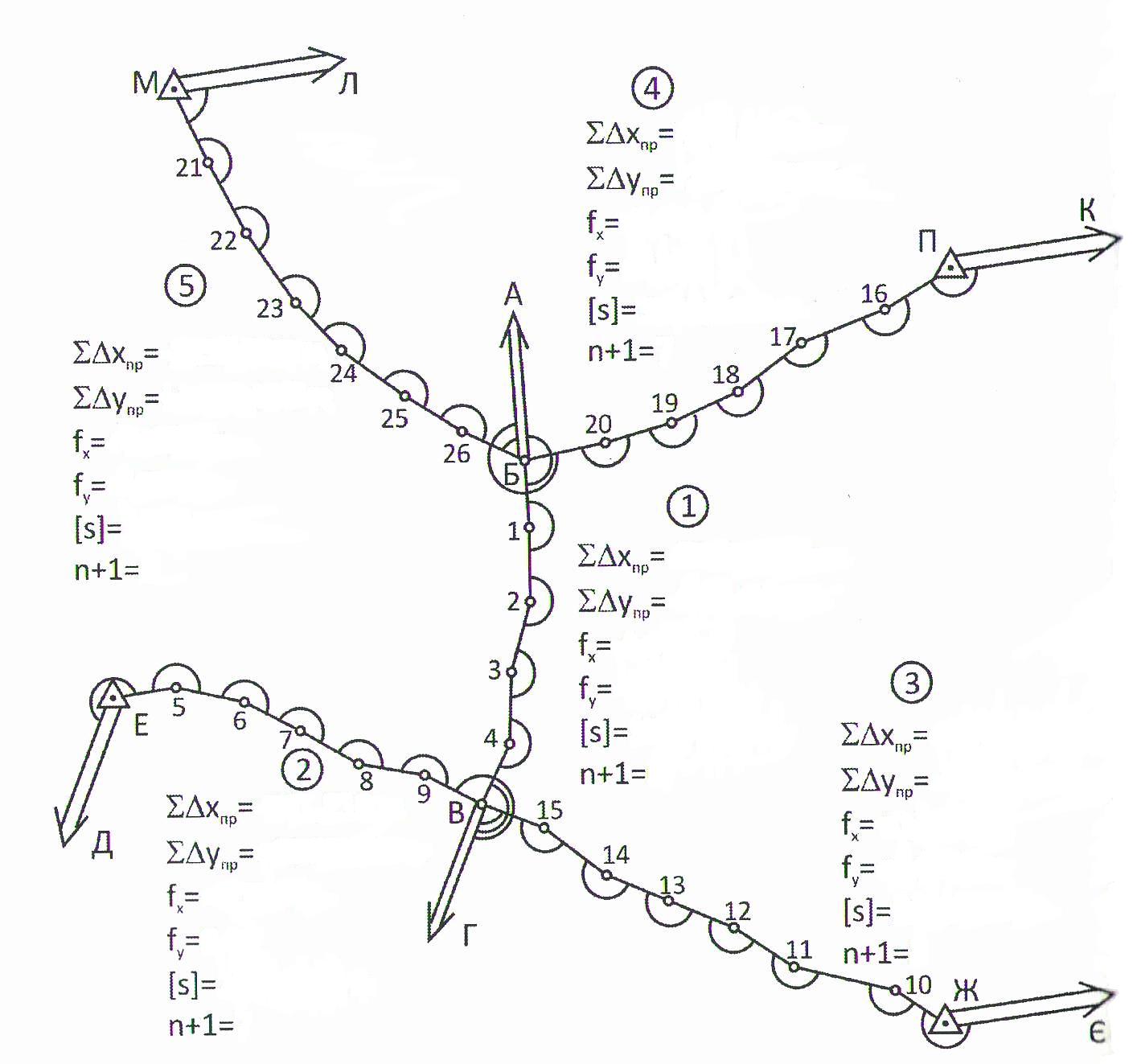
Рис. 4.1 Укрупнена схема мережі полігономертичних ходів 4 класу
Обчислення починаємо із розрахунку дирекційних кутів вихідних напрямків. За координатами вихідних пунктів знаходимо румби:
r
= arctg
Дирекційні кути напрямку КП вираховуємо за румбом з врахуванням чверті, в якій він знаходиться, а чверть визначаємо за знаками приростів координат (ΔХ; ΔY). Формули для вирахування дирекційних кутів за румбами наведені в ( таб. 5.1).
Таблиця 4.1
Знаходження дирекційного кута за румбами
-
№ чверті
Знаки приростів
Формули
І
α = r
ІІ
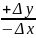
α = 180˚- | r |
ІІІ
α = 180˚+ r
ІV
α = 360˚- | r |
Далі вираховуємо суми кутів в кожному ході. Далі способом послідовних наближень зрівноважуємо дирекційні кути вузлових напрямків Б-А та В-Г (таб. 5.2) в наступній послідовності. Спочатку заповнюємо графи 1-6 таблиці 5.2. Далі вираховуємо вагу кожного ходу за формулою:
pα=
і записуємо в графу 7. Значення дирекційного кута вузлового напрямку
Б-А отримуємо двічі з ходів 4 та 5, використовуючи формулу:
αк= αп+Σβл -180˚(n+1)
Ця формула справедлива для лівих виміряних кутів. Перше наближення дирекційного кута Б-А отримуємо як середнє вагове із значень, вирахуваних з ходів 4 та 5.
Перше наближення дирекційного кута В-Г отримуємо як середнє вагове із значень, вирахованих з ходів 1, 2, 3. Для вирахування дирекційного кута В-Г з ходу 1 використовується не кут Б-А, отриманий в першому наближенні, а зворотний йому А-Б.
Після виконання першого наближення переходимо до другого, дирекційні кути вузлових напрямків обчислюємо в тій самій послідовності. Друге наближення дирекційного кута Б-А отримуємо вже як середнє вагове із значень, вирахуваних із ходів 1, 4, 5. При вирахуванні в другому та наступних наближеннях дирекційного кута Б-А з ходу 1, напрямок ходу змінюється на протилежний, отже виміряні кути β будуть правими і дирекційний кут беде вираховуватись за формулою:
αк= αп-Σβп +180˚(n+1)
Крім цього, вирахуваний в попередньому наближенні дирекційний кут В-Г змінюємо на зворотній Г-В. обчислення закінчено, коли значення в останніх наближень не будуть відрізнятись між собою (в цілих секундах).
Далі визначаємо поправки υβі на кожен хід як різницю між кінцевим значенням і отриманим з і-го ходу в останньому наближенні.
υβі =α - α'
Отримавши зрівноважені значення дирекційних кутів вузлових напрямків переходимо до зрівноваження координат вузлових точок. Для цього знаходимо практичні суми приростів ходів, які вираховуємо у відомості вирахування полігонометричних ходів (таб. 5.5). Зрівноваження координат вузлових точок теж виконуємо способом послідовних наближень окремо для абсцис та ординат. Зрівноваження виконуємо у такому порядку:
Заповнюємо графи 1-6 таблиць 4.3, 4.4. Далі вираховуємо ваги суми приростів для кожного ходу за формлою:
px
= py
=
Значення абсциси та ординати вузлової точки Б в першому наближенні вираховуємо з ходів 4 і 5 за формулами:
Xк= Xп +ΣΔx
Yк= Yп +ΣΔy
Значення координат вузлової точки В в першому наближенні вираховуємо з ходів 1, 2 та 3, використовуючи для першого ходу абсциси та ординати точки Б, отримані в першому наближенні.
Далі переходимо до другого наближення, вираховуючи абсциси і ординати вузлових точок в тій самій послідовності. За вихідні при кожному наступному вирахуванні приймають значення координат, отриманих з попередніх наближень. Закінчують вирахування тоді, коли значення двох останніх наближень не будуть відрізнятись між собою (в міліметрах).
Далі вираховуємо поправки υх та υу на кожен хід як різницю між кінцевим значенням і отриманих по ходу в останньому наближенні.
υх = X - X'i
υу = Y - Y'i
Отримавши зрівноважені значення координат вузлових точок записуємо їх у відомості вирахування координат точок полігонометричних ходів (таб. 4.5). Далі знаходимо теоритичну суму приростів, вираховуємо нев’язки то вводимо поправки у виміряні прирости. Отримуємо виправлені прирости і розраховуємо координати усіх точок полігонометричних ходів. Всі розрахунки наведені в таблиці 4.5.
Далі виконуємо оцінку точності польових вимірів та зрівноважених значень дирекційних кутів вузлових напрямків та оцінку точності координат вузлових точок.
У відомостях обчислення координат я обчислив дирекційні кути напрямків та за приростами координат розрахував координати точок ходу.
Обчислення дирекційних кутів вузлових напрямків БА та ВГ я виконала способом послідовних наближень. Аналогічно я обчислював значення абсцис та ординат вузлових точок .
Відомість вирахування координат точок полігонометричних ходів 4 класу |
||||||||||||||||
№ |
Виміряні кути β |
Виправлені кути β |
Дирекційні кути α |
Довжини ліній S, м |
Прирости координат, м |
Координати, м |
||||||||||
Виміряні |
Виправлені |
|||||||||||||||
∆Χ |
∆Υ |
∆Χ |
∆Υ |
Χ |
Υ |
|||||||||||
Хід 1 |
||||||||||||||||
А |
° |
′ |
″ |
° |
′ |
″ |
° |
′ |
″ |
|
|
|
|
|
|
|
|
|
|
1,3 |
|
|
|
191 |
57 |
08 |
|
|
|
|
|
|
|
Б |
158 |
44 |
43,0 |
158 |
44 |
44,3 |
|
|
|
|
2 |
3 |
|
|
13137,961 |
14849,776 |
|
|
|
1,3 |
|
|
|
170 |
41 |
52,3 |
482,462 |
89,801 |
458,400 |
89,802 |
458,402 |
|
|
1 |
195 |
04 |
4,0 |
195 |
04 |
5,3 |
|
|
|
|
2 |
3 |
|
|
13227,763 |
15308,178 |
|
|
|
1,3 |
|
|
|
185 |
45 |
57,6 |
469,957 |
78,849 |
471,274 |
78,850 |
471,277 |
|
|
2 |
173 |
34 |
53,0 |
173 |
34 |
54,3 |
|
|
|
|
2 |
3 |
|
|
13306,613 |
15779,455 |
|
|
|
1,4 |
|
|
|
179 |
20 |
51,9 |
477,619 |
-55,366 |
459,382 |
-55,364 |
459,384 |
|
|
3 |
195 |
14 |
40 |
195 |
14 |
41,4 |
|
|
|
|
2 |
2 |
|
|
13251,249 |
16238,839 |
|
|
|
1,4 |
|
|
|
194 |
35 |
33,3 |
420,758 |
40,307 |
412,920 |
40,309 |
412,923 |
|
|
4 |
197 |
54 |
19,0 |
197 |
54 |
20,4 |
|
|
|
|
2 |
2 |
|
|
13291,558 |
16651,762 |
|
|
|
1,3 |
|
|
|
212 |
29 |
50,7 |
418,618 |
-66,584 |
391,526 |
-66,583 |
391,528 |
|
|
В |
177 |
27 |
9,0 |
177 |
27 |
10,3 |
|
|
|
|
|
|
|
|
13224,975 |
17043,290 |
|
|
|
|
|
|
|
210 |
00 |
04 |
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1098 |
02 |
48 |
|
P = [S] = |
2269,414 |
м |
|
87,006 |
м |
|
|
2193,502 |
м |
||
|
1098 |
2 |
58,11 |
|
|
|
|
|
|
|
87,015 |
м |
|
|
2193,514 |
м |
|
0 |
0 |
7,89 |
|
|
|
|
|
|
|
-0,008 |
м |
|
|
-0,012 |
м |
|
0 |
0 |
12,25 |
|
|
|
|
|
|
|
0,015 |
м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1/150400 |
|
|||
+
±
|
Відомість вирахування координат точок полігонометричних ходів 4 класу |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
№ |
Виміряні кути β |
Виправлені кути β |
Дирекційні кути α |
Довжини ліній S, м |
Прирости координат, м |
Координати, м |
|
||||||||||||||||||||||||||||||||||||||||
|
Виміряні |
Виправлені |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
∆Χ |
∆Υ |
∆Χ |
∆Υ |
Χ |
Υ |
|
|||||||||||||||||||||||||||||||||||||||||
|
Хід 2 |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Д |
° |
′ |
″ |
° |
′ |
″ |
° |
′ |
″ |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
238 |
13 |
50 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
Е |
207 |
57 |
16,0 |
207 |
57 |
18,3 |
|
|
|
|
-2 |
6 |
|
|
10762,730 |
16775,599 |
|
||||||||||||||||||||||||||||||
|
|
|
|
3 |
|
|
|
266 |
11 |
8,3 |
413,056 |
394,836 |
-132,403 |
394,834 |
-132,397 |
|
|
|
||||||||||||||||||||||||||||||
|
5 |
196 |
16 |
0,0 |
196 |
16 |
2,3 |
|
|
|
|
-2 |
7 |
|
|
11157,564 |
16643,202 |
|
||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
282 |
27 |
10,6 |
446,236 |
451,073 |
18,135 |
451,071 |
18,142 |
|
|
|
||||||||||||||||||||||||||||||
|
6 |
198 |
15 |
51,0 |
198 |
15 |
53,3 |
|
|
|
|
-2 |
6 |
|
|
11608,634 |
16661,344 |
|
||||||||||||||||||||||||||||||
|
|
|
|
3 |
|
|
|
300 |
43 |
3,9 |
412,821 |
387,769 |
119,755 |
387,767 |
119,761 |
|
|
|
||||||||||||||||||||||||||||||
|
7 |
174 |
47 |
49,0 |
174 |
47 |
51,3 |
|
|
|
|
-2 |
6 |
|
|
11996,402 |
16781,105 |
|
||||||||||||||||||||||||||||||
|
|
|
|
3 |
|
|
|
295 |
30 |
55,2 |
431,886 |
402,910 |
143,063 |
402,908 |
143,069 |
|
|
|
||||||||||||||||||||||||||||||
|
8 |
166 |
16 |
13,0 |
166 |
16 |
15,3 |
|
|
|
|
-2 |
6 |
|
|
12399,310 |
16924,174 |
|
||||||||||||||||||||||||||||||
|
|
|
|
3 |
|
|
|
281 |
47 |
10,4 |
412,875 |
432,936 |
-2,234 |
432,934 |
-2,227 |
|
|
|
||||||||||||||||||||||||||||||
|
9 |
188 |
31 |
14,0 |
188 |
31 |
16,3 |
|
|
|
|
-2 |
6 |
|
|
12832,244 |
16921,947 |
|
||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
290 |
18 |
26,7 |
406,933 |
392,733 |
121,337 |
392,732 |
121,343 |
|
|
|
||||||||||||||||||||||||||||||
|
В |
279 |
41 |
40,0 |
279 |
41 |
42,2 |
|
|
|
|
|
|
|
|
13224,976 |
17043,290 |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
210 |
00 |
04 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
Г |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
1411 |
46 |
3,0 |
|
P = [S] = |
2523,807 |
м |
|
2462,257 |
м |
|
|
267,653 |
м |
|
||||||||||||||||||||||||||||||||
|
|
1411 |
46 |
8,6 |
|
|
|
|
|
|
|
2462,246 |
м |
|
|
267,691 |
м |
|
||||||||||||||||||||||||||||||
|
- |
0 |
0 |
5,60 |
|
|
|
|
|
|
|
0,011 |
м |
|
|
-0,037 |
м |
|
||||||||||||||||||||||||||||||
|
± |
0 |
0 |
13,23 |
|
|
|
|
|
|
|
0,039 |
м |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1/65200 |
|
|
||||||||||||||||||||||||||||||||
Відомість вирахування координат точок полігонометричних ходів 4 класу |
||||||||||||||||||||||||||||||||||||||||||||||||
№ |
Виміряні кути β |
Виправлені кути β |
Дирекційні кути α |
Довжини ліній S, м |
Прирости координат, м |
Координати, м |
||||||||||||||||||||||||||||||||||||||||||
Виміряні |
Виправлені |
|||||||||||||||||||||||||||||||||||||||||||||||
∆Χ |
∆Υ |
∆Χ |
∆Υ |
Χ |
Υ |
|||||||||||||||||||||||||||||||||||||||||||
Хід 3 |
||||||||||||||||||||||||||||||||||||||||||||||||
Є |
° |
′ |
″ |
° |
′ |
″ |
° |
′ |
″ |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
0,5 |
|
|
|
175 |
27 |
44,3 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
Ж |
199 |
17 |
55,0 |
199 |
17 |
54,5 |
|
|
|
|
0 |
-9 |
|
|
16347,946 |
17878,990 |
||||||||||||||||||||||||||||||||
|
|
|
0,5 |
|
|
|
197 |
11 |
38,8 |
485,963 |
-462,852 |
-143,224 |
-462,852 |
-143,234 |
|
|
||||||||||||||||||||||||||||||||
10 |
172 |
56 |
20,0 |
172 |
56 |
1,5 |
|
|
|
|
0 |
-10 |
|
|
15885,094 |
17735,756 |
||||||||||||||||||||||||||||||||
|
|
|
0,5 |
|
|
|
183 |
8 |
40,3 |
497,631 |
-507,246 |
-27,867 |
-507,246 |
-27,877 |
|
|
||||||||||||||||||||||||||||||||
11 |
192 |
14 |
29,0 |
192 |
14 |
30,5 |
|
|
|
|
0 |
-9 |
|
|
15377,849 |
17707,880 |
||||||||||||||||||||||||||||||||
|
|
|
0,5 |
|
|
|
205 |
5 |
10,8 |
471,668 |
-428,865 |
-200,770 |
-428,864 |
-200,779 |
|
|
||||||||||||||||||||||||||||||||
12 |
174 |
57 |
59,0 |
174 |
57 |
27,5 |
|
|
|
|
0 |
-9 |
|
|
14948,984 |
17507,101 |
||||||||||||||||||||||||||||||||
|
|
|
0,5 |
|
|
|
194 |
36 |
38,4 |
473,704 |
-458,595 |
-119,546 |
-458,595 |
-119,555 |
|
|
||||||||||||||||||||||||||||||||
13 |
177 |
47 |
55,0 |
177 |
47 |
1,5 |
|
|
|
|
0 |
-9 |
|
|
14490,389 |
17387,545 |
||||||||||||||||||||||||||||||||
|
|
|
0,5 |
|
|
|
190 |
37 |
39,9 |
453,761 |
-467,270 |
-87,681 |
-467,269 |
-87,690 |
|
|
||||||||||||||||||||||||||||||||
14 |
191 |
11 |
38,0 |
191 |
11 |
52,5 |
|
|
|
|
0 |
-8 |
|
|
14023,120 |
17299,855 |
||||||||||||||||||||||||||||||||
|
|
|
0,5 |
|
|
|
205 |
20 |
32,4 |
468,907 |
-366,006 |
-173,341 |
-366,006 |
-173,349 |
|
|
||||||||||||||||||||||||||||||||
15 |
166 |
48 |
26,0 |
166 |
48 |
23,5 |
|
|
|
|
0 |
-8 |
|
|
13657,113 |
17126,506 |
||||||||||||||||||||||||||||||||
|
|
|
0,5 |
|
|
|
190 |
53 |
55,9 |
394,113 |
-432,138 |
-83,208 |
-432,138 |
-83,216 |
|
|
||||||||||||||||||||||||||||||||
В |
99 |
18 |
9,0 |
99 |
18 |
2,5 |
|
|
|
|
|
|
|
|
13224,976 |
17043,290 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
191 |
57 |
07 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
Г |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
1374 |
32 |
10,00 |
|
P = [S] = |
3245,747 |
м |
|
-3122,972 |
м |
|
|
-835,638 |
м |
||||||||||||||||||||||||||||||||||
|
1374 |
32 |
14,12 |
|
|
|
|
|
|
|
-3122,970 |
м |
|
|
-835,700 |
м |
||||||||||||||||||||||||||||||||
+ |
0 |
0 |
4,12 |
|
|
|
|
|
|
|
-0,002 |
м |
|
|
0,062 |
м |
||||||||||||||||||||||||||||||||
± |
0 |
0 |
14,14 |
|
|
|
|
|
|
|
0,062 |
м |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1/52500 |
|
||||||||||||||||||||||||||||||||||
Відомість вирахування координат точок полігонометричних ходів 4 класу |
||||||||||||||||||||||||||||||||||
№ |
Виміряні кути β |
Виправлені кути β |
Дирекційні кути α |
Довжини ліній S, м |
Прирости координат, м |
Координати, м |
||||||||||||||||||||||||||||
Виміряні |
Виправлені |
|||||||||||||||||||||||||||||||||
∆Χ |
∆Υ |
∆Χ |
∆Υ |
Χ |
Υ |
|||||||||||||||||||||||||||||
Хід 4 |
||||||||||||||||||||||||||||||||||
К |
° |
′ |
″ |
° |
′ |
″ |
° |
′ |
″ |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
-1,5 |
|
|
|
160 |
37 |
02 |
|
|
|
|
|
|
|
||||||||||||||||||
П |
227 |
27 |
40,0 |
227 |
27 |
7,5 |
|
|
|
|
5 |
3 |
|
|
15803,160 |
13465,373 |
||||||||||||||||||
|
|
|
-1,5 |
|
|
|
147 |
53 |
5,5 |
515,095 |
-443,694 |
278,492 |
-443,689 |
278,495 |
|
|
||||||||||||||||||
16 |
195 |
57 |
46,0 |
195 |
57 |
17,5 |
|
|
|
|
5 |
3 |
|
|
15359,471 |
13743,868 |
||||||||||||||||||
|
|
|
-1,5 |
|
|
|
157 |
25 |
22,9 |
503,955 |
-468,908 |
194,966 |
-468,903 |
194,970 |
|
|
||||||||||||||||||
17 |
166 |
20 |
38,0 |
166 |
20 |
43,5 |
|
|
|
|
5 |
3 |
|
|
14890,569 |
13938,838 |
||||||||||||||||||
|
|
|
-1,5 |
|
|
|
148 |
17 |
6,4 |
509,859 |
-444,034 |
274,401 |
-444,029 |
274,404 |
|
|
||||||||||||||||||
18 |
169 |
31 |
43,0 |
169 |
31 |
23,5 |
|
|
|
|
5 |
3 |
|
|
14446,539 |
14213,242 |
||||||||||||||||||
|
|
|
-1,5 |
|
|
|
147 |
11 |
29,9 |
511,185 |
-415,583 |
267,911 |
-415,578 |
267,914 |
|
|
||||||||||||||||||
19 |
203 |
07 |
50,0 |
203 |
07 |
57,5 |
|
|
|
|
5 |
3 |
|
|
14030,961 |
14481,156 |
||||||||||||||||||
|
|
|
-1,5 |
|
|
|
161 |
50 |
27,4 |
493,326 |
-451,950 |
148,236 |
-451,945 |
148,239 |
|
|
||||||||||||||||||
20 |
174 |
42 |
3,0 |
174 |
42 |
35,5 |
|
|
|
|
5 |
3 |
|
|
13579,016 |
14629,395 |
||||||||||||||||||
|
|
|
-1,5 |
|
|
|
153 |
27 |
2,8 |
503,994 |
-441,060 |
220,378 |
-441,055 |
220,381 |
|
|
||||||||||||||||||
Б |
295 |
26 |
17,0 |
295 |
26 |
57,5 |
|
|
|
|
|
|
|
|
13137,961 |
14849,776 |
||||||||||||||||||
|
|
|
|
|
|
|
191 |
57 |
07 |
|
|
|
|
|
|
|
||||||||||||||||||
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
1432 |
34 |
13,00 |
|
P = [S] = |
3016,803 |
м |
|
-2665,229 |
м |
|
|
1384,383 |
м |
||||||||||||||||||||
|
1432 |
34 |
2,31 |
|
|
|
|
|
|
|
-2665,199 |
м |
|
|
1384,403 |
м |
||||||||||||||||||
+ |
0 |
0 |
10,69 |
|
|
|
|
|
|
|
-0,029 |
м |
|
|
-0,020 |
м |
||||||||||||||||||
± |
0 |
0 |
13,23 |
|
|
|
|
|
|
|
0,035 |
м |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
85800 |
|
||||||||||||||||||||
Відомість вирахування координат точок полігонометричних ходів 4 класу |
|||||||||||||||||||||||||
№ |
Виміряні кути β |
Виправлені кути β |
Дирекційні кути α |
Довжини ліній S, м |
Прирости координат, м |
Координати, м |
|||||||||||||||||||
Виміряні |
Виправлені |
||||||||||||||||||||||||
∆Χ |
∆Υ |
∆Χ |
∆Υ |
Χ |
Υ |
||||||||||||||||||||
Хід 5 |
|||||||||||||||||||||||||
Л |
° |
′ |
″ |
° |
′ |
″ |
° |
′ |
″ |
|
|
|
|
|
|
|
|||||||||
|
|
|
0,2 |
|
|
|
93 |
36 |
50,6 |
|
|
|
|
|
|
|
|||||||||
М |
148 |
45 |
0,0 |
148 |
45 |
0,2 |
|
|
|
|
-3 |
-1 |
|
|
10724,493 |
12645,119 |
|||||||||
|
|
|
0,2 |
|
|
|
62 |
21 |
50,8 |
452,155 |
209,733 |
400,570 |
209,730 |
400,569 |
|
|
|||||||||
21 |
178 |
54 |
8,0 |
178 |
54 |
8,2 |
|
|
|
|
-3 |
-1 |
|
|
10934,223 |
13045,688 |
|||||||||
|
|
|
0,2 |
|
|
|
61 |
15 |
59,0 |
494,784 |
237,861 |
433,858 |
237,858 |
433,858 |
|
|
|||||||||
22 |
169 |
47 |
44,0 |
169 |
47 |
44,2 |
|
|
|
|
-3 |
-1 |
|
|
11172,081 |
13479,546 |
|||||||||
|
|
|
0,2 |
|
|
|
51 |
3 |
43,2 |
460,341 |
289,315 |
358,065 |
289,312 |
358,065 |
|
|
|||||||||
23 |
164 |
30 |
21,0 |
164 |
30 |
21,2 |
|
|
|
|
-3 |
-1 |
|
|
11461,393 |
13837,611 |
|||||||||
|
|
|
0,2 |
|
|
|
35 |
34 |
4,4 |
501,479 |
407,916 |
291,694 |
407,913 |
291,693 |
|
|
|||||||||
24 |
188 |
55 |
0,0 |
188 |
55 |
0,2 |
|
|
|
|
-3 |
-1 |
|
|
11869,306 |
14129,304 |
|||||||||
|
|
|
0,2 |
|
|
|
44 |
29 |
4,7 |
516,770 |
368,684 |
362,110 |
368,680 |
362,109 |
|
|
|||||||||
25 |
161 |
59 |
43,0 |
161 |
59 |
43,2 |
|
|
|
|
-3 |
-1 |
|
|
12237,986 |
14491,413 |
|||||||||
|
|
|
0,2 |
|
|
|
26 |
28 |
47,9 |
496,351 |
444,279 |
221,315 |
444,276 |
221,315 |
|
|
|||||||||
26 |
170 |
15 |
30,0 |
170 |
15 |
30,2 |
|
|
|
|
-3 |
-1 |
|
|
12682,262 |
14712,727 |
|||||||||
|
|
|
0,2 |
|
|
|
16 |
44 |
18,1 |
475,864 |
455,702 |
137,050 |
455,699 |
137,049 |
|
|
|||||||||
Б |
75 |
12 |
42,0 |
75 |
12 |
42,2 |
|
|
|
|
|
|
|
|
13137,961 |
14849,776 |
|||||||||
|
|
|
|
|
|
|
271 |
57 |
0,3 |
|
|
|
|
|
|
|
|||||||||
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
1258 |
20 |
8,0 |
|
P = [S] = |
3397,744 |
м |
|
2413,489 |
м |
|
|
2204,663 |
м |
|||||||||||
|
1258 |
20 |
9,7 |
|
|
|
|
|
|
|
2413,468 |
м |
|
|
2204,657 |
м |
|||||||||
- |
0 |
0 |
1,74 |
|
|
|
|
|
|
|
0,022 |
м |
|
|
0,006 |
м |
|||||||||
азва вузлового напрямку |
№ хо-ду |
Назва вихід-них дирек-ційних кутів |
Значення вихідних дирекційних кутів |
Сума виміряних кутів Σβ |
Число кутів n+1 |
Вага |
Наближення |
v″ |
pv |
pv² |
||||||||||||||||||||||||||||||||||||||
І |
ІІ |
ІІІ |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
° |
′ |
″ |
° |
′ |
″ |
° |
′ |
″ |
|
|
|
|||||||||||||||||||||||||||||||||||||
Б-А |
1 |
Г-В |
- |
1098 |
02 |
48 |
6 |
1,67 |
- |
11 |
57 |
16 |
11 |
57 |
16 |
-9 |
-15 |
135,3 |
||||||||||||||||||||||||||||||
4 |
К-П |
160 |
37 |
02 |
1432 |
33 |
57 |
7 |
1,43 |
11 |
56 |
55 |
11 |
56 |
55 |
11 |
56 |
55 |
+12 |
+17,2 |
205,9 |
|||||||||||||||||||||||||||
5 |
Л-М |
166 |
23 |
10 |
1258 |
20 |
20 |
8 |
1,25 |
11 |
57 |
10 |
11 |
57 |
10 |
11 |
57 |
10 |
-3 |
-3,8 |
11,3 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4,35 |
11 |
57 |
02 |
11 |
57 |
07 |
11 |
57 |
07 |
|
-1,6 |
352,5 |
||||||||||||||||||||||||||
В-Г |
1 |
А-Б |
- |
1098 |
02 |
48 |
6 |
1,67 |
209 |
59 |
57 |
209 |
59 |
55 |
209 |
59 |
56 |
+8 |
+11,7 |
81,8 |
||||||||||||||||||||||||||||
2 |
Д-Е |
238 |
13 |
50 |
1411 |
46 |
30 |
7 |
1,43 |
210 |
00 |
20 |
210 |
00 |
20 |
210 |
00 |
20 |
-16 |
-24,3 |
413,3 |
|||||||||||||||||||||||||||
3 |
Є-Ж |
185 |
27 |
44 |
1374 |
32 |
11 |
8 |
1,25 |
209 |
59 |
55 |
209 |
59 |
55 |
209 |
59 |
55 |
+9 |
+10 |
80,0 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4,35 |
210 |
00 |
04 |
210 |
00 |
03 |
210 |
00 |
04 |
|
-2,6 |
575,1 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[pv²]= |
927,6 |
||||||||||||||||||||||||||
Зрівноваження абсцис вузлових точок полігонометричної мережі 4 класу способом послідовних наближень |
||||||||||||||
Назва вузла |
№ хо-ду |
Назва вихідних пунктів |
Значення абсцис вихід-них пунктів |
Сума виміря-них приростів |
Число сторін ходу |
Вага |
Наближення |
vx |
pv |
pv² |
||||
І |
ІІ |
ІІІ |
ІV |
V |
||||||||||
Б |
1 |
В |
- |
87,006 |
5 |
0,20 |
- |
13137,967 |
13137,969 |
13137,969 |
13137,969 |
-9 |
-1,80 |
16,20 |
4 |
П |
15113,241 |
-2665,229 |
6 |
0,17 |
13137,931 |
13137,931 |
13137,931 |
13137,931 |
13137,931 |
29 |
4,83 |
140,17 |
|
5 |
М |
10254,167 |
2413,489 |
7 |
0,14 |
13137,982 |
13137,982 |
13137,982 |
13137,982 |
13137,982 |
-22 |
-3,14 |
69,14 |
|
|
|
|
|
|
|
0,51 |
13137,955 |
13137,960 |
13137,961 |
13137,961 |
13137,960 |
|
-0,11 |
225,51 |
В |
1 |
Б |
- |
87,006 |
5 |
0,20 |
13224,961 |
13224,966 |
13224,967 |
13224,967 |
13224,967 |
8 |
1,60 |
- |
2 |
Е |
9574,572 |
2462,257 |
6 |
0,17 |
13224,987 |
13224,987 |
13224,987 |
13224,987 |
13224,987 |
-12 |
-2,00 |
24,00 |
|
3 |
Ж |
14883,334 |
-3122,972 |
7 |
0,14 |
13224,974 |
13224,974 |
13224,974 |
13224,974 |
13224,974 |
1 |
0,14 |
0,14 |
|
|
|
|
|
|
|
0,51 |
13224,973 |
13224,975 |
13224,976 |
13224,975 |
13224,975 |
|
-0,26 |
24,14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
[pv²]= |
249,65 |
Зрівноваження ординат вузлових точок полігонометричної мережі 4 класу способом послідовних наближень |
|||||||||||||
Назва вузла |
№ хо-ду |
Назва вихідних пунктів |
Значення абсцис вихід-них пунктів |
Сума виміря-них приростів |
Число сторін ходу |
Вага |
Наближення |
vy |
pv |
pv² |
|||
І |
ІІ |
ІІІ |
ІV |
||||||||||
Б |
1 |
В |
- |
2193,502 |
5 |
0,20 |
- |
14849,785 |
14849,788 |
14849,788 |
-13 |
-2,60 |
33,80 |
4 |
П |
13465,373 |
1384,383 |
6 |
0,17 |
14849,756 |
14849,756 |
14849,756 |
14849,756 |
19 |
3,17 |
60,17 |
|
5 |
М |
12645,119 |
2204,663 |
7 |
0,14 |
14849,782 |
14849,782 |
14849,782 |
14849,782 |
-6 |
-0,86 |
5,14 |
|
|
|
|
|
|
|
0,51 |
14849,768 |
14849,775 |
14849,776 |
14849,776 |
|
-0,29 |
99,11 |
В |
1 |
Б |
- |
2193,502 |
5 |
0,20 |
17043,270 |
17043,277 |
17043,277 |
|
13 |
2,60 |
- |
2 |
Е |
16775,599 |
267,653 |
6 |
0,17 |
17043,252 |
17043,252 |
17043,252 |
37 |
6,17 |
228,17 |
||
3 |
Ж |
17878,990 |
-835,638 |
7 |
0,14 |
17043,352 |
17043,352 |
17043,352 |
-62 |
-8,86 |
549,14 |
||
|
|
|
|
|
|
0,51 |
17043,287 |
17043,290 |
17043,290 |
|
-0,09 |
777,31 |
|
|
|
|
|
|
|
|
|
|
|
|
|
[pv²]= |
876,42 |
Оцінка точності польових вимірів та зрівноважених значень дирекційних кутів вузлових напрямків:
СКП одиниці ваги
та
її надійність
визначення ваг дирекційних кутів
та
:
визначення СКП зрівноважених значень дирекційних кутів та :
оцінка надійності СКП зрівноважених значень дирекційних кутів та :
Оцінка точності координат вузлових точок.
СКП одиниці ваг
,
та їх надійності
,
:
визначення ваг зрівноважених координат вузлових точок Б та В:
визначення СКП зрівноважених координат вузлових точок Б та В:
оцінка надійності СКП зрівноважених значень координат вузлових точок Б та В:
СКП положення вузлових точок:
