4.2 Зрівноваження полігонометричного ходу способом найменших квадратів. Теоретичні відомості зрівноваження поліго- нометричного ходу способом найменших квадратів

Першою задачею у зрівноваженні одиноких ходів є одночасне виконання трьох умов, яким повинні відповідати дирекційні кути, прирости абсцис та ординат полігону. Отже, потрібно вибрати найбільш раціональний спосіб зрівноваження.

Зрівноваження одинокого полігонометричного ходу зручно виконувати способом умовних вимірювань (корелатним), тому що безпосередньо виміряних величин в полігонометричному ході завжди на три більше, ніж необхідних, тому кількість умовних рівнянь рівна трьом.

Можна скласти три умовні рівняння:

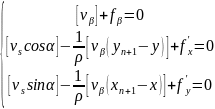(4.19)

де 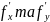- нев’язки в сумах приростів абсцис і ординат при обчисленні ходу без попереднього виправлення кутів.

Обчисливши первинну поправку в кут:

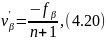
Виправляють кути і, обчисливши нові прирости координат, замість отримують нові значення нев’язок .

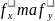Для обчислення величин 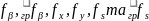використовують відповідні формули:

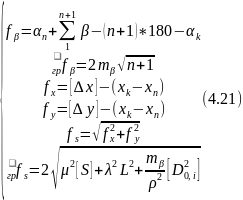
Для спрощення обчислень застосовують двогрупове зрівноваження (коли порередньо зрівноважуються виміряні кути); при цьому початок координат пнреносять в центр тяжіння ходу.

Виконовши попереднє зрівноваження виміряних кутів,обчисливши за ними значення дирекцій них кутів та взявши за початок координат першу точку ходу, знаходять з точністю до 1 м координати, які називають умовними,за формулами

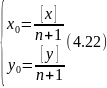
а також центральні координати пунктів ходу:

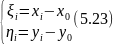
оскільки 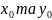- це координати центру ваги вершин полігонометричного ходу,то

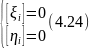
Ці рівності повинні бути дотримані в межах 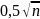одиниць останнього знаку, де n- число доданків. Такі вимоги висувають й до інших конрольних формул увигляді суми. У відповідності з введеними позначеннями умовні рівняння для полігонометричного ходу матимуть вигляд:

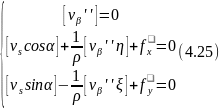
де 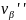- вторинна поправка у виміряний кут.

Вважаючи що кути виміряні за однакових умов, можна записати:

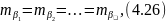
Отже,

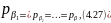
де

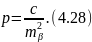
Коефіцієнти нормальних рівнянь корелат будуть мати вигляд:

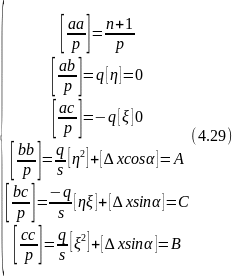
Отримавши корелати,обчислюють поправки в кути та лінії:

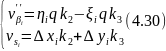
Обцислені значення поправок контролюють за формулами:

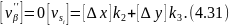
Далі знаходять поправки в дирекційні кути за формулою:

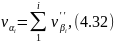
а потім обчислюють поправки в прирости координат за диференціальними формулами:

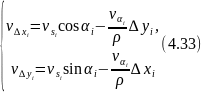
Для заключного контролю потрібно, щоб виконувались наступні умови:

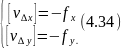
Відсутність нев’зок в приростах координат при повторному обчислені ходу буде слугвати заключним контролем! Необхідна кількість знаків при обчисленні зберігається відновідно до загальноприйнятих у способі найменших квадратів і геодезії правил.

Розділ 5 Зрівноваження витягнутого полігонометричного ходу 4 класу корелатним способом

Виконання зрівноваження полігонометричного ходу корелатним способом , виконується в такій послідовності:

• Записуються виміряні кути та довжини сторін

• Визначається довжина ходу S :

S = S1+S2+S3...

• Визначається кутова нев’язка ходу f_ = ∑ пр + ∑т і порівнюється з допустимою 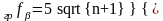, де n – кількість ліній в ході. Первинні поправки в кути (ліквідовують кутову нев’язку) визначаються за формулою .

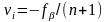• За виміряними кутами з врахуванням первинних поправок, вираховуються дирекційні кути.

• Знаходимо наближені прирости координат за формулами:

x1=соsS1 (5.1)

y1=sinS1

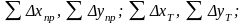
• Потім обчислюються величини 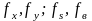. Відносна нев’язка має бути меншою за 1:25000 (для 4 класу).

• Обчислюємо наближені абсциси X’, які утворюються шляхом додавання довжини ліній, заокруглених до цілих метрів. Абсцису центру ваги ходу обчислюють за формулою :

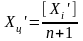. (5.2)

• Абсциси точок ходу відносно центру ваги, вираховуються за формулою

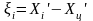. (5.3)

• Далі, за межами таблиці, знаходять поздовжній та поперечний зсуви t та u за формулами:

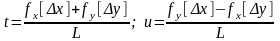; (5.4)

контроль: 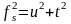_(5.5)

• Зрівноважені значення довжин сторін обчислюють шляхом додавання до виміряних довжин поправок , які вираховуються за формулою (е визначається до 7 знаку після коми):

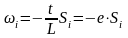; (5.6)

• Вираховуємо.вторинні поправки у виміряні кути за формулою (k обчислюється до 7 знаку після коми):

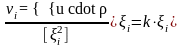(5.7)

Їх сума повинна дорівнювати 0. Вторинні поправки записуються під виміряними кутами червоним кольором.

• Визначаємо поправки в дирекційні кути за формулою:

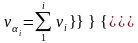_(5.8)

• За зрівноваженими значеннями дирекційних кутів та довжин ліній, обчислюються зрівноважені прирости

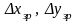
• За зрівноваженими приростами визначаються кінцеві значення координат X, Y. Контроль: вирахувані значення кінцевих координат повинні точно співпасти з виписаними.

Строге зрівноваження полігонометричного ходу здійснено у таблиці 5.1