Висновки до розділу

Проектування планово-висотного обґрунтування для кадастрового зні- мання в масштабі 1:2000 включає проектування полігонометричних ходів, засі- чок для планової та нівелірних ходів для висотної прив’язки планово-висотних опознаків, а головне перевірку ряду вимог (відповідність характеристик, критері- їв ходів і засічок галузевій інструкції для знімання місцевості, встановлення фо- рми ходів і засічок, спостереження взаємної видимість пунктів, оцінка точності), згідно яких потрібно запроектувати ходи. Також важливим чинником проекту- вання є вибір оптимального приладу для виконання робіт заданої точності (не тільки вимірювання кутів та ліній, а й похибок центрування, редукції тощо).

Для ефективнішого проектування планово-висотного обґрунтування у да- ній роботі складено два варіанти для виявлення переваг та недоліків у кожному з варіантів (додаток 1, додаток 2).

Розділ 4 Зрівноваження мережі полігонометричних ходів IV класу способом послідовних наближень. Зрівноваження полігонометричних ходів способом найменших квадратів

1. Зрівноваження мережі полігонометричних ходів IV класу способом послідовних наближень

   1. Побудова схеми мережі полігонометричних ходів за вихід- ними даними. Розрахунок та побудова укрупненої схеми мережі

Схему мережі полігонометричних ходів будують так (рис. 5.1):

1. Складають саму схему, де підписують назви (номери) всіх пунктів (точок), а також номери ходів;

2. У вузлах відображають фіктивні напрями, назви кінців яких утворю- ються, як правило, із назв вузлових пунктів з додаванням букви а. Напрям утво- рюється шляхом додавання до всіх кутів вузла будь-якої кількості градусів, яка не рівна жодному виміряному куту вузла;

3. Виписують виміряні кути та довжини ліній (горизонтальні прокладен-

ня).

На укрупненій схемі мережі вказують:

1. Назви (номери) вихідних та вузлових пунктів (точок) та напрямів;

2. В стовпчик записують такі дані: номер ходу, сума виміряних прирос-

тів, нев’язки, довжина ходу, кількість кутів;

3. Стрілки, що показують напрями ходів (як правило, від вихідних до ву- злових точок).

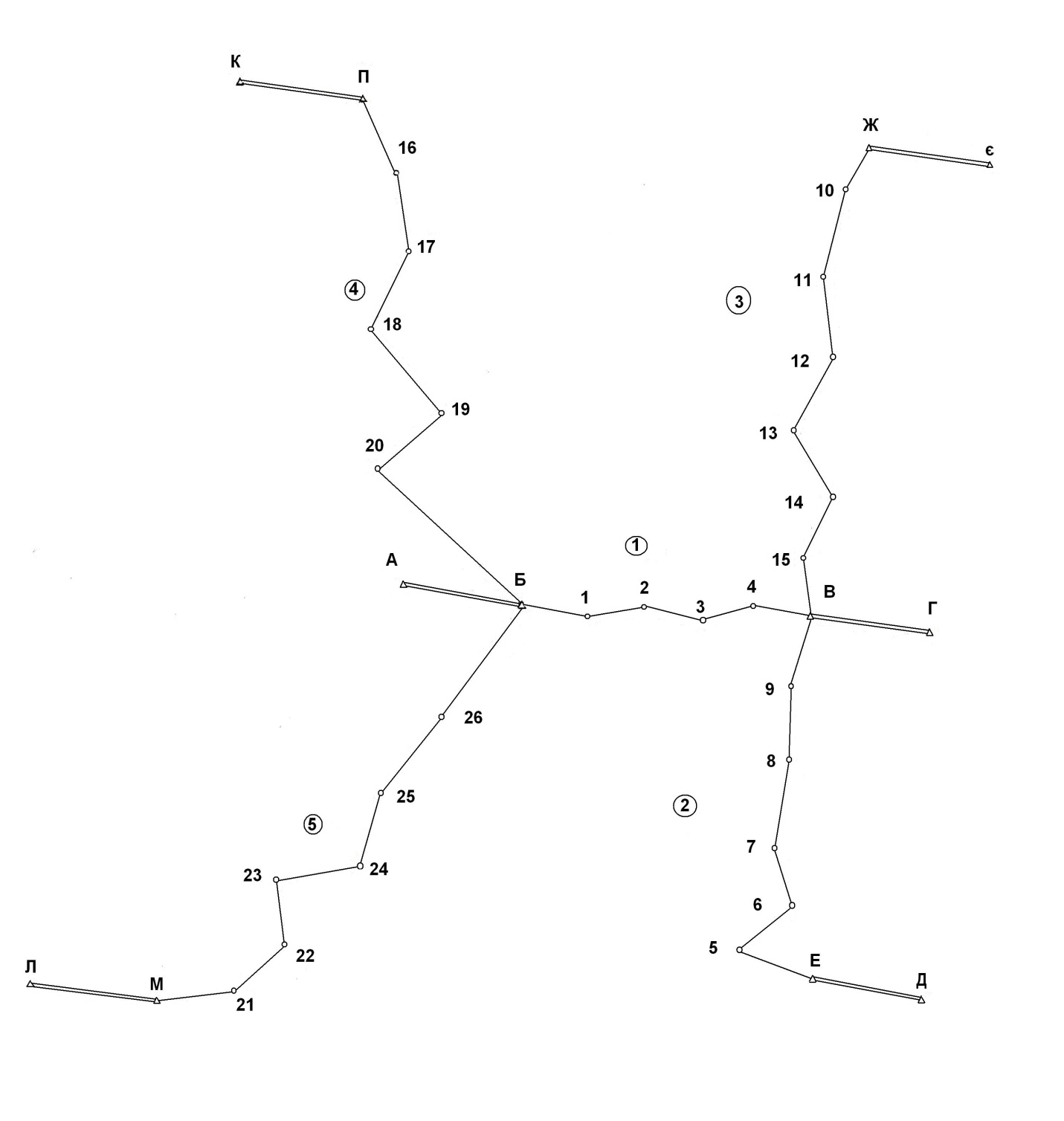
Рис. 4.1 Схема мережі полігонометричних ходів 4 класу

4.1.2 Зрівноваження мережі та оцінка точності отриманих результатів Роздільне зрівноваження мережі полігон

ометричних ходів можна проводити способами: еквівалентної заміни, послідовних наближень (вузлів), способом полігонів В. В. Попова. Цими способами спочатку отримують дирекційні кути вузлових напрямків і координати вузлових пунктів, а потім, використовуючи їх як вихідні, зрівноважують окремі ходи також нестрогим способом, розподіляючи нев’язки в прирости координат прямо пропорційно до числа ліній (при вимірюванні світловіддалеміром) або до довжин ліній (при вимірюванні дротами).

Зрівноважити мережу полігонометричних ходів 4 класу, що спираються на пункти тріангуляції та провести оцінку точності кінцевих значень дирекційних кутів вузлових напрямків і координат вузлових точок. Укрупнена схема мережі полігонометричних ходів 4 класу показана на рис. 4.2.

Для визначення граничної кутової нев’язки прийнята середня квадратична помилка вимірювання кута .

Приклад зрівноваження наведено в табл. 4.2, 4.3, 4.4 та 4.5

Обчислення починають із визначення дирекційних кутів вихідних напрямків. За координатами вихідних пунктів знаходимо румби:

Дирекційний кут напрямку 12 вираховується за румбом з врахуванням чверті, в якій він знаходиться, а чверть визначається за знаками приростів координат (ΔX; ΔY), (табл. 4.1)

Таблиця 4.1- Визначення дирекцій них кутів

Чверть	Знаки приростів	Формули
І
ІІ
ІІІ
ІV

Далі вираховують суми кутів в кожному ході (табл.4.2). Після цього способом послідовних наближень зрівноважують дирекційні кути вузлових напрямків Б-А та В-Г (табл.5.3) в такій послідовності.

Спочатку заповнюють графи 1-6 табл.5.3. В графу 1 записують назви вузлових напрямків, в графу 2 – номера ходів, що сходяться у даному вузлі. В графу 3 виписують із схеми назви вихідних дирекційних кутів, а в графу 4 – їхні значення, вирахувані за координатами вихідних точок. В графу 5 виписують із табл.5.2 суми виміряних кутів, а в графу 6 – їх кількість. Потім вираховують вагу кожного ходу за формулою (5.2) і записують в графу 7.

де с – константа (приймається рівною одиниці);

n+1 – число кутів.

Значення дирекційного кута вузлового напрямку Б-А отримують двічі з ходів 4 та 5, використовуючи формулу (для випадку виміряних лівих кутів):

Перше наближення дирекційного кута Б–А отримують як середнє вагове із значень, вирахуваних з ходів 4 та 5. Перше наближення дирекційного кута В–Г отримують як середнє вагове із значень, вирахуваних з ходів 1, 2, 3. Слід пам’ятати, що для вирахування дирекційного кута В–Г з ходу 1 використовується не кут Б–А, отриманий в першому наближенні, а зворотній йому А–Б, вирахуваний за формулою:

Після виконання першого наближення переходять до другого, вираховуючи дирекційні кути вузлових напрямків в тій самій послідовності. За вихідні при кожному наступному вирахуванні приймають значення дирекційних кутів, отриманих з попередніх наближень.

Друге наближення дирекційного кута Б–А отримують вже як середнє вагове із значень, вирахуваних із ходів 1, 4, 5. Слід мати на увазі, що при вирахуванні в другому та наступних наближеннях дирекційного кута Б–А з ходу 1, напрямок ходу змінюється на протилежний, отже виміряні кути β будуть правими і дирекційний кут буде вираховуватись за формулою:

Крім цього, в даному ході, як і у вищезгаданому випадку, вирахуваний в попередньому наближенні дирекційний кут В–Г замінюється на зворотній Г–В. Вирахування закінчують, коли значення двох останніх наближень не будуть відрізнятись між собою.

Після вирахування кінцевих значень дирекційних кутів визначають поправки на кожен хід як різницю між кінцевим значенням і отриманим з і-го ходу в останньому наближенні.

Вирахування поправок контролюється співвідношенням

або при наявності помилок заокруглення

де β – гранична помилка заокруглення величини середнього вагового значення дирекційного кута та поправок.

Отримавши зрівноважені значення дирекційних кутів вузлових напрямків можна переходити до зрівноваження координат вузлових точок. Для цього необхідно мати практичні суми приростів ходів, які вираховують у відомості вирахування полігонометричних ходів (табл.). Зрівноваження координат вузлових точок виконують способом послідовних наближень окремо для абсцис та ординат. Зрівноваження виконують в такій послідовності. Заповнюють графи 1-6 таблиці 19. Далі вираховують ваги суми приростів по кожному ходу за формулою

де с – константа; n – число сторін в ході.

Формулу (5.9) використовують при вимірюванні ліній світловіддалеміром. Вирахувані ваги записують в графі 7. Значення абсциси вузлової точки Б в першому наближенні вираховують з ходів 4 і 5 за формулою

Значення абсциси вузлової точки В в першому наближенні вираховують з ходів 1, 2 та 3, використовуючи для першого ходу абсцису точки Б, отриману в першому наближенні. Після виконання першого наближення переходять до другого, вираховуючи абсциси вузлових точок в тій самій послідовності. За вихідні при кожному наступному вирахуванні приймають значення абсцис, отриманих з попередніх наближень. Закінчують вирахування тоді, коли значення двох останніх наближень не будуть відрізнятись між собою.

Після вирахування кінцевих значень абсцис визначають поправки на кожен хід як різницю між кінцевим значенням абсциси і отриманим по ходу в останньому наближенні.

Зрівноваження ординат вузлових точок Б і В виконують аналогічно до зрівноваження абсцис (табл.5.4). Отримавши зрівноважені значення координат вузлових точок їх записують у відомості вирахування полігонометричних ходів (табл.5.2). Далі знаходять теоретичну суму приростів, вираховують нев’язки та вводять поправки у виміряні прирости. В результаті отримують виправлені прирости і розраховують координати усіх точок полігонометричних ходів. При розрахунку відносної нев’язки полігонометричного ходу f_відн, отримані значення в знаменнику заокруглюються до сотень завжди в меншу сторону.

Після зрівноваження мережі полігонометричних ходів виконують оцінку точності.

Оцінку точності зрівноважених значень дирекційних кутів, абсцис або ординат виконують за формулою:

Середньоквадратичну похибку (СКП) одиниці ваги для напрямків або приростів визначають за формулою:

де n– кількість всіх ходів,

k – кількість вузлових точок.

Надійність величин μ та M визначають за формулами:

Для оцінки точності зрівноважених значень використовуютьзначенняваг вузлових точок або напрямків, які обчислюють заформулою В. Козлова.

Розрахунки виконують у двох наближеннях.

З першого наближення

де – сума ваг ходів, які сходяться в точці i;

– вага окремих ходів, які є зв’язуючими міжточкою і та сусідніми вузловими точками a,b,…,k;

– суми ваг ходів, які сходяться у вузлових точках, з якими точка і має зв’язуючі ходи.

З другого наближення

де – ваги вузлових напрямків (точок) a, b,…,k, зякими вузлова точка і має зв’язуючі ходи, вирахувані в першомунаближенні.

Оцінку точності координат вузлових точок виконують окремо для абсцис та ординат та закінчують визначенням середньоїквадратичної помилки положення вузлової точки за формулою