Фігури обертання.

Циліндр

67. Осьовий переріз циліндра – квадрат, діагональ якого 4 . Знайти площу повної поверхні та об’єм циліндра.

68. Діагональ осьового перерізу циліндра дорівнює 10 см, а кут між діагоналями осьового перерізу 120 . Знайти площу повної поверхні та об’єм циліндра.

69. Радіус основи циліндра дорівнює 3 см, а діагональ осьового перерізу утворює з площиною онови кут 60 . Знайти площу бічної поверхні та об’єм циліндра..

70. Висота циліндра дорівнює 6 см, а діагональ осьового перерізу утворює з твірною кут 60 . Знайти площу бічної поверхні та об’єм циліндра.

71. В основі циліндра проведено хорду, що стягує дугу . Відрізок, який сполучає центр іншої основи з серединою цієї хорди дорівнює і утворює з площиною основи кут . Визначте площу бічної поверхні та об’єм циліндра.

72. У нижній основі циліндра проведено хорду довжиною . ЇЇ видно з цього центра під кутом . Визначте площу бічної поверхні та об’єм циліндра, якщо відрізок, що з’єднує центр верхньої основи з серединою хорди, утворює з площиною основи кут .

73. В сонові циліндра проведено хорду , яку видно із центра цієї основи під кутом . Відстань від центра до хорди дорівнює . Відрізок, який сполучає центр однієї основи з точкою кола іншої основи, утворює з площиною основи кут . Визначте площу повної поверхні та об’єм циліндра.

74. В сонові циліндра проведено хорду , яку видно із центра цієї основи під кутом . Відстань від центра до хорди дорівнює . Відрізок, який сполучає центр однієї основи з точкою кола іншої основи, утворює з площиною основи кут . Визначте площу повної поверхні та об’єм циліндра.

75. У нижній основі циліндра проведено хорду, яка знаходиться на відстані від центра нижньої основи. ЇЇ видно з цього центра під кутом . Визначте площу повної поверхні та об’єм циліндра, якщо діагональ перерізу утворює з площиною основи кут .

76. В циліндрі проведено відрізок, що з’єднує центр верхньої основи з точкою кола нижньої основи, у утворює з нею кут . В основі проведено хорду довжиною , яка стягує дугу . Визначте площу повної поверхні та об’єм циліндра.

77. Паралельно осі циліндра проведено площину, яка перетинає основу по хорді, що стягує дугу . Визначте площу бічної поверхні та об’єм циліндра, якщо діагональ перерізу дорівнює і утворює з площиною основи кут .

78. У нижній основі циліндра проведено хорду. ЇЇ видно з цього центра під кутом . Визначте площу бічної поверхні та об’єм циліндра, якщо діагональ перерізу, що паралельний осі, дорівнює і утворює з площиною основи кут .

79. В циліндрі паралельно його осі проведено переріз, який перетинає нижню основу циліндра по хорді довжиною , яка видно з центра цієї основи під кутом _{, а з центра верхньої основи під кутом} . Визначте площу повної поверхні та об’єм циліндра.

80. Паралельно осі циліндра проведено площину, що перетинає основу по хорді, довжина якої . Ця хорда стягує дугу . Визначте площу повної поверхні та об’єм циліндра, якщо діагональ утвореного перерізу нахилена до основи під кутом .

Конус

67. Осьовим перерізом конуса є рівнобедрений трикутник з кутом 120 при вершині і бічною стороною 8 см. Знайти площу повної поверхні та об’єм конуса.

68. Осьовий переріз конуса – рівнобедрений трикутник з основою 8 см і кутом при вершині 120 . Знайти площу повної поверхні та об’єм конуса.

69. Радіус основи конусу дорівнює 6 см, а його осьовий переріз – рівнобедрений прямокутний трикутник. Знайти площу бічної поверхні та об’єм конуса.

70. Твірна конусі 14 см, кут при вершині осьового перерізу дорівнює 60 . Знайти площу бічної поверхні та об’єм конуса.

71. Переріз конуса , який проходить через його вершину, перетинає основу конуса по хорді, яку видно з центра під кутом . Площа перерізу утворює з висотою кут . Знайти площу бічної поверхні конуса та об’єм , якщо його висота дорівнює .

72. Через дві твірні конуса, кут між якими дорівнює , проведено переріз, що утворює з площиною основи конуса кут . Знайти площу бічної поверхні конуса та об’єм, якщо висота дорівнює

73. В основі конуса проведено хорду, яку видно із центра основи під кутом , а з вершини конуса – під кутом . Знайти площу повної поверхні конуса та об’єм , якщо його радіус дорівнює .

74. Через дві твірні конуса, кут між якими дорівнює , проведено переріз, який утворює з площиною основи конуса кут . Знайти площу повної поверхні конуса та об’єм , якщо його твірна дорівнює .

75. В основі конуса проведено хорду, яку видно із центра основи під кутом , а з вершини конуса – під кутом . Знайти площу бічної конуса та об’єм , якщо відрізок, який сполучає вершину конуса з серединою хорди, дорівнює .

76. В основі конуса проведено хорду, яку видно із центра основи під кутом , а з вершини конуса – під кутом . Знайти площу бічної поверхні конуса та об’єм , якщо відрізок, який сполучає вершину конуса з серединою хорди, дорівнює .

77. В основі конуса проведено хорду, яку видно із центра основи під кутом , а з вершини конуса – під кутом . Знайти площу повної поверхні конуса та об’єм , якщо його твірна дорівнює .

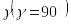78. В основі конуса проведено хорду, яку видно із центра основи під кутом . Знайти площу повної поверхні конуса та об’єм , якщо відрізок, який сполучає вершину конуса з серединою хорди, дорівнює .і утворює з площиною кут .

79. Через дві твірні конуса, кут між якими дорівнює , проведено переріз, який утворює з площиною основи конуса кут . Знайти площу бічної поверхні конуса та об’єм , якщо відстань від центра до хорди .

80. В основі конуса проведено хорду, яку видно із центра основи під кутом , а з вершини конуса – під кутом . Знайти площу бічної поверхні конуса та об’єм, хорда дорівнює .