Підготовка «Об’ємні фігури» Правильна трикутна призма
Обчислити площу повної поверхні та об’єм правильної трикутної призми, якщо діагональ бічної грані дорівнює 15 см, а висота основи дорівнює 2√3.
Обчислити площу повної поверхні та об’єм правильної трикутної призми, якщо діагональ бічної грані утворює з площиною основи кут 45
і дорівнює 6 см.Обчислити площу бічної поверхні та об’єм правильної трикутної призми, якщо діагональ бічної грані утворює з площиною основи кут 60 і дорівнює 8 см..
Обчислити площу бічної поверхні та об’єм правильної трикутної призми, якщо діагональ бічної грані утворює з площиною основи кут 30 і дорівнює 4 см..
Правильна чотирикутна призма
Обчислити площу повної поверхні та об’єм правильної чотирикутної призми, діагональ бічної грані якої дорівнює 2 см і утворює з площиною основи кут 60 .
Обчислити площу повної поверхні та об’єм правильної чотирикутної призми, якщо діагональ основи дорівнює 4 см, а діагональ призми утворює з площиною основи кут 30 .
Обчислити площу бічної поверхні та об’єм правильної чотирикутної призми, діагональ якої дорівнює 12 см і утворює з площиною основи кут 30 .
Обчислити площу бічної поверхні та об’єм правильної чотирикутної призми, діагональ якої дорівнює 24 см і утворює з площиною основи кут 60 .
У правильній чотирикутній призмі висота дорівнює
.
Діагональ призми утворює з бічним
ребром кут
.
Обчисліть площу повної поверхні та
об’єм призми.Діагональ правильної чотирикутної призми дорівнює
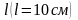і
утворює з площиною основи кут
.
Обчисліть площу бічної поверхні та
об’єм призми.
Пряма призма (прямий паралелепіпед)
Знайти площу повної поверхні та об’єм прямого паралелепіпеда , більша діагональ якого дорівнює 5 дм, а сторони основи 1 дм і 4 дм, кут між ними 60
.Знайти площу повної поверхні та об’єм прямого паралелепіпеда , менша діагональ якого дорівнює 5 дм, а сторони основи 2 дм і 3 дм, кут між ними 120 .
В основі прямого паралелепіпеда лежить паралелограм, сторони якого 8см і 12см, а тупий кут - 120 . Висота паралелепіпеда дорівнює меншій діагоналі основи. Знайти площу бічної поверхні та об’єм.
В основі прямого паралелепіпеда лежить паралелограм, сторони якого 15см і 24см, а гострий кут - 60 . Більша діагональ паралелепіпеда нахилена до площини основи під кутом 30 . Знайти площу бічної поверхні та об’єм .
Обчислити площу повної поверхні та об’єм прямої призми, основа якої ромб з тупим кутом 120 . Менша діагональ призми дорівнює 20 см і утворює з площиною основи кут 60 .
Обчислити площу повної поверхні та об’єм прямої призми, основа якої ромб з гострим кутом 60 . Більша діагональ призми дорівнює 24 см і утворює з площиною основи кут 45 .
Знайти площу бічної поверхні та об’єм прямокутного паралелепіпеда діагональ якого дорівнює 10√3 дм і утворює з площиною основи 60 , а одна із сторін основи дорівнює 5 см.
Знайти площу бічної поверхні та об’єм прямокутного паралелепіпеда діагональ якого дорівнює 5√2 дм і утворює з площиною основи 45 , а одна із сторін основи дорівнює 4 см.
В основі прямої призми лежить рівнобедрений трикутник з основою 16 см і бічною стороною 17 см. Діагональ бічної грані, що містить основу трикутника, утворює з площиною основи кут 30 . Обчислити площу повної поверхні та об’єм прямої призми.
Обчислити площу повної поверхні та об’єм прямої призми, основа якої рівнобедрений прямокутний трикутник з гіпотенузою 8 дм. Діагональ найбільшої грані утворює з площиною основи кут 60 .