Типовые примеры Пример 1.
Имеются данные по группе промышленных предприятий за год (таблица 4):
Таблица 4
Данные по промышленным предприятиям
-
№ предприятия
Объем продукции, млн. руб.
Среднегодовая стоимость основных фондов, млн. руб.
Прибыль,
тыс. руб.
1
19,8
10
13,5
2
59,2
24
136,2
3
46,6
19
97,6
4
29,6
12
44,4
5
58,5
22
146,0
6
48,2
20
110,5
7
57,9
21
138,7
8
20,6
9
30,6
9
46,8
19
111,8
10
29,2
14
49,7
11
42,4
18
105,8
12
19,3
9
30,7
13
36,1
14
64,8
14
21,1
10
33,3
15
39,5
16
67,2
Провести группировку по стоимости основных фондов, выделив 3 группы с равными интервалами. Каждую группу охарактеризовать стоимостью основных фондов, выпуском продукции, прибылью, числом предприятий. Рассчитать все вышеназванные показатели в среднем по группам, а также фондоотдачу (выпуск продукции / стоимость основных фондов) и рентабельность основного капитала (прибыль / стоимость основных фондов*100). Сделать выводы.
Решение:
Определим ширину интервала
млн.
руб., (3)
где xmax, xmin – максимальное и минимальное значения кредитных вложений.
Определим теперь интервалы групп (xi, xi+1):
1 группа: 9 – 14 млн. руб.; 2 группа: 14 – 19
млн. руб.; 3 группа: 19 – 24 млн. руб.; где
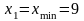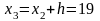млн.
руб.;
млн.
руб.;
млн.
руб.;
млн.
руб.;
Далее упорядочим исходную таблицу по возрастанию основных фондов и выделим группы, в которые попадут предприятия (таблица 5):
Таблица 5
Рабочая таблица группировки
Группы |
№ предприятия |
Объем продукции, млн. руб. |
Среднегодовая стоимость основных фондов, млн. руб. |
Прибыль, тыс. руб. |
1 |
2 |
3 |
4 |
5 |
9 –14 |
1 |
19,8 |
10 |
13,5 |
4 |
29,6 |
12 |
44,4 |
|
8 |
20,6 |
9 |
30,6 |
|
12 |
19,3 |
9 |
30,7 |
|
14 |
21,1 |
10 |
33,3 |
|
Итого |
5 |
110,4 |
50 |
152,5 |
14–19
|
10 |
29,2 |
14 |
49,7 |
11 |
42,4 |
18 |
105,8 |
|
13 |
36,1 |
14 |
64,8 |
|
15 |
39,5 |
16 |
67,2 |
|
Итого |
4 |
147,2 |
62 |
287,5 |
19–24 |
2 |
59,2 |
24 |
136,2 |
3 |
46,6 |
19 |
97,6 |
|
5 |
58,5 |
22 |
146 |
|
6 |
48,2 |
20 |
110,5 |
|
7 |
57,9 |
21 |
138,7 |
|
9 |
46,8 |
19 |
111,8 |
|
Итого |
6 |
317,2 |
125 |
740,8 |
По итоговым данным из рабочей таблицы построим аналитическую группировку, рассчитав все показатели в среднем по группам, а также другие необходимые показатели. Результаты представлены в таблице 6.
Таблица 6
Аналитическая группировка промышленных предприятий
Группы |
Число предприятий |
Объем продукции, млн. руб. |
Стоимость основных фондов, млн. руб. |
Прибыль, тыс. руб. |
Фондоотдача, руб./руб. |
||||
итого |
в среднем |
итого |
в среднем |
итого |
в среднем |
||||
9-14 |
5 |
110,4 |
22,1 |
50 |
10,0 |
152,5 |
30,5 |
2,2 |
|
14-19 |
4 |
147,2 |
36,8 |
62 |
15,5 |
287,5 |
71,9 |
2,4 |
|
19-24 |
6 |
317,2 |
52,9 |
125 |
20,8 |
740,8 |
123,5 |
2,5 |
|
Как видно из таблицы 3, с ростом стоимости основных фондов в среднем по группам увеличиваются – объём произведенной продукции в среднем по группам, прибыль в среднем по группам, а также увеличивается фондоотдача основных фондов. Следовательно, между этими показателями и стоимостью основных фондов существует прямая корреляционная взаимосвязь.
Пример 2.
Имеется информация о количестве книг, полученных студентами по абонементу за прошедший учебный год.
2 4 4 7 6 5 2 2 3 4 4 3 6 5 4 7 6 6 5 3 2 4 2 3 5 7 4 3 3 2 4 5 6 6 10 4 3 3 2 3
Построить вариационный дискретный ряд распределения, обозначив элементы ряда, изобразить его графически.
Решение.
Выделяют две формы вариационного ряда: дискретный ряд и интервальный ряд. Дискретным вариационным рядом распределения называется ранжированная совокупность вариантов хi с соответствующими им частотами. Дискретный вариационный ряд для исходной выборки приведен в таблице 7.
Таблица 7
Дискретный ряд распределения выданных книг
-
Количество выданных книг
хi
Число студентов, получивших книги
fi
2
7
3
9
4
9
5
5
6
6
7
3
10
1
Итого
50
Построим график полигона частот (рисунок 1).
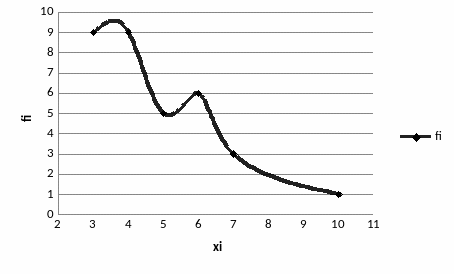
Рис. 1 – Полигон распределения количества выданных книг
в библиотеке
Пример 3
Имеются данные о стоимости основных фондов у 50 предприятий, тыс. руб.:
18,8 16,0 12,6 20,0 30,0 16,4 14,6 18,4 11,6 17,4 10,4 26,4 16,2 15,0 23,6 29,2 17,0 15,6 21,0 12,0 10,0 13,6 16,6 15,4 15,8 18,0 20,2 16,0 24,0 28,0 16,4 19,6 27,0 24,8 11,0 15,8 18,4 21,6 24,2 24,8 25,8 25,2 13,4 19,4 16,6 21,6 30,0 14,0 26,0 19,0
Построить интервальный ряд распределения, выделив 5 групп предприятий (с равными интервалами).
Решение:
Определим размах выборки: R = x max − x min = 30 −10 = 20. Отсюда величина интервала группирования равна h = 20 /5 = 4 Построим ряд распределения, т.е. все данные распределим по сформированным группам (таблица 8).
Таблица 8
Интервальный ряд распределения предприятий по
стоимости основных фондов
Стоимость основных фондов, млн. руб. хi |
Число предприятий fi |
10-14 |
9 |
14-18 |
16 |
18-22 |
11 |
22-26 |
8 |
26-30 |
6 |
Итого |
50 |
Приведем гистограмму распределения стоимости основных фондов (рисунок 2).
Рис. 2 – Гистограмма распределения предприятий по стоимости
основных фондов
Пример 4 Имеется группировка работников предприятия по доходу за октябрь (таблица 9).
Таблица 9
Группировка работников по доходу
Группы работников по доходу, руб. |
Число работников, чел. fi |
До 400 400-1000 1000-1800 1800-3000 3000-4000 4000 и более |
16 20 44 74 37 9 |
ИТОГО: |
200 |
На основе этой группировки построить вторичную группировку с другими интервалами.
Решение:
При построении новых групп на основе имеющихся единицы из старых групп перераспределяются по новым группам пропорционально ширине старых интервалов групп, попавших в новые. Например, новая группа с границами до 500 руб. Складывается из первой старой группы полностью (до 400 руб.) и 1/6 части интервала второй группы ((400-500) составляет 1/6 от (400-1000)). Следовательно, единицы из старой первой и второй группы перераспределяются пропорционально. Остальные новые группы строятся аналогично (таблица 10).
Таблица 10
Вторичная группировка работников по доходу
Группы работников по доходу, руб. |
Число работников, чел. fi |
Расчет |
До 500 500-1000 1000-2000 2000-3000 более 3000 |
19 17 56 62 46 |
16 + 1/6 * 20 = 19 20 – 3 =17 44 + 1/6 * 74 = 56 74 – 12 = 62 37 + 9 = 46 |
ИТОГО: |
200 |
|