2. Свойства σ 2 и σ, формулы их расчета, вариация альтернативного признака

Свойства:

1. Дисперсия и СКО σ ² и σ – постоянной величины = 0.

2. Если все значения признака (x_i) уменьшить или увеличить на число а, то дисперсия и СКО σ ² и σ не изменятся.

3) Если все значения признака (x_i) умножить или разделить на число k, то σ ² изменится в k ² раз, а σ – в k раз.

На основе этих свойств строится упрощенная формула расчета дисперсии и СКО.

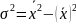(44)

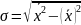(45)

Для нормального закона распределения для показателей вариации существует взаимосвязь.

R ≈ 6 · σ

σ = 1,25· l

На основе СКО можно оценить асимметрию распределения по ряду распределения. Для этого применяется коэффициент асимметрии, который можно найти по формуле

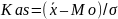(46)

K_as находится в интервале от -3 до 3. Чем ближе к 0, тем асимметрия слабее, чем ближе по модулю к 3, тем сильнее. Если K_as > 0, то асимметрия правосторонняя, если K_as < 0, то левосторонняя.

Альтернативным в статистике считают атрибутивный признак, который может иметь только два значения. Если этот признак у единицы совокупности есть, то он равен 1, если нет, то он равен 0.

Определяется доля единиц, имеющих признак во всей совокупности: p = m/n, где m-это количество единиц, имеющих признак; n-это количество всех единиц.

q = 1– p - это доля единиц, у которых нет признака. Тогда распределение единиц совокупности по альтернативному признаку будет иметь вид:

xi	1	0
fi	p	q

Дисперсия и СКО альтернативного признака находятся по формулам

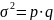(47)

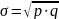
6.3 Виды дисперсий. Правило сложения дисперсий

Вариация признаков в совокупности складывается под влиянием различных внешних и внутренних причин и факторов. Влияние некоторых из этих факторов можно изучить, проведя аналитическую группировку совокупности по этому фактору. По проведенной группировке рассчитываются различные виды дисперсий:

1) Общая дисперсия – характеризует всю вариацию, складывающуюся под влиянием всех факторов.

(48)

2) Межгрупповая дисперсия – характеризует вариацию, складывающуюся под влиянием только группировочного признака.

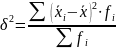(49)

где 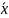– общая средняя для всей совокупности;

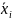– групповые средние;

f_i – количество единиц в группах.

3)Внутригрупповая дисперсия – характеризует вариацию, складывающуюся под влиянием всех других факторов, кроме группировочного. Их будет столько, сколько групп в проведенной группировке.

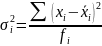(50)

Средняя из внутригрупповых дисперсий равна:

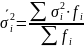(51)

Правило сложения дисперсий

(52)

Общая дисперсия равна сумме межгрупповой и средней из внутригрупповых дисперсий.

Сравнение различных видов дисперсий позволяет изучить влияние группировочного фактора на вариацию изучаемого показателя. Для этого применяют эмпирический коэффициент детерминации (ŋ²).

ŋ² = ∂² / σ ² · 100% (53)

Чем больше доля межгрупповой дисперсии в общей, тем сильнее влияние группировочного фактора на общую вариацию.

Для изучения тесноты взаимосвязи между группировочным фактором и результативным признаком, рассчитанным по группам ( в результате аналитической группировки), применяется эмпирическое корреляционное отношение (ŋ)

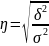(54)

Для того, чтобы сделать вывод по значению ŋ о тесноте взаимосвязи используются соотношения Чеддока (таблица 40).

Таблица 40

Соотношения Чеддока

ŋ	Теснота связи
0-0,3	нет связи
0,3-0,5	слабая
0,5-0,7	умеренная
0,7-0,9	тесная
0,9-1,0	очень тесная
1	функциональная