Типовые примеры
Пример 1.
Известны данные по фирме о выпуске экспортной продукции за год (таблица 27).
Таблица 27
Данные по производству трех видов продукции на экспорт
-
Вид продукции
Стоимость продукции на экспорт, тыс. руб.
Удельный вес продукции на экспорт от всей продукции, %
Стоимость всей продукции, тыс. руб.
wi
xi
wi / xi *100
Сталь
320
40
800
Прокат
420
35
1200
Итого
740
-
2000
Определите средний удельный вес продукции на экспорт по предприятию.
Решение:
Составим логическую формулу средней величины (экономическое содержание).
Средний удельный вес Стоимость продукции на экспорт
продукции на экспорт = _______________________________ * 100 . (36)
Стоимость всей продукции
Так как по исходным данным известен числитель логической формулы и не известен знаменатель, то для расчетов данной средней величины будем применять среднюю гармоническую взвешенную. Неизвестные данные рассчитаем в таблице 4.
Таким образом, средний удельный вес экспортной продукции предприятия
Пример 2.
Имеются данные распределения домохозяйств по уровню среднедушевого дохода. Результаты обследования представлены в таблице 28.
Таблица 28
Распределение домохозяйств по уровню среднедушевого дохода
Среднедушевой доход , руб. |
До 200 |
200 -400 |
400 –600 |
600 –800 |
800 - 1000 |
1000 - 1200 |
1200 и более |
Число домохозяйств |
5 |
12 |
24 |
56 |
80 |
15 |
8 |
Определить среднедушевой доход на 1 домохозяйство методом моментов.
Решение: Для расчетов построим расчетную таблицу 29.
Таблица 29
Расчетная таблица
Среднедушевой доход, руб. |
Число домохозяйств fi |
Середина xi |
xí = (xi – A)/k = = (xi – 900)/200 |
xí *fi |
До 200 |
5 |
100 |
-4 |
-20 |
200-400 |
12 |
300 |
-3 |
-36 |
400-600 |
24 |
500 |
-2 |
-48 |
600-800 |
56 |
700 |
-1 |
-56 |
800-1000 |
80 |
900 (A) |
0 |
0 |
1000-1200 |
15 |
1100 |
1 |
15 |
1200 и более |
8 |
1300 |
2 |
16 |
Итого |
200 |
- |
- |
-129 |
Преобразуем исходные данные (колонка 4 расчетной таблицы).
Средняя для преобразованных данных равна
Средняя для исходных данных равна
Таким образом, среднедушевой доход на 1 домохозяйство равен 771 руб.
Пример 3
Имеются данные распределения предприятий по численности промышленно-производственного персонала (таблица 30).
Таблица 30
Группировка предприятий по числу работающих
Число работающих, чел. |
100-200 |
200-300 |
300-400 |
400-500 |
500-600 |
600-700 |
700-800 |
Число предприятий |
1 |
3 |
7 |
30 |
19 |
15 |
5 |
Определить среднюю, моду, медиану и сделать выводы.
Решение: Для расчетов построим расчетную таблицу 31.
Таблица 31
Расчетная таблица
-
Численность работников
Число предприятий,
fi
Середина
xi
xi*fi
fiнакопл
100-200
1
150
150
1
200-300
3
250
750
4
300-400
7
350
2450
11
400-500
30
450
13500
41
500-600
19
550
10450
60
600-700
15
650
9750
75
700-800
5
750
3750
80
Итого
80
-
40800
-
Средняя численность работников по совокупности составила
Определим моду и медиану. Мода находится в интервале (400-500), так как в нем наблюдается максимальная частота.
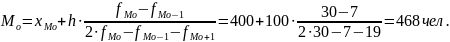
Медиана находится в интервале (400-500), так как накопленная частота в нем превышает половину единиц совокупности.
Вывод:
Средняя численность по всем предприятиям
равна 510 чел., наиболее часто встречаются
предприятия с численностью 468 чел.,
половина предприятий имеют численность
менее 497 чел., а вторая половина более.
Так как выполняется неравенство
,
то
распределение предприятий по численности
имеет правостороннюю асимметрию.
Пример 4. По коммерческой фирме имеются данные о величине запасов на 1-е число каждого месяца (таблица 32).
Таблица 32
Товарные запасы по фирме за полугодие
Даты |
01.01. |
01.02 |
01.03. |
01.04. |
01.05. |
01.06. |
01.07 |
Товарные запасы, тыс. руб. |
100 |
120 |
125 |
130 |
128 |
115 |
110 |
Определите средние товарные запасы за 1 и 2 кварталы и процент изменения запасов.
Решение:
Определим средние товарные запасы за 1 квартал по средней хронологической простой:
2. Определим средние товарные запасы за 2 квартал по средней хронологической простой:
Процент изменения среднеквартальных запасов определим по формуле
Следовательно, средние товарные запасы во втором квартале увеличились на 0,83%.