17 Оптимальность движения поезда и ее ограничения

Расчет скорости движения поезда, изложенный ранее, производили при условии заданной массы не меньший практический интерес представляет решение обратной задачи-определения массы поезда при условии заданной нормативной скорости движения труднейшем на элементе профиля пути Если в первом случае использовались возможности локомотива по быстродействию, то во втором по тяге однако решение обеих задач в совокупности должно быть оптимальны скорости является основным способом интенсификации железнодорожного транспорта в условиях непрерывного роста объема перевозок и высокой грузонапряженности. ясно. что оптимизация массы и скорости поездов является обще транспортной проблемой. Ее решение начинают с тяговых расчетов, методика которых построена на основе системного подхода и принципа максимума для того чтобы обеспечить наибольшую провозную способность линии, масса поезда должна быть максимальной за счет полного использования силы тяги и мощности локомотива, кинетической энергии поездов и рациональной организации использования тяговых средств при гарантирован ной безопасности движения и надежности работы мотивного парка. С этих позиции ПТР устанавливают нормативные значения расчетных силы тяги и скорости на труднейших подъемах максимально допустимых токов по коммутации, температур нагревания обмоток и кое фициентов сцепления движущих колес с рельсами мя различных серий локомотивов. Если рельсы являются удерживающими связями, ограничиваюшими свобод, движения, то расчетно-нормативные параметры являют ей управляющими связями, ограничивающими режимы и состояния локомотивов по их тягово-энергетическим ресурсам и по эксплуатационной надежности. Но если первые действуют постоянно и жестко. то вторые необходимо учитывать в расчетах так, чтобы не допустить состояний на пределе этих ограничений обеспечивает полное использование силы тяги мощности локомотивов для вождения поездов наибольшей массы для расчета массы составов чаще всего таким ограничением является сила тяги по сцеплению тепловозы обычно имеют избыточный сцепной вес и в таких случаях ограничение расчетной силы тяги устанав ливается по дизелю. Эти ограничения и определяют расчетно-нормативные значения силы тяги Fk и скорости V для каждой серии локомотивов, по которым определяется масса состава на расчетном или инерционном подъеме

Расчетным называют наиболее крутой и затяжной подъем на участке, на котором при движении устанавливается равномерная скорость равная расчетной скорости локомотива заданной серии Инерционным или скоростным называют подъем наибольшей крутизны на тяговом участке и сравнительно небольшой протяженности, преодоление которого при движении скоростью становится возможным благодаря использованию кинет ческой энергии поезда, накопленной перед входом на этот подъем.

Методика расчета массы поезда зависит от характера профиля пути При наличии явно выраженного затяжного подъема большой крутизны массу когда на участке имеется подъем более крутой, чем расчетный но небольшой проmяженности то сначала массу поезда определяют по крутизне расчетного подъема, а возможность более крутого прохождения го проверяют с учетом использования кинетической энергии поезда При этом скорость движения в конце этого подъема должна быть иже расчетной Если это условие не выполняется то предполагаемый инерционный подъем следует признать расчетным и массу поезда определить с расчетной скоростью на этом подъеме.

При расчете массы составов с учетом использования кинетической энергии поезда используют ту же методику, что и при решении прямой линеаризация функции v(s) и t(s) принцип малых отклонений управляющих и возмущающих сил, использование начальных условий в форме задачи о наблюдаемости. После определения массы состава таким методом производят проверочные расчеты ее соответствия эксплуатации, технологии перевозок, надежности тяги безопасности движения.

Ограничения массы поезда по у с л о в и я м эксплуатации и надежности тяги могут возникнуть вследствие. ной длины приемоотправочных путей раздельных пунктов и установки на них поезда, масса которого определена по расчетном превышения допустимого перегрева обмоток двигателей: 1 коммутации тока двигателей, нестандартных метеорологических условий низкой температуры воздуха, пониженного атмосферного давления, сильного ветра, недостаточной силы тяги для трогания с разгона поезда на станции перед выходом на подъем большой кр недостаточной прочности автосцепных приборов, неустойчивости вагонов при толкании или рекуперативном торможении

По тех н ол о ги чес к и м. усл о в и я м перевозок поездов может изменяться в связи с унификацией массы марш поездов, с вождением тяжеловесных поездов по специальным графика движения, с необходимостью увеличения провозной способности и применением кратной тяги или толкания с приор по скорости поездов различных категорий ускоренные грузовые рефрижераторные); с организацией движения порожних составов регулировке погрузочных ресурсов,

Реализация оптимальных значений массы и скорости движения может быть достигнута при полном соответствии нормативов и 1 свойств локомотивов конкретным условиям их эксплуатации. которые не могут быть одинаковыми на всей сети дорог.

Более того, работы локомотивов, с которыми связана надежность тяги, не определяться: организацией управления движением потока по степенью заполнения пропускной способности линии и неравномерность пропуска по участку сезонным изменением структуры. токов, влияющим на основное сопротивление движению, наконец случайными факторами(не поддающимися измерению)

18.Аналитический метод. Для расчета движения поезда, необходимо вначале определить удельную равнодействующую силу, которую обозначим f_у . Допустим, что ее диаграмма построена (рисунок 7.1). Для использования принципа малых отклонений произведем кусочно-линейную аппроксимацию диаграммы, руководствуясь правилами линеаризации. С этой целью разобьем ось абсцисс на интервалы скоростей

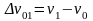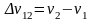, и т.д.

Найдем средние скорости в каждом интервале:

и …

и 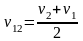соответственно им определим по диаграмме равнодействующие сил f_у01, f_у12 и т. д. Принимаем силы постоянными в интервалах и на этом основании получим кусочно-линейную зависимость f_у (v) (штриховая линия на рис. 7.1). Результаты аппроксимации используем для решения дифференциального уравнения движения.

Практический интерес представляют зависимости времени движения в функции скорости t(v),пройденного пути в функции скорости S(v), пройденного пути в функции времени S(t). Произведем интегрирование с целью получения этих зависимостей.

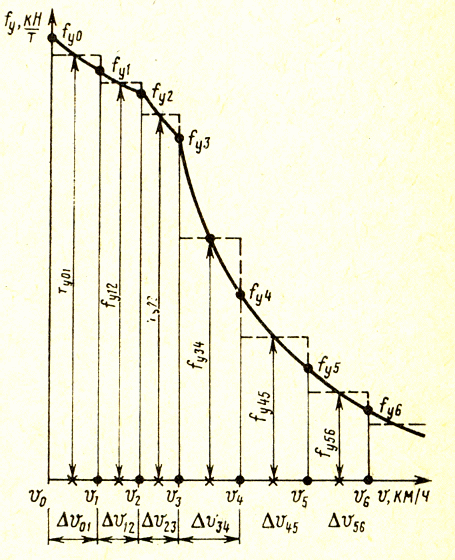
Рисунок 7.1. Кусочно-линейная

аппроксимация равнодействующих сил поезда в режиме тяги

Интегрирование уравнения движения по времени и скорости. Возьмем интервал скорости в начале движения поезда 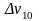и в его пределах найдем на диаграмме равнодействующую сил f_{у01 .} Произведем перестановки переменных уравнения (7.1) и вынесем за знак интеграла подынтегральную функцию 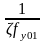на том основании, что в пределах интервала скорости она принята постоянной. Напишем уравнение движения в форме определенного интеграла:

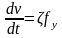(7.1)

.

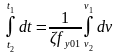Выражая скорость в км/ч, а равнодействующую силу в Н/кН и интегрируя уравнение движения, получим выражение для определения времени движения поезда:

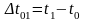
Если ζ= 122,4 км/ч² /(Н/кН) то время движения в мин

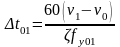. (7.2)

По этим формулам можно определить время, которое потребуется для увеличения скорости поезда от v₀ до v_n .

Lля того чтобы ввести путь в уравнение движения, умножим и разделим на левую часть уравнения:

, откуда (7.3)

После перестановки переменных получим 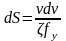. Возьмем интеграл скорости в начале движения от v₀ до v_n , определим среднюю скорость и на диаграмме равнодействующих сил найдем ей соответствующую силу f_у01.

После интегрирования уравнения (7.3) получим путь, пройденный поездом при измерении скорости от v₀ до v₁ в м

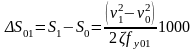. (7.4)

Подобным образом определим пройденный путь 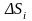для последующих интервалов скоростей и суммированием найдем путь S, пройденный поездом при возрастании скорости от v₀ до v_n.

Общее решение уравнения движения поезда во всем диапазоне скоростей определяется как сумма частных решений, т.е.

, .

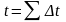Решение уравнения движения поезда аналитическим способом удобней производить в табличной форме (таблица 7.1)