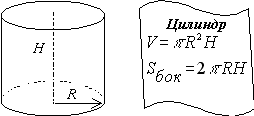6. Коло, круг

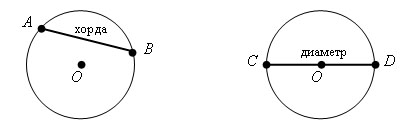
Коло – множина точок площини, відстань яких від даної точки (центра кола) дорівнює даній відстані (радіусу кола).

Радіус кола – відстань від центра кола до точки кола (відрізок, що з’єднує центр кола з точкою кола). ОD – радіус.

Хорда кола – відрізок, що з’єднує дві точки кола. AВ – хорда.

Діаметр кола — хорда, яка проходить через центр кола. CD – діаметр, CD = 2OD.

Круг – множина точок площини, відстань яких від даної точки (центра круга) не перевищує даної відстані (радіуса круга).

Радіус, хорда, діаметр кола, яке обмежує даний круг, називають радіусом круга, хордою круга, діаметром круга.

Питання для узагальнення

• Що називається колом?

• Що називається радіусом кола?

• Що таке хорда?

• Що називається кругом?

7. Многокутники та їх властивості

Чотирикутник – це частина площини, обмежена замкненою ламаною, яка містить чотири ланки. Вона складається з чотирьох вершин (точок) і чотирьох сторін (відрізків), що послідовно їх сполучають. При цьому жодні три з даних точок не повинні лежати на одній прямій. Вершини називаються сусідніми, якщо вони є кінцями однієї з його сторін. Несусідні вершини називаються протилежними. Відрізки, що сполучають протилежні вершини чотирикутника, називаються діагоналями.

Сума кутів чотирикутника дорівнює 360°.

A + В + С + D = 360°.

Кожна сторона чотирикутника менша за суму усіх його інших сторін.

А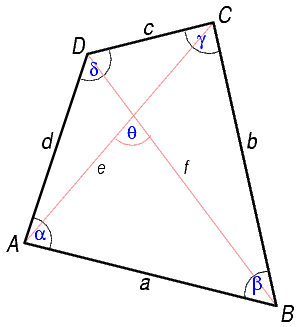 В < АD + ВС + СВ.

П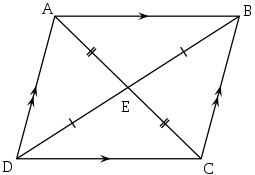 аралелограм – це чотирикутник, протилежні сторони якого попарно паралельні.

Існує декілька окремих видів паралелограмів:

Прямокутник – паралелограм, всі кути якого прямі.

Ромб – паралелограм, всі чотири сторони якого рівні.

Квадрат – рівносторонній прямокутник або прямокутний ромб.

Властивості паралелограма:

1. Протилежні сторони паралелограма рівні, тобто АВ = DC та AD = BC.

2. Протилежні кути паралелограма рівні, тобто А = С та В = D.

3. Діагоналі паралелограма перетинаються та в точці перетину діляться навпіл.

4. Сума сусідніх кутів дорівнює 180^̊, загальна сума кутів паралелограма дорівнює 360^̊.

5. Сума квадратів діагоналей дорівнює подвоєній сумі квадратів його сторін.

Властивості квадрата:

1. У 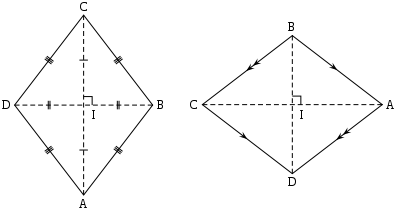квадрат завжди можна вписати коло.

2. Навколо квадрату завжди можна описати коло.

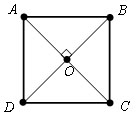
Властивості ромба:

1. Діагоналі ромба перетинаються під прямим кутом.

2. Діагоналі ромба є бісектрисами кутів, з яких вони проведені.

Питання для узагальнення

• Що називається чотирикутником?

• Чому дорівнює сума кутів чотирикутника?

• Який чотирикутник називається паралелограмом?

• Що таке прямокутник? Квадрат? Ромб?

• Які властивості має паралелограм?

8. Многогранники і тіла обертання

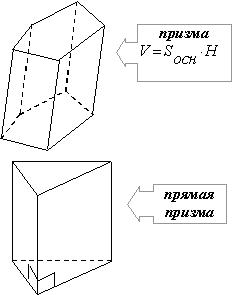
	Означення. п-кутна призма – многогранник, дві грані якого п- кутники, що лежать у різних площинах і суміщаються паралельним перенесенням, а інші п граней – паралелограми. n-кутники називають основами призми, а паралелограми – бічними гранями призми. Сторони основ називають ребрами основ, інші ребра називають бічними ребрами. Висота призми – відстань між площинами її основ. Діагональ призми – відрізок, який сполучає дві вершини, що не належать одній грані.
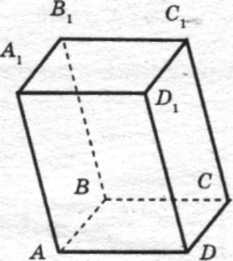
	Означення. Паралелепіпед – призма, основа якої паралелограм. АВСDА1В1С1D1 – паралелепіпед. Протилежні грані паралелепіпеда – грані паралелепіпеда, які не мають спільних вершин
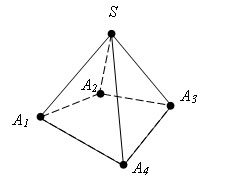
	Означення. n-кутна піраміда – многогранник, у якого одна грань – довільний n-кутник, а останні n граней – трикутники, що мають спільну вершину, n-кутник називають основою, трикутники – бічними гранями, а спільну вершину бічних граней – вершиною піраміди. SA1A2A3A4 – піраміда, A1A2A3A4 – основа; SA1A2, SA2A3, SA3A4, SA1A4 – бічні грані; S – вершина піраміди.
	Висота – перпендикуляр, опущений з вершини піраміди на площину основи.
	Означення. Циліндром називається тіло, що складається з двох кругів, які не лежать в одній площині і суміщаються паралельним перенесенням, і всіх відрізків, що сполучають відповідні точки цих кругів. Круги називаються основами циліндра, а відрізки, що сполучають точки кіл кругів, – твірними циліндра. Відстань між площинами основ називається висотою циліндра.
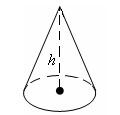
	Означення. Конусом називається тіло, яке складається з круга – основи конуса, точки, яка не лежить у площині цього круга – вершини конуса і всіх відрізків, що сполучають вершину конуса з точками кола основи. Відрізки, що сполучають вершину конуса з точками кола основи, називаються твірними конуса. Висота – перпендикуляр, опущений з вершини конуса на площину основи.
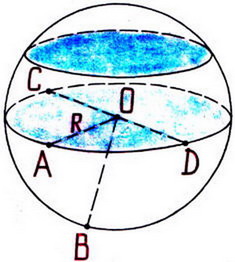
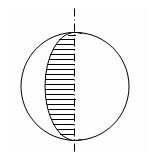
	Означення. Кулею називається тіло, що складається з усіх точок простору, які знаходяться від даної точки на відстані, не більшій за дану. Ця точка називається центром кулі, а дана відстань радіусом кулі. Куля є тілом обертання. Вона утворюється під час обертання півкруга навколо його діаметра як осі.
	Межа кулі називається кульовою поверхнею або сферою.

Питання для узагальнення

• Що називається призмою?

• Яке тіло називається кулею?

• Що називається паралелепіпедом?

• Яке тіло називається циліндром?

3. Заключна частина

Загальний висновок

Геометрія вивчає геометричні фігури та їх властивості.

Геометрія поділяється на:

• планіметрію (вивчає площинні фігури, тобто ті фігури, які можна накреслити на папері, вирізати та повністю розташувати на папері, або прикласти до дошки, або наклеїти на картон);

• стереометрію (вивчає просторові тіла, фігури, які не можна повністю розташувати на площині).