Министерство образования и науки Российской Федерации

КАЗАНСКИЙ (ПРИВОЛЖСКИЙ) ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Институт математики и механики кафедра аэрогидромеханики

Специальность: 010200 – механика

Специализация: аэрогидромеханика

ВЫПУСКНАЯ КВАЛИФИКАЦИОННАЯ РАБОТА

(Бакалаврская работа)

ПРИТОК ЖИДКОСТИ К СКВАЖИНЕ ПРИ ЧАСТИЧНО ИЗОЛИРОВАННОМ КОНТУРЕ ПИТАНИЯ

Работа завершена:

"___" __________ 201_ г. ____________________ (Чечинова А. Г.)

Работа допущена к защите:

Научный руководитель

доц. каф. аэрогидромеханики

к.ф.-м.н. Поташев К.А.

"___" __________ 201_ г. ____________________ (Поташев К. А.)

Заведующий кафедрой

проф. Егоров А. Г.

"___" __________ 201_ г. ____________________ (Егоров А. Г.)

Казань – 2013

Оглавление

Y

Введение 3

Постановка задачи 4

1. Связь плоской задачи теории фильтрации с теорией функции комплексного переменного 5

1.1 Построение комплексных областей 5

1.2 Нахождение комплексного потенциала 6

1.3 Вычисление дебита скважины 9

2. Результаты 12

3. Исследование дебита при разных углах 14

3. Исследование скорости жидкости внутри пласта 16

5. Динамика контурного фронта 19

6. Оценка коэффициента извлечения нефти 24

Заключение 28

Литература 29

Введение

В сборнике задач по подземной гидравлике [1] приводится задача по определению дебита скважины при частично изолированном контуре питания и заданном давлении на контуре питания и на забое скважины. Продемонстрировано решение задачи путем сведения к плоскорадиальной, принимая за контурное давление в формуле Дюпюи средневзвешенное исходное давление по всей длине окружности. В настоящей работе подробно исследуется движение жидкости внутри частично ограниченного кругового пласта и оцениваются пределы применимости указанного способа решения.

Постановка задачи

Скважина радиуса расположена в центре кругового пласта радиусом (рис.1). Залежь по контуру частично непроницаема. Контур питания представляет собой в плоскости дугу окружности радиуса с центральным углом . Давление на контуре питания равно – , давление на забое скважины равно – . Граница изолирована. Требуется определить дебит скважины в данных условиях, исследовать распределение скоростей внутри пласта, а также проследить динамику продвижения контурного фронта к скважине. Задача будет рассматриваться при разных углах .

Рис. 1 Схема частично изолированного кругового пласта, вскрытого скважиной

1. Связь плоской задачи теории фильтрации с теорией функции комплексного переменного

При исследовании плоского фильтрационного потока, подчиняющегося закону Дарси, можно использовать теорию комплексного переменного. Совместим плоскость комплексного переменного с основной плоскостью течения.

Для каждого плоского фильтрационного потока можно найти комплексный потенциал , который является функцией комплексного переменного :

где – потенциал скорости; – функция тока, линии постоянного давления.

1. Построение комплексных областей

Для нахождения комплексного потенциала нужно отобразить область круга на полубесконечную полосу, рассматривая скважину как точечный источник или сток.

Точки области отображаются на область , как показано на рис.2.

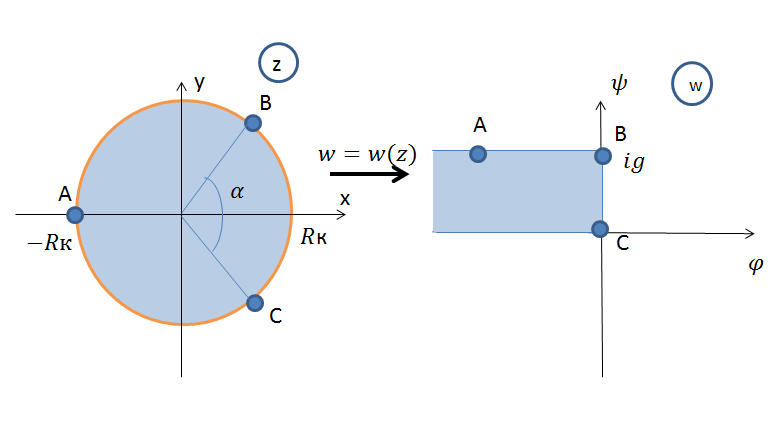
Рис. 2 Отображение круговой области пласта на полубесконечную полосу

Величина пока неизвестна.